CHAPTER 3

VECTORS

• physical quantities identified by a single number are called scalars (e.g. mass, temperature, time interval, etc.)
• quantities fully specified by a number and a direction are called vectors (e.g. displacement, velocity, force, electric field, etc.)

Vector Operations: sum, difference, multiplication. Graphic procedure


vector components

While graphical procedures are very useful in providing a visual understanding of any operation among vectors, more precise numerical results can be obtained by operating upon the vector's components.

For a given choice of (two-dimensional) reference frame (xy), the vector components are given by the projection of the vector on the two axes. If a vector has magnitude V and it makes an angle 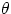$\theta$ with the x-axis, then

$V_{x} = V\cos\theta$

$V_{y} = V\sin\theta$

Conversely, one also has

$V = \sqrt{V_{x}^{2}+V_{y}^{2}}$

$\tan\theta = V_{y}/V_{x}$

NOTE:

1.

in a two-dimensional space, a vector is fully identified by two numbers. These can be either

(a)

the magnitude and the angle, or

(b)

the numerical values of the two components

In a three-dimensional space, a vector is identified by three numbers, either its three components or the magnitude and two angles (or some other suitable choice of quantities). In an n-dimensional space, vectors will have n components (in relativity, one works in a 4-dimensional space, with 3 space components and one time component)

2.

the numerical values of a vector's component depend upon the choice of the frame of reference. In any given problem, one is free to choose the orientation of the x,y,z, axes in any suitable way. The choice of axes will determine the values of the components, but will not affect the vector's magnitude.

Operations among vectors: numerical procedures

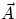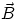If $\vec{A}$ and $\vec{B}$ are two vectors, and 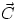$\vec{C}$ their sum, 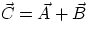$\vec{C}=\vec{A}+\vec{B}$, then

C_x = A_x+B_x

C_y = A_y+B_y

the components of the sum-vector are given by the sum of the components
Unit Vectors Properly speaking, components are not vectors but scalars. But it is often useful to think in terms of a vector whose magnitude is the actual value of the component. This is done by introducing the unit vectors, i.e. vectors of magnitude 1 and directions parallel to the reference axes x,y,z. Calling such vectors 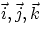$\vec{i}, \vec{j}, \vec{k}$, one has

$\vec{A_{x}} = A_{x}\vec{i}$

$\vec{A_{y}} = A_{y}\vec{j}$

$\vec{A_{z}} = A_{z}\vec{k}$

and also

$\vec{A} = \vec{A_{x}}+ \vec{A_{y}} + \vec{A_{z}}$