


Next: About this document ...
CHAPTER 4
Kinematics in 2 dimensions
When dealing with motions in two (or more) dimensions, it is necessary to take into account the
vector nature of the variables we have encounterd so far. Specifically:
- the position of an object in the xy plane (or the xyz space) is given by a vector
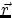 going from the origin to the object's location
going from the origin to the object's location
- the displacement between two positions 1 and 2 will be the vector difference
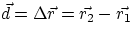 .
. - average velocity is, as before, given by
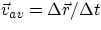 , while the
instantaneous velocity is
, while the
instantaneous velocity is 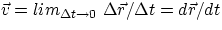 .
. - similarly, average and instantaneous accelerations will be
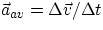 and
and 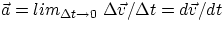 .
.
(Note : velocity being a vector, it is characterized by both a magnitude and a direction. Therefore
velocity will change if either its magnitude or its direction (or both) do change. As changes in
velocity are associated with accelerations, we conclude that accelerations are present even
when a body only changes its direction while maintaining a constant speed.)
As a next step, we can rewrite the equations of motion :
- 1.
- motion with constant velocity
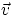 :
:
- 2.
- motion with constant acceleration
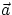 :
:
This is all very nice, but how can we handle vector equations ?
Not easily, in fact the best (only?) way to handle them is by operating separately on the x and y
(and z) projections.
For instance, the constant velocity equation is equivalent to
x(t) = x0 + vxt
y(t) = y0 + vyt
where x0, y0, vx, vy are respectively the components of 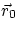 ,
, 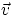 .
.
When dealing with a two-dimensional motion, in addition to the (x vs. t) and (y vs. t) expressions, one can
also (by solving for t in one expression and substituting in the other) obtain an expression for the
object's trajectory, i.e. the y vs. x curve.
In the case of constant 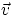 , one obtains for the trajectory
, one obtains for the trajectory
y = y0 + vy/vx(x-x0)
which represents a straight line in the xy plane of slope 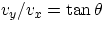 , where
, where 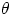 is the
angle the velocity does with the x-axis.
is the
angle the velocity does with the x-axis.
In general, any motion in a two dimensional plane can be thought of as the superposition of two
independent motions in the horizontal and vertical directions. To get the global vectorial quantities at
any time,one needs to study the two motions separately, and then recombine them to obtain the vectors from
their components.
Important case : projectile motion
Here, the two independent motions are a motion with constant velocity in the horizontal direction, and a motion
with constant acceleration g in the vertical direction. In this case the equations of motin are:
x(t) = x0 + v0xt
y(t) = y0 + v0yt + 1/2 gt2
while for the trajectory one would obtain (assuming for simplicity x0 = y0 = 0)
with 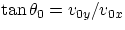 and
and 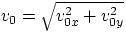 .These equations allow to determine, for any particular situation, range, "air time", maximum height, etc.
.These equations allow to determine, for any particular situation, range, "air time", maximum height, etc.
Uniform Circular Motion:
circular trajectory of radius r with constant speed v.
As the velocity is changing (in direction only, not in magnitude) an acceleration must be present. What are its
magnitude and direction ? As shown in the book, one could prove that
- 1.
- the magnitude of the acceleration is a = v2/r
- 2.
- the direction is always towards the center of the circle, therefore it is referred to as
centripetal ("seeking the center") or radial (directed along the radius)
Note : the derivation given in the book exploits the fact that the two triangles in fig 4.16 are similar. How can we
tell that ? Answer : to prove that 2 triangles are similar, it is enough to show that they have the same angles.
When dealing with isosceles triangles, as is the case here, it is enough to show that one angle is the same. In
figs. 4.16 (b) and (c), the angle 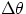 is the same in both triangles since their sides are perpendicular
(radius is always perpendicular to the tangent).
is the same in both triangles since their sides are perpendicular
(radius is always perpendicular to the tangent).
Uniform Circular Motion: the acceleration is constant in magnitude but continuously varying in direction.
In fact its direction is always perpendicular to the direction of the instant velocity.
In the Uniform Circular Motion the acceleration is always perpendicular to the velocity, and it does not affect
the magnitude but only the direction of the velocity. This is quite a general result :
consider an arbitrary two dimensional motion : at a given instant let 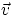 be the velocity and
be the velocity and 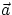 the
acceleration. It will always be possible to resolve
the
acceleration. It will always be possible to resolve 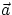 into the components parallel and perpendicular to
into the components parallel and perpendicular to
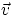 . One could convince oneself that
. One could convince oneself that
- 1.
- the parallel (or tangential) component is only responsible for changing the velocity's magnitude
- 2.
- the perpendicular (or radial) component is only responsible for changing the velocity's direction
Intuitive argument : think of the velocity vector as made of stretchable rubber, fixed at one end but able to
rotate around the fixed point. If the acceleration "pulls" along the direction of 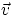 it will stretch it,
while if it "pulls" perpendicularly it will rotate
it will stretch it,
while if it "pulls" perpendicularly it will rotate 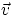 without stretching it......
without stretching it......
The following expressions are valid for any arbitrary motion:
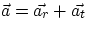 ar
ar =
v2/
r
v,
r = instantaneous velocity and radius of curvature)
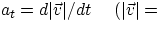
magnitude of
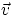
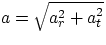
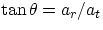
(we will ignore the unit vectors 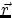 and
and 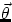 for now, if necessary we will discuss them in the
future).
Relative Velocity
for now, if necessary we will discuss them in the
future).
Relative Velocity
Relativity was invented by Galileo, not by Einstein. Galileo was well aware that displacements, velocities, etc.
are not absolute quantities but depend upon the motion of the observer (Einstein's achievement was bolder : he
showed that not only space, but also time is relative !!).
If you are flying in a jet plane at  400 mph, and throw a peanut in the air, after
400 mph, and throw a peanut in the air, after  1 sec it will
fall back in your hand. But during that second you have advanced by almost 180 meters !! (and so must have done the
peanut). To your eyes, the peanut underwent a purely up and down motion (with 0 horizontal velocity), but to an
eagle soaring in mid-air and watching through the window, the peanut trajectory was a shallow parabola, 180 m long
and 1 m high (Galileo, who hadn't seen jet-planes, used the example of a sailor dropping a mallet from the top of the
mast of a moving ship).
1 sec it will
fall back in your hand. But during that second you have advanced by almost 180 meters !! (and so must have done the
peanut). To your eyes, the peanut underwent a purely up and down motion (with 0 horizontal velocity), but to an
eagle soaring in mid-air and watching through the window, the peanut trajectory was a shallow parabola, 180 m long
and 1 m high (Galileo, who hadn't seen jet-planes, used the example of a sailor dropping a mallet from the top of the
mast of a moving ship).
Formal treatment :
Consider a frame of reference F at rest (with respect to the Earth) , and another frame F' moving with constant
velocity 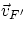 with respect to F. Assume for simplicity that the origins of the two frames coincide at
t=0. The expression relating the coordinates of any point, as measured in the two frames is
(remember:
with respect to F. Assume for simplicity that the origins of the two frames coincide at
t=0. The expression relating the coordinates of any point, as measured in the two frames is
(remember: 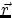 has the coordinates x,y,z as components). The derivative of the above formula gives us an
expression relating the velocity of a given object as measured in the frame F or F':
Vector equations are, as usual, compact and elegant, but to perform any numerical calculation we need to project
them onto the axes. In two dimensions, the expression above is equivalent to
has the coordinates x,y,z as components). The derivative of the above formula gives us an
expression relating the velocity of a given object as measured in the frame F or F':
Vector equations are, as usual, compact and elegant, but to perform any numerical calculation we need to project
them onto the axes. In two dimensions, the expression above is equivalent to
v'x = vx - vF'x
v'y = vy - vF'y
The simpler cases to analyze are obviously when either 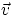 or
or 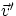 (or both) are parallel to the x
(or y) axis.
(or both) are parallel to the x
(or y) axis.



Next: About this document ...
Sergio Conetti
9/13/2000