


Next: About this document ...
Chapter 5
Newton and 'The Force"
Misconceptions by Aristoteles and followers:
- 1.
- heavier objects fall faster (we have seen how Galileo took care of that)
- 2.
- to keep an object in motion at constant velocity, a constant "agent" is needed
(e.g. horse pulling a cart, wind pushing a sailboat,etc.)
The problem with this second statement was in not realizing that, in
addition to the pulling or pushing agent, there are other agents,
typically friction and air or water resistance, involved in the phenomena mentioned.
If we eliminate such spurious agents, then,
once a body is in motion with a certain velocity, it tends to
maintain it: in ideal, albeit abstract, conditions, it will move forever at the same velocity.
Generalizing this idea, we can state Newton's first law of motion or Law of Inertia :
an object will maintain a state of rest or of motion at constant
velocity unless some external agent intervenes to modify it.
Any such agent that can modify the state of motion of an object is what we
call a Force.
With hindsight, we can quickly realize that there are plenty of
examples of the law of inertia in everyday's life :
- if you (very unwisely) sit in a car without seat
belts, and the driver jams the brakes, you fly against the windshield. Why?
Is anyone throwing you against the shield? No, what is happening is that, while the car is
slowing down, you keep moving with whatever velocity you (and the car) had
- when a car circling a bend encounters an icy patch or an oil slick, it
takes off along the tangent to the curve (i.e. in the direction of its instantaneous
velocity), since the force that kept it on the curved trajectory, i.e. the tire
friction on the ground, stops acting.
- etc.
We then see that a force is something that causes the velocity to change.
By definition, whenever an object changes its velocity, it undergoes an acceleration.
We then infer that there has to be a strict correlation between forces and accelerations.
Can we say more about such a relation? The first obvious
statement is that, the greater the force, the greater the acceleration. Careful measurements
would show that the acceleration is actually proportional to the force.
Moreover, it is equally intuitive that the acceleration (i.e. the change in velocity) will
be in the same direction as the force. We can then write
What else can we say ? We can try applying the same force to different objects, and see
what happens . Obviously a more massive object will be accelerated less than a less massive
one: try to give the same kick to a soccer ball or to a bowling ball.....Or try to stop
(i.e. to change the velocity of) a bowling ball or a soccer ball moving at the same speed...
These considerations allow us to give a quantitative definition to the concept of
mass : the mass of an object is a measure of its inertia, i.e of the resistance a body
opposes to have its state of motion changed. Mass is therefore the "missing link" in the
force vs. acceleration equation, that we can now write
This is Newton's second law of motion, and, in spite of its apparent simplicity and almost
obvious appearance, it has incredibly far-reaching consequences.
Newton's law allows us to define the unit for forces, the newton (N): a force of 1
newton will impart to the mass of 1 kg the acceleration of 1 m/s2. Dimensionally:
[F] = [MLT-2]
Combination of Forces
In general, there can be many different forces applied to a given body and, in order to
obtain the final effect (i.e. the value of the acceleration) one has to consider the
net force, i.e. the (vector) sum of all the forces acting onto the body. Most
obvious example : if I apply two forces which are equal and opposite, their sum will be zero
and no net force will be acting on the body. Does this mean that the object is at
rest?
No, if an object has no net force acting upon it, it will be either at rest
or moving with constant velocity.
We can then conclude :
no net force

constant velocity (possibly =0)
constant velocity (including 0)

no net force
net force

change in velocity
Mass vs. Weight
At this point, it should be clear what we mean by mass. What about weight? We define weight as the force felt by
an object of mass m due to gravity. Therefore
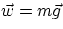
This definition has the following implications :
- weights should be measured in Newtons (or in pounds, as long as we understand that the pound is a unit of force,
not of mass)
- Given that g depends upon the location, the weight of an object is not a costant quantity (while its mass is: mass
is an intrinsic, invariant attribute of any given object).
- the correct way to measure a mass is to give it a known force and measure its acceleration.
- astronauts revolving the earth are not weightless (when trying to be precise, one talks in terms of
apparent weightlessness), since gravity, albeit reduced, is still very much present. Astronauts are "weightless" as
much as you would be if you were standing on bathroom scales in an elevator, and the elevator cable broke: the
scales would record 0, but you still are very much under the effect of gravity (and your weight is still mg...)
- when you exercise heavily and burn off some fat, it is more correct to say that you are losing mass. But of
course, in any given location, if your mass changes, so does your weight.
Newton's third law
Think of pushing on a wall : you are definitely exerting
a force on the wall, but you also feel a pressure on your hand; the wall is
therefore exerting a force on your hand. Similarly, if you kick a ball (think
of kicking a bowling ball with your bare foot), you will feel for sure that,
while you are exerting a force on the ball, the ball gets back at you. These
are all examples of a very general rule, Newton's third Law (also called action
and reaction), that states :
whenever an object A exerts a force on an object B,
B will exert a force
on A
which is equal and opposite to the force exerted by A
Applying Newton's third law can provide the answer to several questions:
- when an apple falls to the ground, what does the earth do?
- how can rocket propulsion work in outer space, where there is no atmosphere for the
rocket to push itself against? It is a fact that, as recently as a few decades ago, people
(rocket scientists?) claimed that outer space rocket propulsion was impossible since out there
the rocket has nothing to push itself against.
- applicaton of the third law sometimes can be tricky:
suppose I try to move a cart by
pushing on it, the cart is going to push on me with equal and opposite force, and we will not go
anywhere .....
To solve the quandary, it is essential to realize that we must take into consideration
all the forces that are at work. In our case the cart exerts a force on the person; this
force is transmitted from the arms to the feet (by the muscle and bone structure) so that the feet
push backwards on the earth. But then, by Newton's third law, the earth pushes forward on the feet :
if this forward force is larger than the one needed to move the cart, then the cart will move.
When solving problems dealing with Newton's third law you must keep in mind the following rules :
- 1.
- when studying the motion of a body, do take into account all the forces acting on it,
BUT
- 2.
- do not confuse between forces that are applied to the body and forces that the body
applies to others : the two forces that are mentioned in Newton's third law are not
applied to the same body
Normal Force
Look at any object resting on a table : nobody will argue that the object is at rest. Nor
anyone will argue that the object is feeling the force of gravity. But, given that the
object is at rest, there must be another force acting on the body that cancels the
effect of gravity. This force is in fact there, and it is provided by the table itself
(if we were to examine the problem at the atomic level, we would realize that this force
is due to electrostatic repulsion between the electrons in the object and the table).
We conclude that the table produces a force balancing the force that the
object is exerting on it.
And this is exactly what we expect from Newton's third law :
if a body A exerts a force (in this case the weight) on an object B, B will exert an equal and
opposite force on A. This force is usually called the normal force (in mathematical
jargon normal = perpendicular), since it always acts perpendicularly to the surface generating it.
Important example : given an object of weight w, what is the value of the normal force
when the object is resting on a non-horizontal surface?
Equally important is the case when the object and the supporting surface are moving with
some acceleration. You all have experienced the feeling of being heavier or lighter when an
elevator starts or stops. To examine the problem quantitatively, let us suppose that we
ride an elevator while standing on a bathroom scale (the reading on the scale represents the force that
you exert on the scale, therefore, by Newton's 3rd law, the force that the scale exerts on you, i.e.
the normal force). The question is :
what will the reading of the scale be when the elevator is
- 1.
- at rest ?
- 2.
- moving upward with constant acceleration ?
- 3.
- moving downward with constant acceleration less than g ?
- 4.
- moving down with acceleration g? (the cable has broken !!)
- 5.
- moving up or down with constant velocity ?
The correctness of intuitive answers can be verified by Newton's 2nd law : acceleration is
determined by the sum of al the forces acting on you. In this case, the forces are
the weight and the normal force, so that we can write (choosing the positive axis to point up)
FN - mg = ma
FN = mg + ma = w + ma
Assigning to a all the possible values discussed above we get exactly the results we
would expect
Another "hidden" force : Tension
In a large class of problems, we have to deal with objects that are either moved or restrained
by means of a rope, a cable, or the like. For all such cases, it is important to realize that the
rope itself is at the same time subjected to a force and exerting one (as we should expect anyway,
because of Newton's third law).
Example : if you pull a heavy load by means of a rope, you apply a force to the
rope (which also means that the rope is applying an equal and opposite force to you). But the
force you apply to the rope is transmitted to the load; as the rope applies this
force to the load, the load applies the same force onto the rope....
To summarize, there are 4 forces in this problem but (make sure you remark the distinction)
two of them are acting onto the rope, while the other two are applied from the rope to external
objects. The (equal and opposite) forces applied to and from the rope is what we call the
tension.
Examples: what is the rope's tension when
- 1.
- a 50 kg load is hanging from the ceiling
- 2.
- I pull the same load horizonatally, on a frictionless surface, moving with constant
velocity
- 3.
- I pull the same load horizonatally, on a frictionless surface, moving with constant
acceleration a
More examples :
three weights and two pulleys (static case)
Atwood machine (dynamic case)
Friction
The normal force generated by a surface has the property of not being defined a priori, but
to vary according to the force that is applied to the surface (up to a certain limit, after
which the surface collapses). Another type of force that has the same property of not being
defined a priori, but to respond according to the counterforce applied is the
force of friction. Friction plays a fundamental role
in everyday's life. On the one side
you might think that friction is a nuisance: if there was no friction, you could send loads
of arbitrary weight to any far destination while expending hardly any effort : just give
it a small nudge in the right direction, and the load will keep moving in that direction
forever.... But things are not as simple as that, if there was no friction you would not be
able to walk... Or if you wanted to give a nudge to a load to send it somewhere, the
load would send you in the opposite direction with equal force....
Resigning ourselves to the existence of friction, we can study its properties:
- when a body is pulled in a certain direction, friction opposes the force by "pulling" in
the opposite direction : friction (a force, therefore
a vector) acts in the direction opposite to the motion (or attempted motion).
- increasing the pulling force, the frictional force increases accordingly, until one reaches
the "breaking point" . We can then say that friction grows in concert with the force applied,
until it reaches a maximum value. For a given object, this maximum value depends on the
properties of the two surfaces in contact. We quantify this by introducing a coefficient
of friction
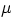 : given two bodies pressing on each other,
the larger is
: given two bodies pressing on each other,
the larger is 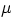 the larger is the force needed to make them slide across each other.
the larger is the force needed to make them slide across each other.
- experience also tells us that, for a given choice of surfaces in contact, friction will increase
proportionally to the strength of the force pressing the bodies together. In other words,
friction is proportional to the normal force.
We can summarize all this by :
From this we see that 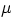 is dimensionless.
is dimensionless.
Important Remark: the expression above is an equality
between vector magnitudes only, and it does not imply equality of direction. In fact
friction and normal forces are orthogonal to each other.
Another lesson from experience is that, in general, it takes a bigger effort to put an object
into motion than to keep it moving. We account for this effect by referring to static (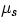 )and kinetic (
)and kinetic (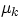 ) friction coefficients.
) friction coefficients.
Example 1 : a 50 kg crate on an inclined plane starts sliding when the angle is 45 degrees. What is
the coefficient of (static) friction ?
Example 2 : when at an angle of 60 degrees, the crate moves with an acceleration g/4. What is the
coefficient of (kinetic) friction ?



Next: About this document ...
Sergio Conetti
9/18/2000