


Next: About this document ...
CHAPTER 6
Dynamics of Circular Motion
From ac = v2/r we can immediately infer that to keep an object of mass m in Uniform Circular Motion, one
needs a (centripetal) force of magnitude
Fc = mv2/r
and directed always towards the center of the circular trajectory. Here are several examples :
- planets and satellites (natural or artificial). Here the force is provided by gravity. Notice that, since
the strength of gravity depends on the distance (i.e. on the radius of the orbit), orbital radius and velocity
cannot be set independently of each other, but, once the radius is chosen, velocity is uniquely determined (and
viceversa). Interesting application: geo-synchronous satellites
- mass rotating on a string. Here the forces at play are gravity and the string tension. The conditions for
uniform motion are:
- 1.
- vertical component of string tension equal to weight of rotating object
- 2.
- horizontal component of string tension with the correct magnitude mv2/r
.
These two conditions effectively create a relation between angle of string and velocity of rotation: the
faster the rotation, the larger is the angle the string makes with the vertical direction. Can the angle ever be
90 degrees ?
- car going around a bend on a flat road : the centripetal force is provided by the friction; the condition to
satisfy is
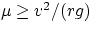
- if the road is banked, there is a specific value of the speed that will allow to go around the bend even in
the complete absence of friction. In this situation, the centripetal force is provided by the component of gravity
directed towards the center of the bend
- the force that keeps a plane in the air is the lift which, as we will learn when studying Fluid
Mechanics,is perpendicualr to the wing's surface. To start curving, it is sufficient for a plane to tilt away from
the horizontal: this will cause the lift to have a horizontal component, which effectively provides a centripetal
force.
- amusement park's bottomless rotating cylinder (problem 6.63). Here the centripetal force is the normal
force of the wall cylinder against you. But, given that in this situation the normal force is purely horizontal,
by itself it could not keep you from falling. But, if there is a normal force, then there is also a friction force,
which is proportional to the normal force and directed against gravity. In conclusion, the more you are pressing
against the walls, the more friction will support you....
- etc.
Non-uniform circular motion
Loop the loop in a roller coaster: this is the case of circular motion with non-uniform speed.
We can verify what common sense tells us, i.e. that the speed of the carriages wil decrease when climbing and increase
when rolling down:
- the forces at play in any instant are gravity and the normal force from the track
- the normal force is always perpendicular to the track's tangent, therefore it is always perpendicualr to the
velocity: being a radial force, it will only affect the direction of velocity, but not its magnitude
- gravity on the contrary, will have in general a radial and a tangential component. The tangential component of the
force will therefore originate a tangential acceleration, which does have the effect of altering the magnitude of the
velocity
What condition has to be satisfied for the carriages (or their passengers) to stay on the circular trajectory?
if the cart is on the track,it means it is somewhat pressing on it, therefore there is a normal force from the
track poiting towards the center. This normal force, together with the radial component of gravity, add up to provide
the centripetal force, i.e., with respect to a reference axis poiting towards the center, and measuring angles away from
the vertical
The limiting point is when the track loses contact with the track, i.e the point at which N becomes 0. This then gives
us a condition for the velocity:
If at any point the velocity is less than the limiting value, then the cart will not go around the loop ( unless it was
solidly connected to the track and the passengers strapped in). In this case you can still go around the loop, but
the force at play, apart from gravity, is not a normal force but a tension: the restraints generate a force directed
away from the center. Let us verify this with formulae. For simplicity, let us look at the highest point in the
trajectory ( ), and suppose that at that point
), and suppose that at that point 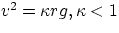 .Let U
(unknown) be the force exerted by the track (I say it is unknown since,at this point,I do not know if it is a normal force
or a tension force)
.Let U
(unknown) be the force exerted by the track (I say it is unknown since,at this point,I do not know if it is a normal force
or a tension force)
mv2/
r =
U +
mg

We then see that U points away from the center: it is not a normal force but a tension, i.e. the bodies going around the
loop do need to be supported.
Sections 6.3 and 6.5 : read and appreciate, but they will not be part of the tests
Resistive Forces
Even though the forces at play when an object is moving against the resistence of a fluid (liquid or gas) are in general
quite complex, two special cases have been recognized:
- 1.
- resistive force proportional to velocity R = kv (typical of slow motion in liquids or of very small objects in
air)
- 2.
- resistive force proportional to square of velocity R = kv2 (e.g. air resistance for large bodies)
When a body is subjected to a constant force (e.g. gravity) and to a force which depends upon
the velocity, it will eventually settle at a constant velocity, referred to as terminal velocity. Terminal
velocity is the velocity at which the magnitude of the resistive force is equal to the magnitude of the constant
force.
Case one : the book discusses the example of an object subjected to gravity and air resistance. We can examine a
different situation, i.e. an object with initial velocity v0 encountering a resistive medium and coming to a halt.
How does its velocity change with time ? In our situation, F = ma becomes
a = dv/dt = -(k/m)v(t)
where the minus sign signifies that acceleration and velocity are in opposite directions. This is a differential
equation, i.e. an equation relating a function with its derivatives. In this case the solution is simple : apart
from the factor k/m, we need to find a function whose derivative is equal to minus the function itself: the answer
will have to involve a negative exponential, since d(e-x)/dx = -e-x. Here is a formal solution:
dv/
dt = -(
k/
m)
v(
t)
dv/
v = -(
k/
m)
dt
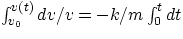
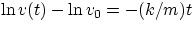

which allows you to compute the value of the instantaneous velocity at any time t. You also see that it takes an infinite
time to reach a complete stop!
Dimensional question : is the argument of the exponent dimensionless, as it should be? the answer depends on the
dimensions of the constant k. We have :
k = Force/velocity = mass x acceleration/velocity =
mass x velocity / (time x velocity) = mass/time
Consequently k/m = 1/time and kt/m is dimensionless.
Case 2 : resistive force proportional to square of velocity. In this case solving the differential equation would
require to find a function whose derivative (apart from multiplicative factors) is equal to the square of the
function itself. We will not try to solve it but, if you are really curious, one solution involves the
hyperbolic tangent (ex-e-x)/(ex+e-x), you can try doing its derivative...
The resistive force is usually expressed as :
with 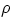 = medium density, A cross section of the object moving through the medium, D empirical, dimensionless
factor. Ine could immediately see that, when falling through air the terminal velocity is
= medium density, A cross section of the object moving through the medium, D empirical, dimensionless
factor. Ine could immediately see that, when falling through air the terminal velocity is



Next: About this document ...
Sergio Conetti
9/22/2000