


Next: About this document ...
CHAPTER 7
Scalar Product of Vectors
Given two arbitrary vectors 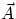 and
and 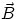 we define their scalar (or dot) product as
where
we define their scalar (or dot) product as
where 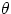 is the angle beteen the two vectors. Note that this can be interpreted either as
is the angle beteen the two vectors. Note that this can be interpreted either as
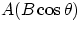 or as
or as 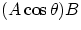 : i.e. either as the magnitude of A times the magnitude of
the projection of B onto A or as the magnitude of B times the magnitude of the projection of A onto
B. From the definition it also follows that
: i.e. either as the magnitude of A times the magnitude of
the projection of B onto A or as the magnitude of B times the magnitude of the projection of A onto
B. From the definition it also follows that
- the result of the scalar product of two vectors is a scalar, i.e. a simple number
(which of course can be positive or negative)
- in fact, the result will be negative when
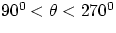
- if
 are parallel
are parallel 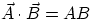 (or (-AB) if anti-parallel)
(or (-AB) if anti-parallel)
- if
 are orthogonal
are orthogonal 
-
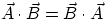
-
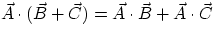
-

From the last result, it also follows that
WORK
In Physics, work takes place when a force acts on a moving object. Specifically, if the force
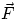 acts on an object during a displacement
acts on an object during a displacement 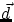 , the work done by the force is
from this, we see immediately that
, the work done by the force is
from this, we see immediately that
- no motion = no work
- force perpendicualr to displacement = no work
- force and displacement at more than 900 = negative work
NB : until now, the sign of physical quantities (velocity, acceleration, force, etc.) was determied by our
choice of the frame of reference. But note that when dealing with work, the choice of sign is not arbitrary
any more, but it is uniquely determined by the relative orientation of force and displacement
In any particular situation, there can be more than one force acting on an object, and we can
estimate the work done by each force. We can also have the case of zero net force : in this case, our object
moves with constant velocity. The net work is zero, even though each of the individual forces
does do some work.
Example : lifting a weight against gravity. How much work do you do? And how much work does gravity do?
and what if, rather than lifting it, I push the same weight up an inclined slope?
Calculating the total work is easy if, during the displacement, the force is constant (both in magnitude
and direction). How can one handle the case of a variable force? Limiting ourselves for simplicity to motion
in the x direction, if a force 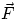 acts during a displacement
acts during a displacement 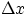 , the work done by the force is
, the work done by the force is
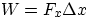
(what about the y component of the force?).
But what if the force is not constant ? You should know the trick : you take small intervals 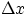 ,during which the force is almost constant, compute the work for all the small
,during which the force is almost constant, compute the work for all the small 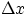 's and sum all the
terms. The smaller you make your
's and sum all the
terms. The smaller you make your 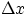 the more accurate the result will be. Therefore, you make them
infinitesimally small, with the result
the more accurate the result will be. Therefore, you make them
infinitesimally small, with the result
Equivalently, you can also say that the total work is given by the area subtended by the Fx vs. x plot.
Important applications :
- 1.
- gravity, F = G m1m2/r2 = k/r2. (if r changes by a large enough amount, we cannot assume
that gravity is constant).
- 2.
- work involving stretched or compressed springs. The starting point is that when a spring is stretched or
compressed by an amount x, it exerts a force F = -kx, k = spring constant, units : N/m. The work
done by a spring when stretched or compressed by a total amount x is then
What is the work done by the compressiong (or stretching) agent?
Question : consider the motion of an object under the sole effect of a spring restoring force. What will its
equation of motion be? (i.e. what will Newton's 2nd law tell us?)
Units for work :
Work = Force x displacement = N x m = joule = J = [ML2T-2]
ENERGY
The concept of energy is constantly present in everyday's life. We are aware that energy comes in many
forms: mechanical, thermal, electrical, chemical, nuclear, etc. A more in depth study would show that
deep down there are only two types of energy :
- 1.
- kinetic, i.e. energy associated with motion
- 2.
- potential, i.e. energy associated with one the fundamental force fields of Nature (gravitational,
electro-magnetic, strong nuclear and weak nuclear).
For the time being, we will just concentrate on mechanical energy, and we will define energy as
the capability of doing work. Obviously this defintion is a bit vague, but it is a fact that, in spite of its
widespread presence and importance, energy is not too easily defined.
Given that a certain amount of energy is related to a certain amount of work, energy will be measured in the
same units as work , i.e. joules (J).
Often used analogy : energy is like wealth, it exists in many forms (cash, stocks, real estate, etc.) and it
continuously transforms from one form to another. In this context, work can be thought of as a financial
transactions : as the transaction transfers wealth from one form to another (or from one person to another),
so work has the effect of transforming energy from one form to another or from one body to another.
Coming back to mechanical energy, let's suppose that a net force 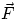 acts on an object of mass m, causing
it to move from
acts on an object of mass m, causing
it to move from 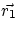 to
to 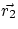 . As usual, it is easier to analyze the situation separately in the x and y
(and z) directions. In the x projection, the total work will be :
. As usual, it is easier to analyze the situation separately in the x and y
(and z) directions. In the x projection, the total work will be :
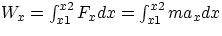 ax
ax =
dvx/
dt = (
dvx/
dx) (
dx/
dt) =
vx dvx/
dx

similarly, one would have found
and, for the total work,
where  = kinetic energy. We then see that
= kinetic energy. We then see that
when a net force acts on a body, the amount of work done by the force is equal to the change in the
body's kinetic energy
Example : spring loaded gun
What if the net force is zero ? The correct guess is that there is no change in kinetic energy (as it should
be : no net force = no acceleration = no change in velocity). But if the net zero force is the consequence
of several forces canceling each other, it is still true that each force does do some amount of work,
therefore there must be some energy transaction involved.
Example :
you push a crate with constant velocity along a surface with friction : you do a certain amount of work, and
friction does an equal and opposite amount. Is there any energy transaction involved ?
Yes : some of your muscular (=chemical) energy is transformed into thermal energy (friction results into
heating of the surfaces).
And what if you lift the crate with constant velocity up to a height h ? What happens to your muscle energy?
find the answer in the next episode
POWER
In the common language, force, energy and power are often used interchangeably, but in Physics
they are clearly distinct entities. We have seen force and energy, let us now introduce power.
If you reach the top of a building either by leisurely walking or by running up the stairs, the total work you
do in either case is the same, but you will not feel the same. The difference is in the amount of time over which
the work was done. We can then define average and instantaneous power
Given that a certain amount of work results in some sort of energy transfer, it is useful to think of power
as the rate at which energy is being transferred.
One also has
Power is measured in watts, 1 W = 1 J/s, or in horsepowers (1 hp = 760 W), while the kilowatt hour is
a unit of energy.
Question : how many horsepowers in one manpower ? to find the answer, time yourself while running up a few flight
of stairs. You will find that, for a short enough period you can work almost as hard as a horse (but a horse
can work like a horse for a full day...)
Section 7.6 : read and enjoy
Section 7.7 : ignore



Next: About this document ...
Sergio Conetti
10/2/2000
![]() acts during a displacement
acts during a displacement ![]() , the work done by the force is
, the work done by the force is
![]() ,during which the force is almost constant, compute the work for all the small
,during which the force is almost constant, compute the work for all the small ![]() 's and sum all the
terms. The smaller you make your
's and sum all the
terms. The smaller you make your ![]() the more accurate the result will be. Therefore, you make them
infinitesimally small, with the result
the more accurate the result will be. Therefore, you make them
infinitesimally small, with the result