


Next: About this document ...
CHAPTER 8
Potential Energy
General Idea : suppose you have a set of objects exerting a force (e.g. gravitational,
electrostatic, nuclear, etc.) on each other. If free to move, the objects would be set into motion by
the force, therefore they would acquire some kinetic energy. We then see that, just by the
fact of being in a region of force ( i.e. in a force field to use the technical term) they
have the capability of doing some work, therefore they have some energy : this type of energy
is what we call potential energy.
Application to Gravity : for a while, we will assume that variations in the force of
gravity can be neglected .
- 1.
- throw an apple up into the air : as the apple climbs, gravity does negative work on it and
"eats away" its kinetic energy (remember :
 ). At its highest point, the apple has lost
all of its kinetic energy, but is this energy lost? No, since at its highest point the apple has the
potential of regaining all of its initial kinetic energy by falling back to the ground
(and it doesn't matter if it does so immediately or keeps it for later, as would happen if the apple
was thrown onto a high shelf); we then say that at the top of its trajectory the apple has some
potential energy. How much ? As much as the amount of work that could be done when it falls
back to the ground, i.e. W = F d = mgh, where h is the height reached.
). At its highest point, the apple has lost
all of its kinetic energy, but is this energy lost? No, since at its highest point the apple has the
potential of regaining all of its initial kinetic energy by falling back to the ground
(and it doesn't matter if it does so immediately or keeps it for later, as would happen if the apple
was thrown onto a high shelf); we then say that at the top of its trajectory the apple has some
potential energy. How much ? As much as the amount of work that could be done when it falls
back to the ground, i.e. W = F d = mgh, where h is the height reached.
- 2.
- a similar result would be obtained if I was to lift the apple with constant velocity up to
h : to do this I have to do the work mgh (and the gravity does the work -mgh ). When the
apple reaches the height h, it has acquired the potential energy mgh
A more precise statement would be that, in both cases, the (potential) energy of the apple/earth system
has increased. How was such an increase made possible? In the first case at the expense of the apple's
initial kinetic energy, in the second case at the expense of my own stored muscular energy. In both
cases we have witnessed an energy transfer, which was mediated by some work being done.
We then conclude that an object of mass m at a certain height h has a potential energy
U = mgh
When an object goes from a height h1 to a height h2 its change in potential energy is
 (note :
(note : 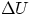 can be positive or negative) and this change is
equal and opposite to the work done by gravity during the change
This result tells us that the change in potential energy (or, which is the same, the work done by
gravity) depends only on the final and initial positions, independently of the path followed.
Let's verify it in a simple, but fairly general case :
can be positive or negative) and this change is
equal and opposite to the work done by gravity during the change
This result tells us that the change in potential energy (or, which is the same, the work done by
gravity) depends only on the final and initial positions, independently of the path followed.
Let's verify it in a simple, but fairly general case :
your apple is at a height h and you let it reach the ground
- 1.
- just by dropping it
- 2.
- throwing it up vertically and then letting it drop
- 3.
- throwing it at an angle, so that the apple will follow a parabolic trajectory
What is the work done by gravity in each case?
A force whose total work done on an object depends only on the initial and final position and not on
the path followed is called a conservative force (the name comes from the fact that when
such forces are at play mechanical energy is conserved).
Whenever a conservative force is present, potential energy is present, with the general definition:
and
i.e. the difference in potential energy between two points is given by minus the work done by the force
responsible for the potential,when going from one point to the other. From the above definitions it also
follows that
This relation between force and potential function has some interesting consequences.
Examining for simplicity a one-dimensional case, the expression
F = -dU/dx
tells us that when the potential function has an extreme value (a minimum or a maximum) then the
corresponding force is zero. And,if the force is zero,in the absence of other forces an object initially
at rest will remain at rest : potential maxima and minima correspond to situations of equilibrium.
Moreover one could see (see section 8.7) that maxima correspond to unstable equilibrium while
the equilibrium is stable for the minima.
Visualizing the potential curve (and the meaning of its maxima and minima) is quite easy for the case of
gravitational energy, but expressing forces in terms of their potential function is an extremely useful
tool in a large class of physical phenomena.
Going back to gravity, we can see a quandary. Suppose you climb the ladder leading
to a diving platform : you would be inclined to say that your potential energy is mgh, where h is the
height of the ladder, but shouldn't you really compute your energy with respect to the bottom of the
pool?
To solve the quandary we should notice
that the potential energy function is defined as an indefinite integral, suggesting that the value of
potential energy is defined only up to an arbitrary additive term. This is consistent with the fact that,
in any physical process, what comes into play is always the difference in potential energy
between two points, therefore we can assign zero potential energy to any arbitrary convenient location.
In our example, if we assign 0 potential energy to the bottom of the ladder, then the bottom of the pool
has a negative value of potential energy, but that's OK : the only thing that matters is the change in
energy if I dive onto the floor or into the water reaching the pool's bottom, and these differences do
not depend upon my choice of 0-level reference.
Another Potential Energy: Elastic Energy. A compressed spring clearly has potential energy,
since it can do work when released. Moreover, the work done by the spring depends only on its initial
and final position. We have seen in fact that to compress a spring by an amount x the work done is
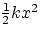 (and the spring itself does an equal and opposite amount of work). We then conclude
that the spring's force is conservative, and the potential energy associated with a spring which is
compressed (or stretched) by an amount x is
(and the spring itself does an equal and opposite amount of work). We then conclude
that the spring's force is conservative, and the potential energy associated with a spring which is
compressed (or stretched) by an amount x is 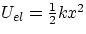 .
.
Conservation of Mechanical Energy
We have seen that when a net force does net work on an object
(this is true for any net force, be it conservtive or not). But for conservative forces we also have:
therefore , if only conservative forces are present
any gain(loss) in kinetic energy is compensated by an equal loss (gain) in potential energy.
And also:
K2-K1 = -(U2-U1)
K2+U2 = K1+U1
the sum of kinetic + potential energy is constant
This result is an extremely powerful tool to reach an easy solution for a large class of problems.
Examples:
- pendulum
- gun shooting straight up or straight down. How will the bullet velocity compare at the bottom ?
- loop the loop : from what height should I start, to make it around the loop ?
- bungee jumping
- etc.
And what if some non-conservative forces are involved ? We can guess the answer : the mechanical
energy of the system is non-conserved. And the change of energy (either gain or loss) in the system
will be equal to the net work done by the non-conservative forces. Specifically:
More examples :
- lifting a crate of apples from the ground to a shelf
- a car engine providing a constant force (ignore friction and air resistance)
- 1.
- on a flat road
- 2.
- up a slope
- firemen sliding down a pole
- etc.
Sections 8.9, 8.10 : skip



Next: About this document ...
Sergio Conetti
10/6/2000