


Next: About this document ...
Chapter 9
Impulse, Momentum and Collisions
We are going to take another look at Newton's second law, the way that Newton himself actually
looked at it. So far, we have written  , but remembering that
, but remembering that 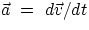 , we can write
where
, we can write
where 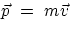 is the momentum. This expression is more general than the
standard F = ma, since it allows for the mass to change (e.g. leaky containers, rockets burning fuel,
sub-atomic particles, where mass can change into energy and viceversa, etc).
is the momentum. This expression is more general than the
standard F = ma, since it allows for the mass to change (e.g. leaky containers, rockets burning fuel,
sub-atomic particles, where mass can change into energy and viceversa, etc).
By integration, one gets:
which is also equivalent to
where 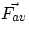 is the average force acting during the interval
is the average force acting during the interval  .
This expression is extremely useful, since it allows to study phenomena that occur
over very short times by relating quantities that would be difficult to measure (e.g. the force present
between a baseball and the bat) to more easily measurable quantities (i.e. the velocity of the ball
before and after the hit).
.
This expression is extremely useful, since it allows to study phenomena that occur
over very short times by relating quantities that would be difficult to measure (e.g. the force present
between a baseball and the bat) to more easily measurable quantities (i.e. the velocity of the ball
before and after the hit).
Example : what is the use of air bags?
In a car crash, the car, and its occupants, rapidly change their
momenta from mv to 0. To minimize the effect of the impact, we want to decrease the average
force acting on the car occupants. For a given 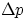 , we can make Fav as small as possible by
making
, we can make Fav as small as possible by
making  (i.e. the time over which the change of momentum occurs) as large as possible.
(i.e. the time over which the change of momentum occurs) as large as possible.
Conservation of (Linear) Momentum
From
we see that if no net force is acting on a "system", its total momentum remains constant.
So far we have mostly studied the motion of individual objects but this result allows us to
investigate more complex situations, where several objects interacting with each other are
involved. If we have a "system" comprising several bodies, we should distinguish between
internal and external forces :
- 1.
- we call internal, the forces acting between members of the system, while
- 2.
- we call external the forces due to some agent which is not part of the system
Considering the case of a system where no external forces are present (i.e. the only forces
present are internal, this is also called an isolated system), Newton's third law requires that the
totality of all internal forces adds up to zero. : for every force that a given member of the system A exerts on
a member B, B will respond with an equal and opposite force, and this is true for every (internal) force
present. We can than conclude that, for an isolated system, all the forces add up to zero,
therefore 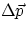 = 0, i.e.
= 0, i.e.

constant
where the sum runs over all the individual momenta of the members of the system. This expression representing
a vector sum implies that the sum of the components must be separately equal to some constant
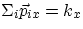
and

, with
kx,
ky= constants
Examples :
- 1.
- measure the velocity of a speeding bullet
- 2.
- a bomb (at rest) explodes into three pieces
- 3.
- a moving projectile breaks up into two pieces
Remark : when deciding whether momentum is conserved or not, make sure you are clear on what
is your "system", and what are the external and internal forces. Example : when an apple falls to the ground,
its momentum is not conserved. In which system would we have momentum conservation?
Momentum conservation is routinely exploited to analyze collisions. For these cases, in addition
to momentum conservation we can, under certain circumstances, also apply Kinetic Energy
Conservation. When dealing with collisions, we distinguish 3 cases:
- 1.
- Elastic Collision : we define an elastic collision one in which both momentum and kinetic
energy are conserved. The colliding objects bounce off each other elastically.
- 2.
- Inelastic Collisions : in this case, typical e.g. of car crashes, momentum is conserved,
but total kinetic energy is not, since part of the input energy causes permanent deformations
plus heating by friction.
- 3.
- Totally Inelastic Collision : this is the extreme case, where the colliding objects
stick together after collision (it could be shown that this case represents the maximum possible
energy loss compatible with momentum conservation).
We can investigate under which circumstances full knowledge of the individual masses and velocities before the
collision allows us to determine the corresponding variables after the collision. Let's examine separately the
one-dimensional and two-dimensional cases:
- one dimensional collisions : if we know masses and velocities before the collisions, the two unknowns are
the velocities after collision. Are they uniquely determined ?
- 1.
- elastic collisions : in this case we can require both momentum and kinetic energy conservation. With two
unknowns and two equations, the solution is unique
- 2.
- totally inelastic collisions : in this case there is only one equation, corresponding to momentum
conservation, but we only have one unknown (the two colliding objects stick together, therefore there is only one
unknown velocity). Again there is a unique solution, and once the problem is solved, you can also compute how much
mechanical energy was lost
- 3.
- inelastic collisions : having only one equation and two unknowns,the problem is not defined. Full knowledge of
the pre-collision quantities is not enough, we need some extra information (e.g. how much energy was lost in the
collision)
- two dimensional collisions : here in general there are 4 unknowns, i.e. the x and y components of the
velocities of both colliding objects, and the equations we can write are at most 3, i.e. momentum conservation
for both the x and y direction and, when applicable, energy conservation. In general extra knowledge is needed
to fully solve the problem. Example : glancing (elastic) collision between billiard balls, one of them being
initially at rest. After collision, the
the balls can scatter at any angle, but if we know the angle of one of the two we can uniquely determine the
other (one could also see that, in elastic collision among equal mass objects the two angles always add up to 900).
Center of Mass
Given a system of many particles, if  is the position of the ith particle with respect to an arbitrary
origin, we define their center of mass the point of location
As usual, for most situations an analytical determination of the center of mass will be done through the vector
components, viz.
is the position of the ith particle with respect to an arbitrary
origin, we define their center of mass the point of location
As usual, for most situations an analytical determination of the center of mass will be done through the vector
components, viz.
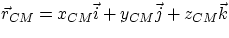
, with
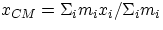
and similar expression for the other coordinates. Whe dealing with a solid object rather than a collection of discrete
masses, the definition can be extended as
Some tricks to simplify the calculations ;
- if the objects (or collection of objects) is symmetric about a point, a line or a plane, the center of mass will
be located on that point/line/plane
- a complex object can sometimes be thought of as the combination of several parts (e.g. "Mickey Mouse"). It is then
convenient to find the c.o.m. of each part, and then find the c.o.m. of c.o.m.'s
- choose your axes wisely : if the system is a group of particles, set one particle at the origin. If it has a line
of symmetry, choose that line as one of your axes
The center of mass is particularly important in mechanics, since one could see that
The center of mass of a body or a system of bodies moves as though all of the mass were concentrated there,
and all external forces were applied there
In formulae, this corresponds to ( see the book for a proof)
which applies both to a solid body or to a collection of separate bodies. One could also see that the total momentum of
a collection of masses is related to the center of mass velocity by
For example, if a projectile, following a parabolic trajectory under the influx of gravity, explodes in mid air, its
fragments will move in such a way that their combined center of mass keeps following the same parabolic trajectory.
Moreover, for an isolated system (i.e. no external forces) if the center of mass is
initially at rest (or moving with constant velocity).it will continue doing so, regardless of the (internal) forces and
interactions that occur among the components of the system:
if a bomb explodes while at rest, the motion of its fragments will be such that their combined center of mass
remains at rest. Similarly, if you stand on a board resting on a frictionless surface, as you start moving in one
direction the board will move in the opposite direction,so as to keep the position of the center of mass constant.
Section 9.8 : skip



Next: About this document ...
Sergio Conetti
10/10/2000
![]() , we can make Fav as small as possible by
making
, we can make Fav as small as possible by
making ![]() (i.e. the time over which the change of momentum occurs) as large as possible.
(i.e. the time over which the change of momentum occurs) as large as possible.