


Next: Problem 12.9
Up: No Title
Previous: No Title
12.6. a)
We know that the solution must take the form of
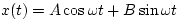
where And B are constants that we have to determine.
If we substitute in the value t=0, we find
x(0) = x0 = A
so, immediately we know that constant. Now, let's take a derivative
of our equation.
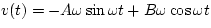
Again, if we substitute the time t=0, we find
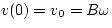
or that

substituting again, we get that our equations for x(t) and v(t)
reduce to what we were looking for
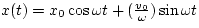
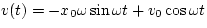
b)
Now, we are trying to show the identity
v2-ax = 0
We have x(t) and v(t) from part a), now, to find a(t), we
differentiate.

substituting into the equation, and using the identity that

we find that
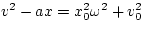
Well, since this has no time dependence, we can evaluate this at any
time and the answer is independent of that time. Therefore,
v2 - ax = v02 - a02 x02
Now, let's evaluate this at a maximum in position. In other words,
at a turning point of the osciallator, then we find
v = 0, x = A
Then the equation reduces to
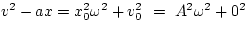
or 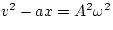



Next: Problem 12.9
Up: No Title
Previous: No Title
Jason George Zeibel
12/4/1997