


Next: About this document ...
Quiz #4
Name:
SSN:
This quiz is due at the beginning of class on the 5th of December
(Friday). You are on your honor not to consult others or reference
materials in the completion of this quiz. This includes textbooks and
notes.
Please review chapter 12 material before beginning this quiz. If you
can't figure out an answer to one part, make a guess, and use that answer
in
the following parts.
Sign pledge here:
1.) (25 Points) A 1.5 kg object that stretches a
particular spring 2.8 cm from its natural length when hanging at rest
oscillate with an amplitude of 2.2 cm.
General Comments:
I accepted a lot of answers on this quiz becuase the wording of the
question aparently confused the majority of the class. Below is the
intended solution. Please come see me if you are still unsure of why
this is the correct solution.
a) What is the total energy of the system?
Solution:
The answer to this depends on the fact that gravitational potential
energy of the system is zero at the equillibrium of the oscillations.
In other words, when the spring is hanging motionless at the end of
the spring (at equillibrium), the gravitational potential energy of
the system is zero. At that point, there is potential energy in the
spring because it is stretched a distance of .028 m.
First, we need to find the spring constant, k. When hanging at
equillibrium, the sum of the forces is equal, so
mg = kx
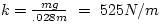
Now, consider the object while its oscillating. At the lowest point
of its oscillation, the total energy of the system is a sum of the
potential energy stored in the spring and the gravitational potential
energy. At this point, the kinetic energy is zero.
Etot = Uspring + Ugravity
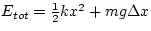
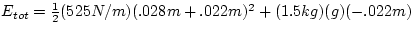
Note that the x used in the spring force is the TOTAL stretch of
the spring and is measured from the point
when the spring was unstretched, or x = 2.8 cm + 2.2 cm.
Etot = .656 J - .324 J
Etot = .333 J
b) If the gravitational potential energy of the system is defined to
be zero when the object is in equillibrium, then at maximum downward
displacement find the gravitational potential energy.
Solution:
If the zero of the potential energy is zero at equillibrium, then if
the object is oscillating with an amplitude of 2.2 cm about
equillibrium, then
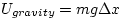
Ugravity = mg(-.022 m)
Ugravity = -.324 J
c) Also at maximum downward displacement, find the potential energy
stored in the spring.
Solution:
This one fooled almost everyone. The total amount that the spring is
stretched is 2.8 cm + 2.2 cm = 5.0 cm, so the potential energy in
the spring is

Uspring = .656 J
d) Find the kinetic energy of the object when displaced halfway from
equillibrium, or 1.1 cm.
Solution:
I didn't state whether this was above or below the equillibrium
position, so either answer was acceptable. Below is the case for the
object 1.1 cm BELOW equillibrium.
The easiest way to do this is with conservation of energy.
Etot = KE + Uspring + Ugravity
so the kinetic energy at x = 1.1 cm is
KE = Etot - Uspring - Ugravity
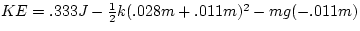
KE = .333 J - .399 J - (-.162 J)
KE = .096 J
e) Write an equation for the position and for the velocity of the
object as a function of time t, and the values given in the problem.
Choose t=0 when the object is at the equillibrium position. Recall
that
Solution:
The general form of harmonic motion as a function of time is

Where we know that 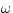 is given by
is given by
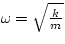
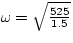
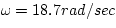
We also realize that the constant A is the amplitude of oscillation,
here
A = .022 m
The problem left is finding the constant 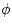 . Plugging in when
t=0, we find,
. Plugging in when
t=0, we find,
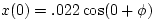
and at t=0, we were told that the object was at the equillibrium
position, or
x(0) = 0
So, 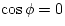
which implies that

So, the solution for the position of our of object as a function of
time is
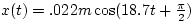
Now, to find the velocity as a function of time, we take the
derivative of the position.
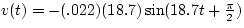
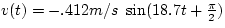



Next: About this document ...
Jason George Zeibel
12/10/1997