


Next: Problem 20.3
Up: No Title
Previous: Problem 19.36
19.43. a)
Again, to determine the electric field, we turn to Gauss' Law.

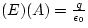
The Area of our Gaussian surface is given by
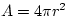
For r<a, the charge q varies as a function of the radius. The
enclosed charge is given by
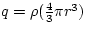
So, the electric field is given by
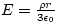
For a<r<b, and r>c, the electric field is just that of a point
charge centered at the origin, or

or, more familiarly written,
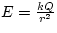
Inside the conductor, the net enclosed charge is zero, and therefore
the electric field is zero.
b)
The definition of surface charge density is charge per unit area.
So, for the inner surface, a total charge of -Q is present to
balance that of the point charge at the origin, so the surface charge
density is given by
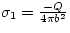
and on the outer surface, a total charge Q is present to balance
the -Q on the inner surface since the total charge is zero on the
conductor. Therefore, the surface charge density on the outer
surface is given by
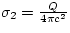
Jason George Zeibel
1/29/1998