Problem 21.3

21.3.
We know that current is charge per unit time, so since we are given
$I(t) = I_{0} e^{-t/\tau}$
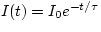
then combining that with
$I(t) = \frac{dQ(t)}{dt}$
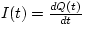
we find that the charge passing a certain point in a time dt is given by
dQ(t) = I(t) dt
So, the charge passing a point in a time t is given by
$Q(t) = \int_{0}^{t}I(t') dt'$
$Q(t) = \int_{0}^{t}I_{0} e^{-t'/\tau} dt'$
$Q(t) = I_{0} \tau (1 - e^{-t/\tau})$
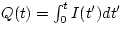
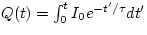
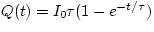
So, if we substitute in the value 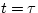$t = \tau$, we find
$Q(t) = I_{0} \tau (1 - e^{-1})$
$Q(t) = (.632) I_{0} \tau$

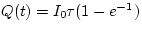
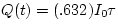
b) If we substitute in the value 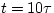$t = 10\tau$, we find
$Q(t) = I_{0} \tau (1 - e^{-10})$
$Q(t) = (.99995) I_{0} \tau$

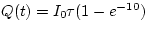
c) If we substitute in the value 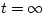$t = \infty$, we find
$Q(t) = I_{0} \tau (1 - e^{-\infty})$
$Q(t) = I_{0} \tau$
which shouldn't surprise us. This is just saying that all the initial charge passes by the point we are looking at eventually.