Problem 2

 

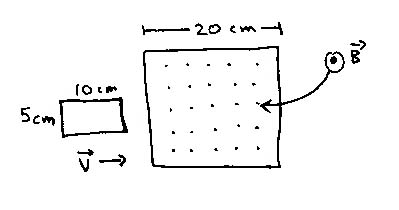
2.) (15 points) A 10 cm by 5 cm loop of wire with resistance of $2.5 \Omega$ is pulled through a region of uniform magnetic field B = 1.7 T out of the page, with a constant speed $\hat{v} = 1.0 cm/s$. The B field is normal to the loop. The front end of the loop enters the region of magnetic field at time t = 0. The region of B field is 20 cm wide. Neglect any effects of self inductance and therefore don't worry about the fact that your graph has sharp ``edges''.
 
a)   Find and graph the magnetic flux as a function of time for 0<t<30.
 
b)   Find and graph the induced emf as a function of time for 0<t<30.
 
c)   Find and graph the current in the loop as a function of time for 0<t<30.

Answer:
a)
Since the area that is in the field is changing, the flux is changing as well. Note that initially and at t>30, the flus is zero. Also that for time 10<t<20, the entire loop is in the B field and therefore the flux is constant. The equations determinig the flux are given by
$\Phi = \vec{B} \cdot \vec{A}$
$\Phi = BA(t)$
For 0<t<10, we have
$\Phi = (.1)(.05)(.1 m/s)(1.7 T)t$
$\Phi = .00085 t$
For 10<t<20, we have
$\Phi = .0085$
and for 20<t<30, we have
$\Phi = .0085 - .00085 t$
That gives us this graph.

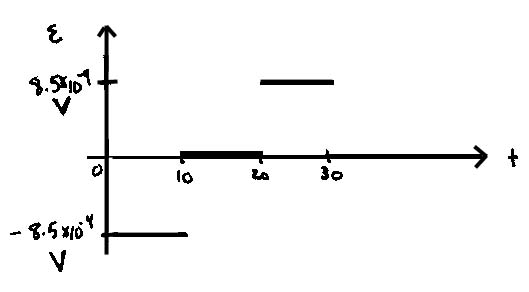
b)
To find the emf, we simply make use of the equation,
$\epsilon = -\frac{d\Phi}{dt}$
So, our graph of the emf whould be the derivative of the graph of the flux. Equation wise we have zero emf when the flux isn't changing and therefore, for the time 10<t<20, we know that $\epsilon = 0$
For 0<t<10, we have
$\epsilon = -8.5 \times 10^{-4} V$
and for 20<t<30, we have
$\epsilon = 8.5 \times 10^{-4} V$
The graph looks like

c)
We simply use Ohm's law to find the current in the circuit. That gives us
$I = \frac{\epsilon}{R}$