Problem 1

1.) (15 points) A rocket with a length of 1000 m as measured in the frame of the rocket, is moving in the $\hat{x}$ direction with a speed of .6 c with respect to an observer on the ground. An astronaut stands at the rear of the rocket and fires a bullet toward the front of the rocket at .8 c relative to the rocket. How long does it take the bullet to reach the front of the rocket ...
(a) as measured in the frame of the rocket?
(b) as measured in the frame of the bullet?
(c) as measured in the frame of the observer on the ground?

 
Answer:
a) In the frame of the rocket, the rocket is 1000 m long and the bullet is travelling at .8c. Therefore, the time to get to the end of the rocket is given by:
$t = \frac{d}{v}$
$t = \frac{1000 m}{.8 c}$
$t = 4.17 \times 10^{-6}$ seconds
$t = 4.17 \mu s$
 
b) In the frame of the bullet, the rocket is travelling by at a speed of .8c. Therefore, the rocket is shorter than 1000 m to the bullet. To find out how much we use length contraction.
$L' = \gamma L$
$\gamma = \frac{1}{\sqrt{1 - \frac{(.8c)^{2}}{c^{2}}}}$
$\gamma = 1.67$
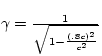
So, we are looking for the length L.
$L = \frac{L'}{\gamma}$
$L = \frac{1000 m}{1.67}$
L = 600 m
So, the rocket ship is only 600 m long in the frame of the bullet. Therefore, since the rocket ship is travelling past the bullet at .8c, it takes
$t = \frac{d}{v}$
$t = \frac{600 m}{.8 c}$
$t = 2.50 \times 10^{-6}$ seconds
$t = 2.50 \mu s$
for the bullet to get to the end of the rocket ship.
 
c) Part c) caused confusion for a lot of people. There are (at least) two different ways to do this part. I will go through them both. Good job for those that figured out other ways. The beauty of special relativity is that there are lots of different ways to look at the same problem.
First of all, the way that I did it...
The full Lorentz time transformation equation says:
$t' = \gamma (t + \frac{v x'}{c^{2}})$
The second term vanishes if the two events that we are concerned with happen in the same location in the primed system. If that happens, then the time between events is called the proper time. In the frame of the earth and the frame of the rocket, the two events, namely the event of the bullet being fired and the event of the bullet hitting the end of the rocket happen in different places. Therefore, neither of these frames can have the proper time and the previous equation does NOT reduce to
$t' = \gamma t_{p}$
Only in the proper time frame will this work. So, let's consider the frame of the rocket. Here, the first event and the second event (the firing of the bullet and the bullet hitting the end of the rocket) are separated by a distance of 1000 m. (the length of the rocket in its own frame) So,
x' = 1000 m
And since the rocket is moving with a velocity v = .6c with respect to the observer's frame, we know that
v = .6 c
$\gamma = \frac{1}{\sqrt{1 - \frac{(.6c)^{2}}{c^{2}}}}$
$\gamma = 1.25$
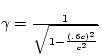
So, plugging in, we find that
$t' = (1.25) (4.17 \mu s ~+~ \frac{(.6 c)(1000 m)}{c^{2}})$
$t' = 7.71 \mu s$
 
The other approach is to acutally figure out in what frame the proper time exists. This isn't hard. To the bullet, the event of it leaving the gun and the event of it hitting the end of the rocket happen in the same location. This is so since the bullet is at rest in its own frame. So, the trick is to find the velocity of the bullet in the earth's frame. The time interval in the bullet's frame is the proper time, so we have
$t' = \gamma t_{p}$
$t' = \gamma (2.50 \mu s)$
To find the velocity of the bullet in the earth's frame, we use the velocity addition formula.
$v = \frac{u + v'}{1 + \frac{u v'}{c^{2}}}$
Where I have used v' to be the velocity of the bullet in the rocket's frame and u to be the velocity of the rocket.
$v = \frac{.6c + .8c}{1 + \frac{(.8c)(.6c)}{c^{2}}}$
v = .946c
So, we have a $\gamma$ of
$\gamma = \frac{1}{\sqrt{1 - \frac{(.946c)^{2}}{c^{2}}}}$
$\gamma = 3.08$
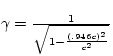
So, putting this into the time dilation equation, we have
$t' = \gamma t_{p}$
$t' = (3.08) (2.50 \mu s)$
$t' = 7.71 \mu s$