MAPPING TRANSISTOR CHARACTERISTICS

1. Identify the emitter lead and plug it into the top row of one of the columns in the lower half of the board as shown in Fig. 9.

Figure 9:Layout of Transistor and leads on breadboard

Plug the two remaining leads - without crossing them - into the bottom row of two different columns in the top half of the board. Seen from the top the base will now be on the right and the collector on the left. Use the variable power supply on the top left of the designer board to supply the collector voltage, and the one on the right to supply the base voltage (that way you don't need to cross the wires).

2). Using the circuit shown below (which when layed out actually looks like this ) , map the characteristics of the transistor by injecting a known current into the base of the transistor.

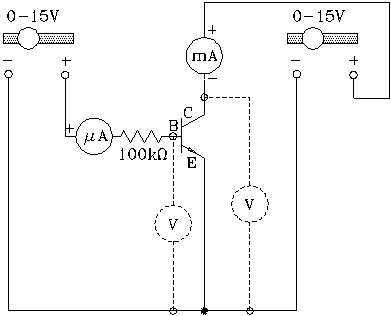
Figure 9:Circuit for Transistor Characteristics

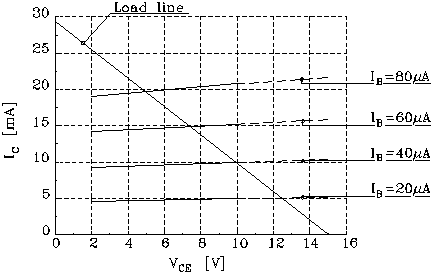
For this first experiment replace the 47 (yellow, purple, black) and the 470 Ohm (yellow, purple, brown) resistors shown in Fig. 9 with short wire bridges. Use the base power supply to set I_B to 20 mA. Readjust the slide as necessary to keep I_B at that value as you vary V_CE with the upper left power supply in steps of 2 volts, while reading I_C. Below 2 V the collector current varies very rapidly with the collector voltage. Don't measure in this region, it is outside the normal operating range of the transistor and of no interest. Repeat your measurements for I_B = 40, 60, and 80 mA. Do not let the collector current exceed 25 mA or you might damage the transistor. Plot your results to get a set of curves similar to the ones shown in Fig. 10.

Figure 10: Transistor characteristics curve

Look at your graph. After the steep rise (omitted in your plot) the collector current levels off. The value of I_C in the flat parts is different for each I_B. In fact, if V_CE is held fixed, say at 6 V, I_C is nearly proportional to I_B. Check this by calculating the ratio I_C/I_B at V_CE = 6 V for each value of I_B. This ratio, usually given the symbol b, is an important parameter called the base to emitter current gain of the transistor.

b = I_C/I_B ------------Eqn.(3)

(Taking into account that you measured I_C in milliamps and I_B in microamps, b should be between 50 and 200.) Extract from your plot values of b at various values of V_CE and I_C. Does b change much as a function of either variable? The circuit that you have built is a (nearly) linear current amplifier: I_C is controlled by I_B, is much larger than it and, over a considerable range, is nearly proportional to I_B.

3). Change the leads of the voltmeter to read V_BE. Set the collector voltage V_C to 10 V and use the right slide resistor to vary V_BE, (without exceeding I_C= 25 mA) . Note that, even though both base and collector current vary greatly, V_BE remains nearly constant at about 0.6 V. No matter how much current is drawn, the base remains at nearly the same potential as the emitter.

Calculate the gain of a voltage amplifier as shown in Fig. 11, using R_E = 47 W, and R_C = 470W. This calculation requires some thought because a changing output voltage across R_C results in a changing collector voltage V_C. In Fig. 11 the voltages are defined with respect to the negative terminal of the power supply which we will call common or ground.

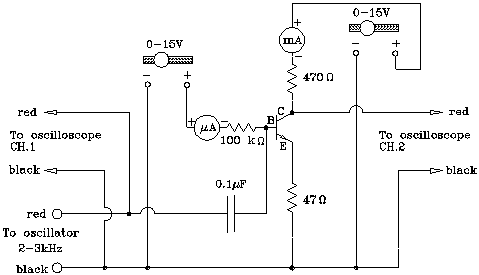
Figure 11:Voltage Amplifier

If we want to refer to a voltage difference between two arbitrary points we use a double subscript, i.e. V_CE = V_C V_E. The currents are defined as before. First note some obvious approximations that you can make: From I_B << I_C follows:

I_E ~ I_C = bI_B ---------------------Eqn.(4)

From V_BE<< V_CE follows;

V_B ~ V_E. -------------------Eqn.(5)

Referring to Fig. 11, you see that

V_E = R_E I_E ~ R_E bI_B ~ V_B. ----------------------Eqn.(6)

From this you can calculate the input resistance R_in of the amplifier. This is an important quantity since it tells us how much current the input will draw if we apply a voltage to it.

R_in = V_B/I_B ~ V_E/I_B ~ bR_E. ------------------Eqn.(7)

A good voltage amplifier should have a large input resistance, otherwise it would load down the voltage that one wishes to amplify. It is comforting to see that in our amplifier the current amplification b, which is of the order of 100, appears as a multiplicative factor in the expression for this resistance. You can also calculate I_C:

I_C = bI_B ~ V_B/R_E. ----------------------Eqn.(8)

The collector voltage V_C is obviously given by

V_C = V - I_C R_C. -------------------Eqn.(9)

But, what you really want to know is not the collector voltage but the output voltage, which we define as the change of the collector voltage that results from a given change of the input voltage. In other words we would like to know DV_C as a function of DV_B. Since V and R_C are constants, we can write

DV_C = - R_C DI_c = - DV_B (R_C/R_E), --------------------Eqn.(10)

where the minus sign indicates that a positive DI_C gives a negative DV_C. We can now calculate what is called the small signal voltage gain g of the amplifier

g = DV_C/DV_B = - R_C/R_E ----------------------Eqn.(11)

Note that in this approximation, which holds only for the case b >> 1, the gain g is independent of the current gain b and is given simply by the ratio of two resistors. This is a very desirable feature:

!The current gain varies from one transistor to the next whereas it is easy to make resistors that have a well defined value.

!The current gain of a transistor varies with the collector current I_C, resistors remain constant.

!The current gain of a transistor varies with temperature. Resistors can be made to be temperature independent.

We have said above that in many applications the change of a signal is more important than its absolute value. This is especially true for signals that have a time average of zero. Such signals are called a.c. signals, (for a.c. = alternating current). The signals in an audio amplifier are a typical example.