1. A laser is emitting light towards you at frequency f in the laser frame of reference. You are traveling directly towards the laser at relative speed v.

 (a) What is the frequency f' of the laser light as observed by you? (If you know the answer, just write it down -- no need to derive it.)

 (b) Write down the Lorentz transformations for energy and momentum of a particle between two frames having relative velocity v along the x-axis.

 (c) From (b), find how the energy of a photon changes between the frames.

 (d) From (a), (c) show that Einstein's quantization of electromagnetic radiation was

Lorentz invariant.

 2. Antiprotons were first created by the reaction: 

Assume the energy is just sufficient for this reaction to occur.

(a) In the center of mass frame, what is the relativistic mass of one of the incoming protons?

 (b) What is the speed of an incoming proton in the center of mass frame?

 (c) State the addition of velocities formula.

 (d) In the lab frame, one of the initial protons is at rest. Use (c) to find the incoming speed of the other proton.

 (e) From (d), what is the kinetic energy of the incoming proton? (You can give it in terms of the proton rest mass energy, with a bonus point if you can give it also in electron-volts.)

 3. (a) Explain briefly why Rutherford concluded from his a -scattering experiment that atoms have nuclei. What were the essential properties of the nucleus needed to explain his results?

 (b) He used a -particles from polonium, the a 's had a speed of 1.6 x 10⁷ meters per second (but ignore relativistic corrections in this question). Assuming the scattering pattern agreed with that predicted by using the Coulomb force, what can you conclude about the size of the gold nucleus (charge = 79)? (Hint: find how close one of these a 's could get to that nucleus.)

 (c) Would you expect the experiment to work if b rays had been used instead of a 's? Explain why or why not.

 (d) Would you expect the experiment to work if g rays had been used instead of a 's? Explain why or why not.

4. A one-dimensional simple harmonic oscillator consists of a mass m connected to the origin by a spring of spring constant k, so the classical equation of motion is:

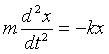
(a) Write down the potential energy corresponding to displacement x.

 (b) Write down the kinetic energy in terms of momentum p (assumed nonrelativistic).

 (c) Write down the total energy of the system.

 (d) State and briefly explain Heisenberg's uncertainty principle.

 (e) Use (d) to estimate the minimum possible energy in the simple harmonic oscillator, in terms of k, m and h.

 (f) State how your answer to (e) relates to the frequency of the oscillator. Is your result exact? Should it be?

 5. (a) Write down the time dependent full Schrödinger equation for a particle of mass m moving in one dimension in a potential V(x).

(b) Derive the time-independent equation by separation of variables.

(c) Solve the equation to find the two lowest lying states in a square well of size L, and infinitely high walls, call the wave functions y ₁(x,t) and y ₂(x,t).

 (d) Estimate the size L of this well if the particle is an electron, and a yellow photon can excite it from the lowest state to the next.

 (e) Is the function y ₁(x,t) + y ₂(x,t) a solution to Schrödinger's equation? In what way is the time dependence of this state different from those above? Give a physical interpretation of the difference.

6. (Give a one or two sentence statement of the most important relevant facts.)

(a) Why do metals reflect light so well?

 (b) Why are some electroscopes discharged by exposure to ultraviolet light but not by visible light?

 (c) Why do x-rays penetrate flesh better than bone? (Explain what mechanism in bone absorbs the x-rays.)

 (d) Why are heavy nuclei less stable than light nuclei?

 (e) Over what range, very approximately, does the half-life for a -decay vary? Over what range (again very approximately) does the energy of the emitted a 's vary? What -- if any -- is the connection between these ranges?

 (f) State briefly how Einstein explained the decrease in specific heat of a solid at very low temperatures.

 (g) Unlike more familiar objects, electrons are indistinguishable from each other. What constraints does that place on a wave function y (x₁, x₂) describing two of them? How is that related to Pauli's exclusion principle?