Particles in Two-Dimensional Boxes

Michael Fowler, University of Virginia

Separation of Variables in One Dimension

We learned from solving Schrödinger’s equation for a particle in a one-dimensional box that there is a set of solutions, the stationary states, for which the time dependence is just an overall rotating phase factor, and these solutions correspond to definite values of the energy. An alternative way of finding that set of solutions is separation of variables. The basic strategy is to assume that the solution to the wave equation can be factored into a product of two functions, one depending only on time, the other on the spatial variable,

$ψ (x, t) = ψ (x) φ (t) .$

If this solution is substituted in the Schrödinger equation, and the result divided by $ψ (x, t),$ we find

$\frac{i ℏ \frac{\partial φ (t)}{\partial t}}{φ (t)} = \frac{- \frac{ℏ^{2}}{2 m} \frac{\partial ψ (x)}{\partial x} + V (x) ψ (x)}{ψ (x)} .$

On writing the equation in this form, it is clear that the left hand side is only a function of t, not of x, and the right hand side is only a function of x! This can only make sense if in fact both sides are the same constant. If we denote this constant by E, we can write two equations:

$\begin{array}{l} i ℏ \frac{\partial φ (t)}{\partial t} = E φ (t) \\ - \frac{ℏ^{2}}{2 m} \frac{\partial^{2} ψ (x)}{\partial x^{2}} + V (x) ψ (x) = E ψ (x) . \end{array}$

The solution to the first equation just gives the phase time dependence,

$φ (t) = A e^{- \frac{i E t}{ℏ}}$

and the second is the time independent Schrödinger equation as before. The solutions to this equation are determined by the boundary conditions on $ψ,$ in general there is a sequence of such eigenstates labeled by a quantum number $n = 0, 1, 2, 3, \dots$ with corresponding values which are put in the corresponding $φ (t) .$

A Two Dimensional Box

Let us now consider the Schrödinger equation for an electron confined to a two dimensional box, $0 < x < a, 0 < y < b .$ That is to say, within this rectangle the electron wave function behaves as a free particle ( $V (x, y) = 0$ ), but the walls are impenetrable so the wave function $ψ (x, y, t) = 0$ at the walls. What do we expect the wave function to look like?

First notice that the separation of variables trick given above for one dimension works equally well here, writing $ψ (x, y, t) = ψ (x, y) φ (t)$ gives

$\begin{array}{l} i ℏ \frac{\partial φ (t)}{\partial t} = E φ (t) \\ - \frac{ℏ^{2}}{2 m} (\frac{\partial^{2} ψ (x, y)}{\partial x^{2}} + \frac{\partial^{2} ψ (x, y)}{\partial y^{2}}) = E ψ (x, y) . \end{array}$

The surprising thing at this point is that we can do the separation of variables trick again $—$ we can write $ψ (x, y) = f (x) g (y)$ and substitute in the above equation to find

$- \frac{ℏ^{2}}{2 m} (\frac{\frac{\partial^{2} f (x)}{\partial x^{2}}}{f (x)} + \frac{\frac{\partial^{2} g (y)}{\partial y^{2}}}{g (y)}) = E .$

Again, we have an equation in which only one term is x-dependent, so it must be a constant (which we take to be negative for future convenience),

$\frac{\frac{\partial^{2} f (x)}{\partial x^{2}}}{f (x)} = - C, say, so \frac{\partial^{2} f (x)}{\partial x^{2}} = - C f (x) .$

This is exactly the same equation we dealt with in the one dimensional case, so we know

$f (x) = A \sin \frac{n π x}{a}$

with $n$ an integer, and the constant $C$ is equal to $n^{2} π^{2} / a^{2} .$ Hence the energy levels in this rectangular well are given by

$E_{n, m} = \frac{ℏ^{2}}{2 m} (\frac{n^{2} π^{2}}{a^{2}} + \frac{m^{2} π^{2}}{b^{2}})$

with $n, m$ the two quantum numbers needed to label each state.

Degenerate States

Two distinct wave functions are said to be degenerate if they correspond to the same energy. If the sides $a, b$ of the rectangle are such that $a / b$ is irrational (the general case), there will be no degeneracies. The most degenerate case is the square, $a = b,$ for which clearly $E_{m, n} = E_{n, m} .$ Degeneracies in quantum physics are most often associated with symmetries in this way.

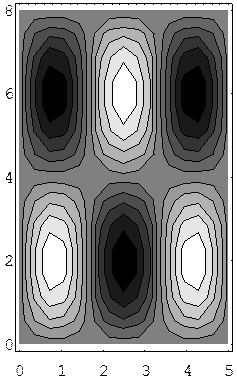
We give here examples of wave functions (3,2) and (2,3) for a rectangle. These are contour maps for the time-independent solution, with white being the highest point. These two wave functions do not correspond to the same energy, although they would, of course, for a square.

A 2D Circular Well

There is a well-known (scanning tunneling microscope) picture of a “corral” of 48 iron atoms arranged in a circle on a flat surface. The picture suggests that there are local electron states in the corral, there are concentric rings of electron density inside (but not outside) the atomic ring.

Let us assume the situation is well described by $V (r) = 0 for r < a,$ $V (r) = \infty for r \geq a .$ It is convenient to write the time independent Schrödinger equation in the form

$(\nabla^{2} + k^{2}) ψ = 0, where k^{2} = \frac{2 m E}{ℏ^{2}} .$

Since the system we are analyzing has circular symmetry, it is natural to try for a solution by separating variables

$ψ (r, θ) = R (r) Θ (θ) .$

Expressing $\nabla^{2}$ in $(r, θ)$ coordinates, Schrödinger’s equation in zero potential becomes:

$\frac{1}{r} \frac{\partial}{\partial r} (r \frac{\partial ψ}{\partial r}) + \frac{1}{r^{2}} \frac{\partial^{2} ψ}{\partial θ^{2}} + k^{2} ψ = 0.$

Substituting the factored wave function $ψ (r, θ) = R (r) Θ (θ)$ in this equation, and dividing by $ψ$ as before, gives the two equations:

$\begin{array}{l} \frac{d^{2} Θ (θ)}{d θ^{2}} = - m^{2} Θ (θ) \\ \frac{d^{2} R (r)}{d r^{2}} + \frac{1}{r} \frac{d R (r)}{d r} + (k^{2} - \frac{m^{2}}{r^{2}}) R (r) = 0. \end{array}$

The constant term that arises when a function of $r$ is equal to a function of $θ$ we set equal to $m^{2},$ for reasons that are immediately apparent on examining the $θ$ -equation above. The solutions to this equation are just $e^{i m θ} and e^{- i m θ},$ and will be single valued only if $m$ is an integer. Thus the quantum number $m$ gives the number of oscillations of the wave function on going in a path around the origin. This is strongly reminiscent of the de Broglie interpretation of the Bohr quantum condition.

The equation for the radial function $R (r)$ is actually a well-known equation in mathematical physics, it is Bessel’s equation. (The two equations together describe vibrations of a circular drumhead, or waves on the surface of a cup of coffee.) We must then solve Bessel’s equation subject to the requirements that the function vanish at $r = a$ (the wall) and also that it be finite at $r = 0$ (the $1 / r^{2}$ term in the last bracket means that not all solutions of Bessel’s equation satisfy this condition). Fortunately, Bessel’s equation has been thoroughly explored, and we can just look up solutions.

previous home next