One Dimensional Finite Depth Square Well

Michael Fowler, University of Virginia

Introduction

We have considered in some detail a particle trapped between infinitely high walls a distance $L$ apart, we found the wave function solutions of the time independent Schrödinger equation, and the corresponding energies. The essential point was that the wave function had to go to zero at the walls, because there is zero probability of finding the particle penetrating an infinitely high wall. This meant that the lowest energy state couldn't have zero energy (meaning the potential energy at the flat bottom of the well). Rather, the lowest energy state had to have the minimal amount of bending of the wave function necessary for it to be zero at the two walls but nonzero in between $—$ this corresponds to half a period of a sine or cosine (depending on the choice of origin), these functions being the solutions of Schrödinger's equation in the zero potential region between the walls. The sequence of wave functions (eigenstates) as the energy increases have 0, 1, 2, … zeros (nodes) in the well.

Let us now consider how this picture is changed if the potential at the walls is not infinite. It will turn out to be convenient to have the origin at the center of the well, so we take

$\begin{array}{l} V (x) = V_{0}, x \leq - L / 2, \\ V (x) = 0, - L / 2 < x < L / 2, \\ V (x) = V_{0}, L / 2 \leq x . \end{array}$

Having the potential symmetric about the origin makes it easier to catalog the wave functions. For a symmetric potential, the wave functions can always be taken to be symmetric or antisymmetric. If a wave function $ψ (x)$ is a solution of Schrödinger's equation with energy $E,$ and the potential is symmetric, then $ψ (- x)$ is a solution with the same energy. This means that $ψ (x) + ψ (- x)$ and $ψ (x) - ψ (- x)$ are also solutions, since the equation is linear, and these are symmetric and antisymmetric respectively, and using them is completely equivalent to using the original $ψ (x)$ and its reflection $ψ (- x) .$

How is the lowest energy state wave function affected by having finite instead of infinite walls? Inside the well, the solution to Schrödinger's equation is still of cosine form (it's a state symmetric about the origin). However, since the walls are now finite, $ψ (x)$ cannot change slope discontinuously to a flat line at the walls. It must instead connect smoothly with a function which is a solution to Schrödinger's equation inside the wall.

The equation in the wall is

$- \frac{ℏ^{2}}{2 m} \frac{d^{2} ψ (x)}{d x^{2}} + V_{0} ψ (x) = E ψ (x)$

and has two exponential solutions (say for $x \geq L / 2$ ) one increasing to the right, the other decreasing,

$e^{α x} and e^{- α x}, where α = \sqrt{2 m (V_{0} - E) / ℏ^{2}} .$

(We are assuming here that $E < V_{0},$ so the particle is bound to the well. We shall find this is always true for the lowest energy state.)

Let us try to construct the wave function for the energy $E$ corresponding to this lowest bound state. From the equation with $V_{0} = 0,$ the wavefunction inside the well (let's assume it's symmetric for now) is proportional to $\cos k x,$ where $k = \sqrt{2 m E / ℏ^{2}} .$

The wave function (and its derivative!) inside the well must match a sum of exponential terms $—$ the wave function in the wall $—$ at $x = L / 2,$ so

$\begin{matrix} \cos (k L / 2) = A e^{α L / 2} + B e^{- α L / 2} \\ - k \sin (k L / 2) = α A e^{α L / 2} - α B e^{- α L / 2} . \end{matrix}$

(By writing just a cosine term inside the well, we have left out the overall normalization constant. This can be put back in at the end.)

Solving these equations for the coefficients $A, B$ in the usual way, we find that in general the cosine solution inside the well goes smoothly into a linear combination of exponentially increasing and decreasing terms in the wall. (By the symmetry of the problem, the same thing must happen for $x < - L / 2.$ )

However, this cannot in general represent a bound state in the well. The increasing solution increases without limit as $x$ goes to infinity, so since the square of the wave function is proportional to the probability of finding the particle at any point, the particle is infinitely more likely to be found at infinity than anywhere else. It got away! This clearly makes no sense $—$ we're trying to find wave functions for particles that stay in, or at least close to, the well. We are forced to conclude that the only exponential wave function that makes sense is the one for which $A$ is exactly zero, so that there is only a decreasing wave in the wall.

Requiring the decreas ing wave function, $A = 0,$ means that only a discrete set of values of $k,$ or $E,$ satisfy the boundary condition equations above. They are most simply found by taking $A = 0$ and dividing one equation by the other to give:

$\tan (k L / 2) = α / k .$

This cannot be solved analytically, but is easy to solve graphically by plotting the two sides as functions of $k$ (recall $α = \sqrt{2 m (V_{0} - E) / ℏ^{2}},$ and $k = \sqrt{2 m E / ℏ^{2}}$ ) and finding where the curves intersect.

Solving Schrödinger's Equation Numerically

A more straightforward approach is to solve the Schrödinger equation numerically, using a spreadsheet, and explore how the wave function varies as $E$ is changed. This method has the great advantage that the spreadsheet can be readily adapted to any reasonable potential. We present first the simplest, least sophisticated method, which gives an accuracy of around one percent for energy values using a few hundred rows of the spreadsheet.

To simplify adapting the spreadsheet to the equation, we choose units so that $ℏ^{2} / 2 m = 1.$

From now on, in this section we shall denote the wave function by f(x) or just f instead of ψ(x) , to lessen headaches in setting up the spreadsheet.

Schrödinger's Equation is then:

$\frac{d^{2} f (x)}{d x^{2}} = (V (x) - E) f (x) .$

To solve this using the spreadsheet, it is necessary to discretize the derivative. We replace the continuous variable x by a sequence of equally spaced points dx apart, such as 0, dx, 2dx, 3dx, … . Here dx is of course finite, we should really call it Δx.

We approximate the second derivative by:

${(\frac{d^{2} f (x)}{d x^{2}})}_{x = x_{j}} = \frac{f (x_{j + 1}) - 2 f (x_{j}) + f (x_{j - 1})}{{(d x)}^{2}}$

so the differential equation is replaced by the difference equation:

$\frac{f (x_{j + 1}) - 2 f (x_{j}) + f (x_{j - 1})}{{(d x)}^{2}} = (V (x_{j}) - E) f (x_{j}) .$

Notice that from this equation, if we know f(x_j), f(x_j_-1) and V(x_j) we can find f(x_j₊₁). Of course, we do know V(x_j), this is the potential we are trying to solve for. We can also specify E, the energy of the particle, although we shall find that for negative E, only a discrete set of bound state energies correspond to normalizable wave functions.

A second-order differential equation like this needs two boundary conditions for the solution to be defined. We can specify the initial value of f and its derivative df/dx. But this is just equivalent to giving the first two members of the discrete series, f(x₀) and f(x₁), say. We can then use the difference equation to find f(x₂), then use it again to find f(x₃) and so on. This is what the spreadsheet does for us: we find f(x_j₊₁) row by row using the difference equation above written:

$f (x_{j + 1}) = (2 + {(d x)}^{2} (V (x_{j}) - E)) f (x_{j}) - f (x_{j - 1}) .$

Using the Spreadsheet for the Finite Square Well

Recall that by taking the origin in the center of the square well, we argued that we need only look at wave functions that were symmetric or antisymmetric about the origin. If you try to sketch such wave functions, you will find that symmetric wave functions must have zero slope at the origin, and antisymmetric wave functions must be zero at the origin.

Furthermore, if we know the wave function in the right-hand half, that is, for x > 0, we know it for all x, from the symmetry. Hence, we need only solve Schrödinger's equation going from the origin to the right - we can take x₀ = 0, x₁ = dx, etc.

As we discussed in the preceding section, on integrating out from the origin with energy E set less than V₀, once we cross over into the wall the solution is some combination of an exponentially increasing function and an exponentially decreasing function,

$f (x) = A (E) e^{α x} + B (E) e^{- α x}$

where the exponential coefficient α is positive, and depends on E $—$ it was defined in the preceding section.

Let us first look at the symmetric solutions for very low energies, so take f(0) = 1, f'(0) =0. (Note that we cannot find the correct overall normalization constant until we find the solution, then integrate its square over all space $—$ this can always be done later, and is unnecessary for analyzing the properties of the state).

Let us begin with the trivial case E = 0. For zero energy, inside the well E - V will of course be identically zero, so from Schrödinger's equation the slope of f(x) can never change, consequently f(x) = 1 for all x < L. On reaching the wall, this wave function and its derivative connect smoothly from inside to outside if A = B = $½$ . It is clear that as we keep going to the right, the A term in the above equation dominates and f(x) diverges, signaling that there is no state localized in the well at E = 0.

At this point, you should create an Excel spreadsheet, with a graph showing f(x) and V(x)-E as functions of x. Details of how this might be done are given in the accompanying homework assignment. If you have a working spreadsheet, it will be much easier to understand the following discussion!

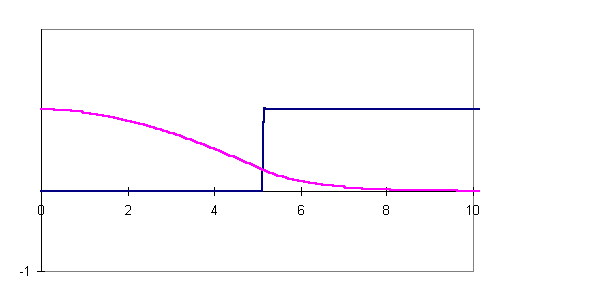
As we now increase E from zero, the symmetric wave function, having zero slope at the center of the well, will begin to curve downwards on moving away from the center, and as the energy increases so does the downward curvature. This naturally changes the mix of increasing and decreasing exponentials needed to connect smoothly at the wall, and in fact as a function of E, A(E) changes sign at a certain value we will call E₀. For energies just below E₀, f(x) diverges to plus infinity for large x. For energies above E₀, it diverges to minus infinity for large x. Exactly at E₀, f(x) goes to zero for large x. This is the wave function we are looking for: it corresponds to a particle localized close to the well, and in fact is the lowest possible energy $—$ the ground state $—$ for a particle in the well. E₀ is called the ground state eigenvalue, the wave function is called an eigenstate.

Finding the Ground State Energy

The first problem is to find this value E₀. If we just guess a value of E, the wave function will almost certainly diverge for large x. The way to find E₀ is to notice that for E below E₀, f(x) goes to large positive values on the far right, for E just above E₀, f(x) goes to large negative values on the far right. So we take an increasing set of E values starting near zero, and watch for the tail to wag! When this happens, we back up half way, then back or forward as necessary, choosing a set of E values that bracket E₀.

Actually, this rather tedious process can be automated in Excel, but it's worth going through it manually a time or two to get a feeling for how the wave functions behave. A general feature to check is that for E > V(x) they are oscillatory, sine or cosine like, although with changing wavelengths in general; whereas for E < V(x) they have exponential character. You can see why this is by looking at the equation, but it’s worth bearing in mind as you examine the curves.

Automating the Process

Now to a bit of automation. The strategy we are following is to adjust E until the function f(x) goes to zero for large x, that is, far down at the bottom of our column having several hundred entries. Since we would like to know how well we are doing, it’s convenient to have the spreadsheet copy that value to some cell near the top. So, if the end of our column of f(x_i)'s is F600, say, then we enter =$F$600 in some convenient square near the top, say B22. Now we can keep an eye on the distant value as we adjust E. We can also get Excel to do this for us as follows (I assume the value of E is entered into square B15):

Click Tools, Goal Seek. Then fill out the dialog box: Set Cell B22 to value 0 by changing cell B15. (You can fill in the cell addresses by just clicking on the appropriate cells.) Click OK. It will then calculate and come up with a value. Click OK again.

The curve below was generated by this procedure. It is worth noting that there is a definite probability of finding the particle inside the wall, that is to say, the wave function is nonzero there (and, it turns out, for reasonable, physical values of the parameters):

All square well potentials in one dimension, however shallow, have a localized ground state with this general shape. Whether or not there are other eigenstates with other eigenvalues depends on the depth of the potential. For a sufficiently shallow potential, there is only one state. An infinitely deep well, as we discussed earlier, has an infinite number of bound states. As the well depth increases from zero, states are bound sequentially. These higher eigenstates are called excited states. A particle in one of them will usually decay to a lower state, emitting a photon, just as in the Bohr atom.

Finding Excited States

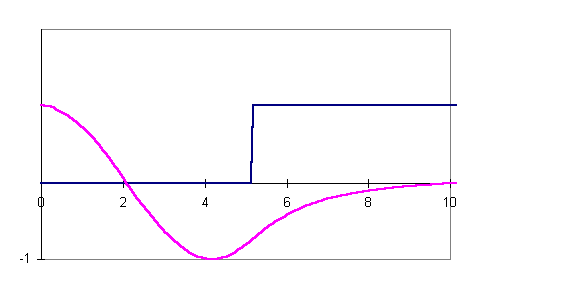
Let us now see how the wave function develops as E increases beyond E₀ for a sufficiently deep well. As the energy is increased, the cosine term inside the well has tighter curvature, and the exponentially increasing term for large x is large and negative. However, continuing to increase the energy, eventually the cosine term bottoms out inside the well and begins to turn up again before reaching the wall. At a certain energy, it again becomes possible to match it to a decreasing function:

To find this new eigenvalue, we can get close to it then use: Tools, Goal Seek just as we did for the ground state $—$ see above.

Creating a Macro

To really automate this procedure, it's worth creating a macro. So, go to Tools, Record Macro, Record New Macro. Call the Macro "Eigenvalue", and put in the shortcut Ctrl+e. In the Record Macro box, click OK to begin recording. Then Click Tools, Goal Seek. Then fill out the dialog box just as we did before, that is, Set Cell B22 to value 0 by changing cell B15. Click OK. It will then calculate and come up with a value. Click OK again. That is all we want to record, so click Tools, Macro, Stop Recording.

You can check to see if your macro is working by changing the value of E in B15, then hit Ctrl+e. (If you forgot to assign the shortcut to your macro, you can do it now by clicking Tools, Macro, Macros, click on your macro and click Options. You can fill in the shortcut key in the Options box.)

To get really fancy, it’s nice to run this macro by clicking on something. Insert a textbox somewhere in your spreadsheet, and write “Find Eigenvalue” on it. With the textbox selected, right click on one of the sizing handles and click “Assign Macro” . Choose your “Eigenvalue” macro. Now it will run if you click on the textbox.

A point to notice about the wave function pictured above is that has a node at about x = 2. (Actually, of course, this is just half the wave function for the complete well-there will be another node at x = -2.) As we continue to increase E, the high-x tail of the wave function wags up and down. Each time it crosses the axis there is an allowable wave function. Furthermore, each time it crosses the axis the wave function collects another node for x > 0. Thus, the complete wave functions generated by this method have 0, 2, 4, 6, … nodes. From the symmetry of the problem, the allowable wave functions with an odd number of nodes must have one node at the origin. They can be generated by taking as initial conditions that f is zero at the origin, and has finite slope.

Curvature of Wave Functions

Schrödinger's equation in the form

$\frac{d^{2} f (x)}{d x^{2}} = (V (x) - E) f (x)$

can be interpreted by saying that the left-hand side, the rate of change of slope, is the curvature $—$ so the curvature of the function is equal to (V(x) - E)f(x). This means that if E > V(x), for f(x) positive f(x) is curving negatively, for f(x) negative f(x) is curving positively. In both cases, f(x) is always curving towards the axis. This means that for E > V(x), f(x) has a kind of stability: its curvature is always bringing it back towards the axis, so it has oscillatory character.

On the other hand, for V(x) > E, the curvature is always away from the axis. This means that f(x) tends to diverge to infinity. Only under exactly the right conditions will this curvature be just enough to bring the wave function to zero as x goes to infinity. (As f(x) tends to zero, the curvature tends to zero, too.)

It is worth examining the wave functions generated by the spreadsheet to see just how the curvature changes as V(x) - E, or for that matter f(x), changes sign.

previous home next