Rutherford Scattering

Michael Fowler, University of Virginia

Rutherford as Alpha-Male

[Rutherford was] a "tribal chief", as a student said.

(Richard Rhodes, The Making of the Atomic Bomb, page 46)

In 1908 Rutherford was awarded the Nobel Prize—for chemistry! The award citation read: "for his investigations into the disintegration of the elements, and the chemistry of radioactive substances." While at McGill University, he had discovered that the radioactive element thorium emitted a gas which was itself radioactive, but if the gas radioactivity was monitored separately from the thorium's, he found it decreased geometrically, losing approximately half its current strength for each minute that passed. The gas he had found was a short-lived isotope of radon, and this was the first determination of a "half-life" for a radioactive material. (Pais, Inward Bound, page 120).

The chemists were of course impressed that Rutherford was fulfilling their ancient alchemical dream of transmuting elements, or at least demonstrating that it happened. Rutherford himself remarked at the ceremony that he "had dealt with many different transformations with various time-periods, but the quickest he had met was his own transformation from a physicist to a chemist". Still, Nobel prizes of any kind are nice to get, so he played along, titling his official Nobel lecture: "The chemical nature of the alpha-particle from radioactive substances". (He established that his favorite particle was an ionized helium atom by collecting alphas in an evacuated container, where they picked up electrons. After compressing this very rarefied gas, he passed an electric discharge through it and observed the characteristic helium spectrum in the light emitted.)

Rutherford was the world leader in alpha-particle physics. In 1906, at McGill University, Montreal, he had been the first to detect slight deflections of alphas on passage through matter. In 1907, he became a professor at the University of Manchester, where he worked with Hans Geiger. This was just a year after Rutherford's old boss, J. J. Thomson, had written a paper on his plum pudding atomic model suggesting that the number of electrons in an atom was about the same as the atomic number. (Not long before, people had speculated that atoms might contain thousands of electrons. They were assuming that the electrons contributed a good fraction of the atom's mass.) The actual distribution of the electrons in the atom, though, was as mysterious as ever. Mayer's floating magnets (see previous lecture) were fascinating, but had not led to any quantitative conclusions on electronic distributions in atoms.

Rutherford's 1906 discovery that his pet particles were slightly deflected on passing through atoms came about when he was finding their charge to mass ratio, by measuring the deflection in a magnetic field. He detected the alphas by letting them impact photographic film. When he had them pass through a thin sheet of mica before hitting the film (so the film didn't have to be in the vacuum?) he found the image was blurred at the edges, evidently the mica was deflecting the alphas through a degree or two. He also knew that the alphas wouldn't be deflected a detectable amount by the electrons in the atom, since the alphas weighed 8,000 times as much as the electrons, atoms contained only a few dozen electrons, and the alphas were very fast. The mass of the atom must be tied up somehow with the positive charge. Therefore, he reasoned, analyzing these small deflections might give some clue as to the distribution of positive charge and mass in the atom, and therefore give some insight into his old boss J. J.'s plum pudding. The electric fields necessary in the atom for the observed scattering already seemed surprisingly high to Rutherford (Pais, page 189).

Scattering Alphas

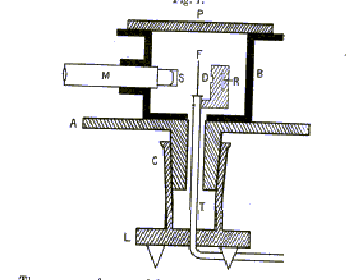
Rutherford's alpha scattering experiments were the first experiments in which individual particles were systematically scattered and detected. This is now the standard operating procedure of particle physics. To minimize alpha loss by scattering from air molecules, the experiment was carried out in a fairly good vacuum, the metal box being evacuated through a tube T (see below). The alphas came from a few milligrams of radium (to be precise, its decay product radon 222) at R in the figure below, from the original paper, which goes on:

"By means of a diaphragm placed at D, a pencil of alpha particles was directed normally on to the scattering foil F. By rotating the microscope [M] the alpha particles scattered in different directions could be observed on the screen S."

Actually, this was more difficult than it sounds. A single alpha caused a slight fluorescence on the zinc sulphide screen S at the end of the microscope. This could only be reliably seen by dark-adapted eyes (after half an hour in complete darkness) and one person could only count the flashes accurately for one minute before needing a break, and counts above 90 per minute were too fast for reliability. The experiment accumulated data from hundreds of thousands of flashes.

Rutherford's partner in the initial phase of this work was Hans Geiger, who later developed the Geiger counter to detect and count fast particles. Many hours of staring at the tiny zinc sulphide screen in the dark must have focused his mind on finding a better way!

In 1909, an undergraduate, Ernest Marsden, was being trained by Geiger. To quote Rutherford (a lecture he gave much later):

"I had observed the scattering of alpha-particles, and Dr. Geiger in my laboratory had examined it in detail. He found, in thin pieces of heavy metal, that the scattering was usually small, of the order of one degree.

"One day Geiger came to me and said, "Don't you think that young Marsden, whom I am training in radioactive methods, ought to begin a small research?" Now I had thought that, too, so I said, " Why not let him see if any alpha-particles can be scattered through a large angle?"

"I may tell you in confidence that I did not believe that they would be, since we knew the alpha-particle was a very fast, massive particle with a great deal of energy, and you could show that if the scattering was due to the accumulated effect of a number of small scatterings, the chance of an alpha-particle's being scattered backward was very small. Then I remember two or three days later Geiger coming to me in great excitement and saying "We have been able to get some of the alpha-particles coming backward …" It was quite the most incredible event that ever happened to me in my life. It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you."

Disproof of the Pudding

The back scattered alpha-particles proved fatal to the plum pudding model. A central assumption of that model was that both the positive charge and the mass of the atom were more or less uniformly distributed over its size, approximately 10^-10 meters across or a little more. It is not difficult to calculate the magnitude of electric field from this charge distribution. (Recall that this is the field that must scatter the alphas, the electrons are so light they will jump out of the way with negligible impact on an alpha.)

To be specific, let us consider the gold atom, since the foil used by Rutherford was of gold, beaten into leaf about 400 atoms thick. The gold atom has a positive charge of 79e (balanced of course by that of the 79 electrons in its normal state). Neglect the electrons—they'll be scattered away with negligible impact on the heavy alpha.

See the animation here!

The maximum electric force the alpha will encounter is that at the surface of the sphere of positive charge,

$E \cdot 2 e = \frac{1}{4 π ε_{0}} \cdot \frac{79 e \cdot 2 e}{r_{0}^{2}} = 9 \cdot 10^{9} \frac{158 \cdot (1.6 \cdot 10^{- 19})}{10^{- 20}} = 3.64 \cdot 10^{- 6} Newtons .$

(In this model, once inside the sphere the electric force goes down, just as gravity goes down on going deep into the earth, to zero at the center. But the sideways component stays approximately constant if the path is nearly a straight line.)

If the alpha particle initially has momentum $p,$ for small deflections the angle of deflection (in radians) is given by $Δ p / p,$ where $Δ p$ is the sideways momentum resulting from the electrically repulsive force of the positive sphere of charge.

A good estimate of the sideways deflection is given by taking the alpha to experience the surface force given above for a time interval equal to the time it takes the alpha to cross the atom—say, a distance $2 r_{0} .$ (The force felt when outside the ball of charge is much smaller: it drops away as the inverse square, but at an angle that makes it effectively inverse cube. It can be shown to make only a small contribution.)

Note that since the alpha particle has mass 6.7x10^-27 kg, from $F = m a,$ the electric force at the atomic surface above will give it a sideways acceleration of 5.4x10²⁰ meters per sec per sec (compare $g = 10$ !). But the force doesn't have long to act—the alpha is moving at 1.6x10⁷ meters per second. So the time available for the force to act is the time interval a particle needs to cross an atom if the particle gets from New York to Australia in one second.

So the transit time for the alpha across the plum pudding atom is:

$t_{0} = 2 r_{0} / v = 2 \times 10^{10} / 1.6 \times 10^{7} = 1.25 \times 10^{- 17} seconds .$

Now, the magnitude of the total sideways velocity picked up on crossing the atom is the sideways acceleration multiplied by the time,

$1.25 \times 10^{- 17} \times 5.4 \times 10^{20} = 6750 m /sec .$

This is a few ten-thousandths of the alpha's forward speed, so there is only a very tiny deflection. Even if the alpha hit 400 atoms in succession and they all deflected it the same way, an astronomically improbable event, the deflection would only be of order a degree. Therefore, the observed deflection throughninety degrees and more was completely inexplicable using Thomson's pudding model!

Emergence of the Nucleus

Rutherford pondered the problem for some months. He had been a believer in his former boss's pudding model, but he eventually decided there was simply no way it could generate the strength of electric field necessary to deflect the fast moving alphas. Yet it was difficult to credit there was much more positive charge around than that necessary to compensate for the electrons, and it was pretty well established that there were not more than a hundred or so electrons (we used 79, the correct value—that was not known exactly until a little later). The electric field from a sphere of charge reaches its maximum on the surface, as discussed above. Therefore, for a given charge, assumed spherically distributed, the only way to get a stronger field is tocompress it into a smaller sphere. Rutherford concluded that he could only explain the large alpha deflections if the positive charge, and most of the mass of the atom, was in a sphere much smaller than the atom itself.

It is not difficult to estimate from the above discussion how small such a nucleus would have to be to give a substantial deflection. We found a sphere of radius 10^-10 meters gave a deflection of about 4x10^-4 radians. We need to increase this deflection by a factor of a few thousand. On decreasing the radius of the sphere of positive charge, the force at the surface increases as the inverse radius squared. On the other hand, the time over which the alpha experiences the sideways force decreases as the radius.

The total deflection, then, proportional to the product of force and time, increases as the inverse of the radius. This forces the conclusion that the positive charge is in a sphere of radius certainly less than 10^-13 meters, provided all the observed scattering is caused by one encounter with a nucleus.

Animation of scattering from a nuclear atom here!

Rutherford decided that the observed scattering was in fact from a single nucleus. He argued as follows: since the foil is only 400 atoms thick, it is difficult to see how ninety degree scatterings could arise unless the scattering by a single nucleus was at least one degree, say 100 times that predicted by the Thomson model. This would imply that the nucleus had a radius at most one-hundredth that of the atom, and therefore presented a target area for one-degree scattering (or more) to the incoming alphas only one ten-thousandth that of the atom. (In particle physics jargon, this target area is called the scattering cross section.) If an alpha goes through 400 layers of atoms, and in each layer it has a chance of one in ten thousand of getting close enough to the nucleus for a one-degree scatter, this is unlikely to happen twice. It follows that almost certainly only one scattering takes place. It then follows that all ninety or more degrees of scattering must be a single event, so the nucleus must be even smaller than one hundredth the radius of the atom -- it must be less than 10^-13 meters, as stated above.

Seeing the Nucleus

Having decided that the observed scattering of the alphas came from single encounters with nuclei, and assuming that the scattering force was just the electrostatic repulsion, Rutherford realized maybe just scaling down the radius in the plum pudding analysis given above wasn't quite right. Maybe the nucleus was so small that the alpha particle didn't even touch it. If that were the case, the alpha particle's entire trajectory was determined by a force law of inverse square repulsion, and could be analyzed precisely mathematically by the techniques already well-known to astronomers for finding paths of planets under inverse square attraction.

It turns out that the alpha will follow a hyperbolic path (see the animation). Imagine an alpha coming in along an almost straight line path, the perpendicular distance of the nucleus from this line is called the impact parameter (how close to the center the alpha particle would pass if the repulsion were switched off). The standard planetary math is enough to find the angle at which the alpha comes out (the scattering angle), given the impact parameter and speed. Although not exactly a hot shot theorist, Rutherford managed to figure this out after a few weeks.

The incoming stream of alphas all have the same velocity (including direction) , but random impact parameters: we assume the beam intensity doesn't vary much in the perpendicular direction, certainly on an atomic scale, so we average over impact parameters (with a factor $2 π p d p$ for the annular region $p, p + d p$ ).

The bottom line is that for a nucleus of charge $Z,$ and incident alpha particles of mass $m$ and speed $v,$ the rate of scattering to a point on the screen corresponding to a scattering angle of $θ$ (angle between incident velocity and final velocity of alpha) is proportional to:

$scattering into small area at θ \propto {(\frac{1}{4 π ε_{0}} \cdot \frac{Z e^{2}}{m v^{2}})}^{2} \cdot \frac{1}{\sin^{4} (θ / 2)} .$

Analysis of the hundred thousand or more scattering events recorded for the alphas on gold fully confirmed the angular dependence predicted by the above analysis.

Modeling the Scattering

To visualize the path of the alpha in such a scattering, Rutherford "had a model made, a heavy electromagnet suspended as a pendulum on thirty feet of wire that grazed the face of another electromagnet set on a table. With the two grazing faces matched in polarity and therefore repelling each other, the pendulum was deflected" into a hyperbolic path.(Rhodes, page 50)

But it didn't work for Aluminum...

On replacing the gold foil by aluminum foil (some years later), it turned out that small angle scattering obeyed the above law, but large angle scattering didn't. Rutherford correctly deduced that in the large angle scattering, which corresponded to closer approach to the nucleus, the alpha was actually hitting the nucleus. This meant that the size of the nucleus could be worked out by finding the maximum angle for which the inverse square scattering formula worked, and finding how close to the center of the nucleus such an alpha came. Rutherford estimated the radius of the aluminum nucleus to be about 10^-14 meters.

The Beginnings of Nuclear Physics

The First World War lasted from 1914 to 1918. Geiger and Marsden were both at the Western front, on opposite sides. Rutherford had a large water tank installed on the ground floor of the building in Manchester, to carry out research on defense against submarine attack. Nevertheless, occasional research on alpha scattering continued. Scattering from heavy nuclei was fully accounted for by the electrostatic repulsion, so Rutherford concentrated on light nuclei, including hydrogen and nitrogen. In 1919, Rutherford established that an alpha impinging on a nitrogen nucleus can cause ahydrogen atom to appear! Newspaper headlines blared that Rutherford had "split the atom". (Rhodes, page 137)

Shortly after that experiment, Rutherford moved back to Cambridge to succeed J. J. Thomson as head of the Cavendish laboratory, working with one of his former students, James Chadwick, who had spent the war years interned in Germany. They discovered many unusual effects with alpha scattering from light nuclei. In 1921, Chadwick and co-author Bieler wrote: "The present experiments do not seem to throw any light on the nature of the law of variation of the forces at the seat of an electric charge, but merely show that the forces are of great intensity … It is our task to find some field of force which will reproduce these effects." I took this quote from Pais, page 240, who goes on to say that he considers this 1921 statement as marking the birth of the strong interactions.

In fact, Rutherford was beginning to focus his attention on the actual construction of the nucleus and the alpha particle. He coined the word "proton" to describe the hydrogen nucleus, it first appeared in print in 1920 (Pais). At first, he thought the alpha must be made up of four of these protons somehow bound together by having two electrons in the middle—this would get the mass and charge right, but of course nobody could construct a plausible electrostatic configuration. Then he had the idea that maybe there was a special very tightly bound state of a proton and an electron, much smaller than an atom. By 1924, he and Chadwick were discussing how to detect this neutron. It wasn't going to be easy—it probably wouldn't leave much of a track in a cloud chamber. In fact, Chadwick did discover the neutron, but not until 1932, and it wasn't much like their imagined proton-electron bound state. But it did usher in the modern era in nuclear physics.

previous home next