Transforming Energy into Mass: Particle Creation

Michael Fowler, University of Virginia

Relativistic Collisions Can Produce New Particles

We have mentioned how, using a synchrocyclotron, it is possible to accelerate protons to relativistic speeds. The rest energy of a proton $m_{p} c^{2}$ is 938 MeV, using here the standard high energy physics energy unit: 1 MeV = 10⁶ eV. The neutron is a bit heavier— $m_{n} c^{2} = 940$ MeV. (The electron is 0.51 MeV). Thus to accelerate a proton to relativistic speeds implies giving it a K.E. of order 1,000 MeV, or 1 GeV.

The standard operating procedure of high energy physicists is to accelerate particles to relativistic speeds, then smash them into other particles to see what happens. For example, fast protons will be aimed at protons at rest (hydrogen atoms, in other words—the electron can be neglected). In a collider, beams of accelerated protons have head-on collisions. As we shall see, this greatly increases the center of mass energy (it's not just doubled) but of course the number of hits goes down a lot.

To see what results from the collision, the resulting debris (usually flying away fast!) must be detected. The first successful detector was the cloud chamber, invented in 1911. If a fast charged particle flies through a supersaturated gas, it ionizes some molecules, they are then nuclei or seeds for droplet formation, and the path is realized as a string of tiny drops. The cloud chamber was superseded in the fifties by the bubble chamber, a transparent container filled with a superheated liquid. an energetic particle moving through the liquid leaves a trail of ionized molecules, which nucleate bubbles. The bubbles grow rapidly to highlight the path, then rise and go away far faster than the droplets in the cloud chamber. But as accelerators developed, and began searching for less frequent events, faster and faster turnaround times became essential for the detectors. Clouds and bubbles were replaced by sparks and wires, fine parallel wires millimeters apart, in an easily ionized gas, the passing particle generating sparks between the wires. This improved response time by orders of magnitude. Nowadays, detectors often consist of many thousands of very tiny solid state reverse biased diodes, triggered by the particle, and wired to give precise trajectory information. In fact, major experiments have the collision area surrounded by layers of both solid state detectors and wire grid detectors.

Anyway, back to the first early attempts, and what was observed—it turned out that in $p - p$ scattering at low but relativistic energies, sometimes more particles came out than went in—particles called pions, π⁺, π⁰, π^- were created. The π⁰ is electrically neutral, the π⁺ has exactly the same amount of charge as the proton. It was found experimentally that total electric charge was always conserved in collisions, no matter how many new particles were spawned, and total baryon number (protons + neutrons) was conserved.

Possible scenarios include:

$p + p \to p + p + π^{0},$

and

$p + p \to p + n + π^{+} .$

The neutral pion mass is 135 MeV, the charged pions have mass 140 MeV, where we follow standard high energy practice in calling mc² the “mass”, since this is the energy equivalent, and hence the energy which, on creation of the particle in a collision, is taken from kinetic energy and stored in mass.

Energy Necessary to Produce a Pion

An incoming proton with 135 MeV of kinetic energy will not be able to create a neutral pion (rest mass 135 Mev) in a collision with a stationary proton. This is because the incoming proton also has momentum, and the collision conserves momentum, so some of the particles after the collision must have momentum and hence kinetic energy.

The simplest way to figure out just how much energy the incoming proton needs to create a neutral pion is to go to the center of mass frame, where initially two protons are moving towards each other with equal and opposite velocities, there being no total momentum. Obviously, in this frame the least possible K.E. must be just enough to create the $π^{0}$ with all the final state particles $(p, p, π^{0})$ at rest. Thus if the the incoming protons in the center of mass frame are traveling at $\pm v,$ the total energy, which must equal the rest energies of the final stationary masses, is

$E = \frac{2 m_{p} c^{2}}{\sqrt{1 - v^{2} / c^{2}}} = 2 m_{p} c^{2} + m_{π} c^{2},$

we find the two incoming protons must both be traveling at 0.36c.

Recall that this is the speed in the center of mass frame, and for practical purposes, like designing the accelerator, we need to know the energy necessary in the “lab” frame—that in which one of the protons is initially at rest. The two frames obviously have a relative speed of 0.36c, so to get the speed of the incoming proton in the lab frame we must add a velocity of 0.36c to one of 0.36c using the relativistic addition of velocities formula, which gives 0.64c. This implies the incoming proton has a relativistic mass of 1.3 times its rest mass, and thus a K.E. around 280 MeV.

Thus to create a pion of rest energy 135 MeV, it is necessary to give the incoming proton at least 290 MeV of kinetic energy. This is called the “threshold energy” for pion production. This “inefficiency” (more energy than seems necessary) arises because momentum must also be conserved, so, in the lab, there is still considerable K.E.in the final particles.

Antiproton Production

On raising the energy of the incoming proton further, more particles are produced, including the “antiproton”—a negatively charged heavy particle which will annihilate a proton in a flash of energy. It turns out experimentally that an antiproton can only be produced accompanied by a newly created proton,

$p + p \to p + p + p + \bar{p} .$

Notice we could have conserved electric charge with less energy with the reaction

$p + p \to p + p + π^{+} + \bar{p}$

but this doesn’t happen—so energy, momentum and charge conservation are not the only constraints in creating new particles. (There's also angular momentum, but that's not important here.)

In fact, what we are seeing here is experimental confirmation that the conservation of baryon number, which at the low energies previously discussed in the context of pion production just meant that the total number of protons plus neutrons stayed fixed, is generalized at high energies to include antiparticles having negative baryon number, -1 for the antiproton. Thus baryon number conservation becomes parallel to electric charge conservation.

New particles can always be produced at high enough energies provided the total new charge and the total new baryon number are both zero. (Actually there are further conservation laws which become important when more exotic particles are produced, we may discuss these later.) We should emphasize again that these are experimental results gathered from examining millions of collisions between relativistic particles.

A Machine Built to Produce One Particle

One of the first modern accelerators, built at >Berkeley in the fifties, was designed specifically to produce the antiproton, so it was very important to calculate that antiproton production threshold correctly! This can be done by the same method we used above for pion production, but we use a different trick here which is often useful. We have shown that on transforming the energy and momentum of a particle from one frame to another

$E^{2} - c^{2} p^{2} = {E^{'}}^{2} - c^{2} {p^{'}}^{2}$

Since the Lorentz equations are linear, if we have a system of particles with total energy E and total momentum p in one frame, E' , p' in another, it must again be true that

$E^{2} - c^{2} {\vec{p}}^{2} = {E^{'}}^{2} - c^{2} {\vec{p^{'}}}^{2} .$

We can use this invariance to get lab frame information from the center of mass frame. Noting that in the center of mass (CM) frame the momentum is zero, and in the lab frame the momentum is all in the incoming proton,

$E_{cm}^{2} = {((m_{in} + m_{0}) c^{2})}^{2} - c^{2} p_{in}^{2}$

where here m₀ is the proton rest mass, $m_{in}$ is the relativistic mass of the incoming proton: we're writing $\frac{m_{0}}{\sqrt{1 - v_{in LAB}^{2} / c^{2}}} = m_{in} .$

At the antiproton production threshold, E_cm = 4m₀c², so

$16 m_{0}^{2} c^{4} = m_{in}^{2} c^{4} + 2 m_{in} c^{2} m_{0} c^{2} + m_{0}^{2} c^{4} - c^{2} p_{in}^{2},$

and using

$m_{in}^{2} c^{4} - c^{2} p_{in}^{2} = m_{0}^{2} c^{4},$

we find

$2 (m_{in} c^{2}) (m_{0} c^{2}) + 2 {(m_{0} c^{2})}^{2} = 16 {(m_{0} c^{2})}^{2}$ ,

$m_{in} c^{2} = 7 m_{0} c^{2}$ .

Therefore to create two extra particles, with total rest energy $2 m_{0} c^{2},$ it is necessary for the incoming proton to have a kinetic energy of $6 m_{0} c^{2} .$ The Berkeley Gevatron had design energy 6.2 GeV.

Higher Energies

As we go to higher energies, this “inefficiency” gets worse—consider energies such that the kinetic energy >> rest energy, and assume the incoming particle and the target particle have the same rest mass, $m_{0},$ with the incoming particle having relativistic mass $m_{in} :$

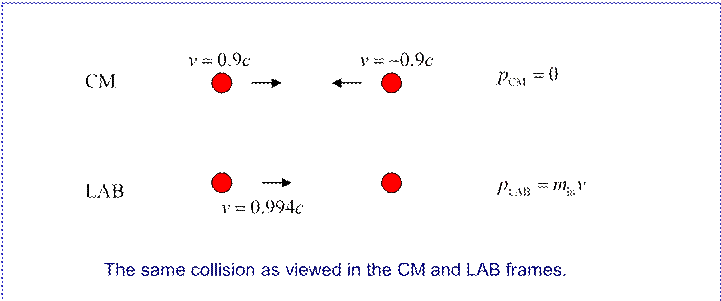
Comparing the center of mass energy with the lab energy at these high energies,

$\begin{matrix} E_{LAB} = (m_{in} + m_{0}) c^{2}, \\ E_{CM}^{2} = E_{LAB}^{2} - p_{LAB}^{2} c^{2} \\ = m_{in}^{2} c^{4} + 2 m_{in} c^{2} m_{0} c^{2} + m_{0}^{2} c^{4} - p_{LAB}^{2} c^{2} \\ = 2 m_{0} c^{2} (m_{in} c^{2} + m_{0} c^{2}) . \end{matrix}$

For $m ≫ m_{0},$

$E_{C M}^{2} \approx 2 m_{0} c^{2} m c^{2} \approx 2 m_{0} c^{2} . E_{L A B}$

$E_{C M} \approx \sqrt{2 m_{0} c^{2} . E_{L A B}}$ ,

ultimately one must quadruple the lab energy to double the center of mass energy. And, at higher energies, things get steadily worse——his is why colliders were built!

previous home next