previous  home  next

Time Dilation: A Worked Example

Michael Fowler, University of Virginia

“Moving Clocks Run Slow” plus “Moving Clocks Lose Synchronization” plus “Length Contraction” leads to consistency!

The object of this exercise is to show explicitly how it is possible for two observers in inertial frames moving relative to each other at a relativistic speed to each see the other’s clocks as running slow and as being unsynchronized, and yet if they both look at the same clock at the same time from the same place (which may be far from the clock), they will agree on what time it shows!

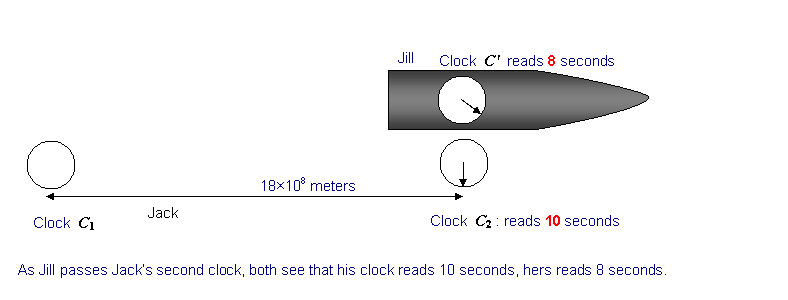
Suppose that in Jack’s frame we have two synchronized clocks C₁ and C₂ set 18 x 10⁸ meters apart (that’s about a million miles, or 6 light-seconds).  Jill’s spaceship, carrying a clock C',  is traveling at 0.6c, that is 1.8 x 10⁸ meters per second, parallel to the line C₁C₂, passing close by each clock.

Suppose C'  is synchronized with C₁ as they pass, so both read zero.

As measured by Jack the spaceship will take just 10 seconds to reach C₂, since the distance is 6 light seconds, and the ship is traveling at 0.6c. 

What does clock C' (the clock on the ship) read as it passes C₂?

The time dilation factor

1− v 2 / c 2 =4/5, 

 so C', Jill’s clock, will read 8 seconds.

Thus if both Jack and Jill are at C₂ as Jill and her clock C'  pass C₂ , both will agree that the clocks look like:

How, then, can Jill  claim that Jack’s clocks C₁, C₂ are the ones that are running slow?

To Jill, C₁, C₂ are running slow, but remember they are not synchronized.

To Jill, C₁ is behind  C₂  by Lv/ c 2 =( L/c )⋅( v/c )=6⋅0.6=3.6 seconds. 

Therefore, Jill will conclude that since C₂ reads 10 seconds as she passes it, at that instant C₁ must be registering 6.4 seconds.  Jill’s own clock reads 8 seconds at that instant, so she concludes that C₁ is running slow by the appropriate time dilation factor of 4/5. 

This is how the change in synchronization makes it possible for both Jack and Jill to see the other’s clocks as running slow.

Of course, Jill’s assertion that as she passes Jack’s second “ground” clock C₂ the first “ground” clock C₁ must be registering 6.4 seconds is not completely trivial to check!  After all, that clock is now a million miles away!

Let us imagine, though, that both observers are equipped with Hubble-style telescopes, so reading a clock a million miles away is no trick.

To settle the argument, the two of them agree that as she passes the second clock, Jack will be stationed at the second clock, and at the instant of her passing they will both photograph the faraway clock C₁, to see what time it reads.

Jack, of course, knows that C₁ is 6 light seconds away, and is synchronized with C₂ which at that instant is reading 10 seconds, so his snapshot must show C₁ to read 4 seconds.  That is, looking at C₁ he sees it as it was six seconds ago.

What does Jill’s digital snapshot show?  It must be identical—two snapshots taken from the same place at the same time must show the same thing!  So, Jill must also gets a picture of C₁ reading 4 seconds.

How can she reconcile a picture of the clock reading 4 seconds with her assertion that at the instant she took the photograph the clock was registering 6.4 seconds?

The answer is that she can if she knows her relativity!

First point: length contraction. To Jill, the clock C₁ is actually only 4/5 x 18 x 10⁸ meters away (she sees the distance C₁C₂ to be Lorentz contracted!).

Second point: The light didn’t even have to go that far!  In her frame, the clock C₁ is moving away, so the light arriving when she’s at C₂ must have left C₁ when it was closer—at distance x in the figure below. The figure shows the light in her frame moving from the clock towards her at speed c, while at the same time the clock itself is moving to the left at 0.6c.  

It might be helpful to imagine yourself in her frame of reference, so you are at rest, and to think of clocks C₁ and C₂ as being at the front end and back end respectively of a train that is going past you at speed 0.6c, Then, at the moment the back of the train passes you, you take a picture (through your telescope, of course) of the clock at the front of the train.  Obviously, the light from the front clock that enters your camera at that instant left the front clock some time ago.  During the time that light traveled towards you at speed c, the front of the train itself was going in the opposite direction at speed 0.6c.  But you know the length of the train in your frame is 4/5 x 18 x 10⁸ meters, so since at the instant you take the picture the back of the train is passing you, the front of the train must be 4/5 x 18 x 10⁸ meters away. Now that distance, 4/5 x 18 x 10⁸, is the sum of the distance the light entering your camera traveled plus the distance the train traveled in the same time, that is, (1 + 0.6)/1 times the distance the light traveled.

So the image of the first ground clock she sees and records as she passes the second ground clock must have been emitted when the first clock was a distance x from her in her frame, where

x( 1+3/5 )=4/5×18× 10 8 meters, so x=9× 10 8 meters.

Having established that the clock image she is seeing as she takes the photograph left the clock when it was only 9 x 10⁸ meters away, that is, 3 light seconds, she concludes that she is observing the first ground clock as it was three seconds ago.

Third point: time dilation. The story so far: she has a photograph of the first ground clock that shows it to be reading 4 seconds. She knows that the light took three seconds to reach her.  So, what can she conclude the clock must actually be registering at the instant the photo was taken?  If you are tempted to say 7 seconds, you have forgotten that in her frame, the clock is moving at 0.6c and hence runs slow by a factor 4/5.

Including the time dilation factor correctly, she concludes that in the 3 seconds that the light from the clock took to reach her, the clock itself will have ticked away 3 × 4/5 seconds, or 2.4 seconds.

Therefore, since the photograph shows the clock to read 4 seconds, and she finds the clock must have run a further 2.4 seconds, she deduces that at the instant she took the photograph the clock must actually have been registering 6.4 seconds, which is what she had claimed all along!

The key point of this lecture is that at first it seems impossible for two observers moving relative to each other to both maintain that the other one’s clocks run slow.  However, by bringing in the other necessary consequences of the theory of relativity, the Lorentz contraction of lengths, and that clocks synchronized in one frame are out of synchronization in another by a precise amount that follows necessarily from the constancy of the speed of light, the whole picture becomes completely consistent!

previous  home  next