Chapter 6

Mechanical Properties of Solids

We now turn to discuss the properties of solids, especially of monatomic solids, alloys, and simple compounds. Many materials of technological interest fall in these categories, but wood for instance does not. Rocks in the earth's crust often consist of aggregates of very small crystals that are themselves fairly simple; commonly, they have variable composition. The study of solids goes under various names: crystallography, solid state physics, and materials science. There are also the related fields of solid state chemistry, mineralogy, surface science, and others. These names reflect the different backgrounds and interests of workers in this vast area. Human technology has relied heavily on solids from the stone age, to the iron age, to the transistor age.

We can broadly divide the subject into two parts: mechanical properties and transport properties (electrical and thermal conduction). We start with mechanical properties such as such as stiffness, strength, and toughness, which we will define as we go along. For specific applications, we would like to engineer or design materials with the appropriate combination of these qualities.

6.1 Stiffness

How "stiff" or "flexible" is a material? It depends on whether we pull on it, twist it, bend it, or simply compress it. We shall see that in the simplest case the material is characterized by two independent "stiffness constants" and that different combinations of these constants determine the response to a pull, twist, bend, or pressure. This simplest behavior occurs when the material deforms elastically, or more precisely within the bounds of linear elasticity, and further it is effectively homogeneous and elastically isotropic. A material behaves elastically if it returns to its original shape when the stress is removed; linear elastic behavior is an idealization that is quite accurate for small deformations (typically less than 1%). A piece of an amorphous solid or a glass of constant composition is homogeneous and isotropic in all its properties, on a scale larger than atomic size. On the other hand, a piece of wood is not isotropic in many of its properties, including elasticity, and is not homogeneous on a small enough scale ( it has a "grain"), but is effectively homogeneous for deformations on a scale larger than the grain. Single crystals are not elastically isotropic (and are anisotropic in other ways too: for instance, they show preferred faceting). Rocks and metals often consist of many microcrystals and are elastically isotropic for deformations on a scale larger than the microcrystals. This is true despite the fact that the microcrystals themselves are elastically anisotropic, provided they are randomly oriented. Since the microcrystal size can be as small as 0.1mm, it is hard to distinguish a finely microcrystalline material from an amorphous one.

If a material is anisotropic, we must repeat the arguments given below for pulls (or bends) in different directions, and the question will be how many independent such pulls must be considered, or how many independent elastic constants characterize the material. If a material is inhomogeneous, we can think of it as consisting of homogeneous little pieces, infinitely many of them if the composition varies continuously.

6.1.1 Stress and strain

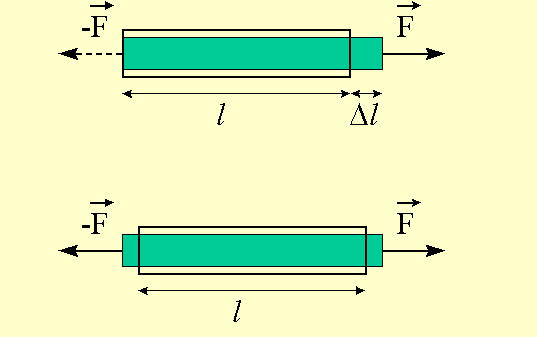
Pull on a bar of length l with a force F : it will elongate by an amount Dl (see figure 6.1). The stress which is applied at the ends of the bar is F/A, where A is the cross-sectional area of the bar. Stress has the same dimensions as pressure (its SI units are pascals, with 1 psi = 6891 Pa), but conventionally a positive stress (pulling out) corresponds to a negative pressure.

The deformation of the bar is described by dimensionless ratios called strains. An obvious strain is the fractional elongation Dl/l, which is positive for a bar in tension, negative for a bar in compression.
Hooke's law, valid for small strains, tells us that the fractional elongation is proportional to the stress:

Dl/l = E F/A

where E is the Young modulus (also denoted by Y). The dimensions of E are the same as those of stress and pressure.

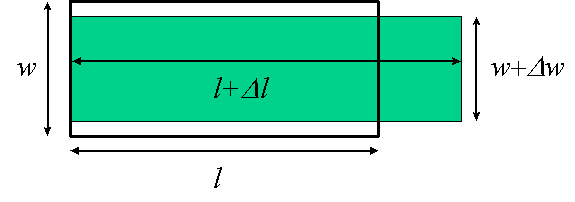
The bar also gets thinner in the directions perpendicular to the force: as shown in Fig. 5.2 a transverse dimension w is reduced to w+Dw (with Dw < 0). The fractional shrinkage Dw/w is also a strain; if small, it is proportional to the stress F/A, and thus proportional to Dl/l. The Poisson ratio n (also called s) is defined by

Dw/w = -n Dl/l

and can have any value between 0 and ½. The reason for the upper limit on n is that the volume change DV must be positive, and one can show that DV/V = (1 - 2n)Dl/l.

: