Physics 311 - Fall 97
Problem set 8
Due Thursday, Nov 13
- 1.
- Compression waves in a thin elastic bar. An elastic bar made of
a material with a Young's modulus E and a density
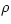 has a
cross-sectional area A. In this problem you will derive the wave equation
for compression waves in the bar.
has a
cross-sectional area A. In this problem you will derive the wave equation
for compression waves in the bar.
- (a)
- Let the displacement of an element of the bar from its equilibrium
position be u(x), where x labels the position along the bar. Show that
in this situation the stress s(x) at a point x is
| 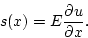 |
(1) |
- (b)
- Now consider a small segment of the bar of length
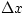 . There
is a force F(x) acting on the left end of this piece and a force
. There
is a force F(x) acting on the left end of this piece and a force 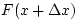 acting on the right end. Show that the net force acting on
this segment is
acting on the right end. Show that the net force acting on
this segment is
| 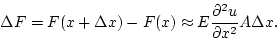 |
(2) |
- (c)
- Now apply Newton's Second Law to this segment and show that the
displacement satisfies the wave equation; i.e.,
| 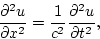 |
(3) |
where the wave speed is 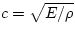 .
. - (d)
- As the wave travels down the bar, what happens to the diameter of the
bar?
- 2.
- Wave speeds. Look up the Young's modulus, shear modulus, and
Poisson's ratio for three different materials (your choice). Calculate the
speed of torsional and compressional waves in these materials. Any
conclusions?
- 3.
- Dislocations.
- (a)
- On page 30-16 of Feynman, volume II, are three pictures of
bubble rafts. Make a photocopy and mark the positions of the dislocations.
Find their Burgers vectors.
- (b)
- Take a few paragraphs to explain why the existence and motion of
dislocations explains the strength (i.e., the yield stress) of ductile
materials. Why are alloys usually harder than pure metals?
- 4.
- Bursting pressure. Here we will calculate the bursting
pressure of a steel container. Assume that the container is a cylinder of
length L, radius R, with wall thickness t (
 ); the pressure of
the gas inside the tank relative to the outside pressure is
); the pressure of
the gas inside the tank relative to the outside pressure is 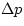 .
.
- (a)
- By considering a small portion of the wall of the tank, calculate the
stress s in the wall in terms of t, R, and
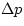 (and anything
else which might be important). The tank will burst when this stress exceeds
the yield stress
(and anything
else which might be important). The tank will burst when this stress exceeds
the yield stress  of the tank walls. Use this fact to
calculate the bursting pressure of the tank.
of the tank walls. Use this fact to
calculate the bursting pressure of the tank.
- (b)
- A scuba tank has typical dimensions L = 24", R = 5", t = 1/4". By
using a typical value of the yield stress for steel (see PQRG),
calculate the bursting pressure for this tank.
- (c)
- Now you probably don't want to fill the tank to the bursting
pressure--the actual bursting pressure may be lower than the theoretical
value for any number of reasons (what might they be?). So assume that the
tank is pressurized with air to 1/2 the theoretical bursting pressure. How
long a dive could you make with such a tank?
V. Celli, Univ. of Virginia
11/7/1997
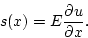
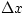 . There
is a force F(x) acting on the left end of this piece and a force
. There
is a force F(x) acting on the left end of this piece and a force 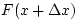 acting on the right end. Show that the net force acting on
this segment is
acting on the right end. Show that the net force acting on
this segment is
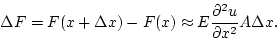
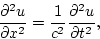
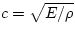 .
.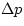 (and anything
else which might be important). The tank will burst when this stress exceeds
the yield stress
(and anything
else which might be important). The tank will burst when this stress exceeds
the yield stress  of the tank walls. Use this fact to
calculate the bursting pressure of the tank.
of the tank walls. Use this fact to
calculate the bursting pressure of the tank.