Review complex numbers, especially Euler's formula 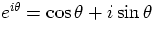 ;
the real and imaginary parts of a complex number, as in
z = x+iy, with x = Re z and y =
Im z; the modulus (magnitude) and phase of a complex number, as in
;
the real and imaginary parts of a complex number, as in
z = x+iy, with x = Re z and y =
Im z; the modulus (magnitude) and phase of a complex number, as in
 , with
, with

the notion of complex conjugate 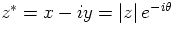 ;the product of complex numbers and in particular
;the product of complex numbers and in particular 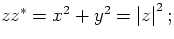 and the inverse of a complex number, as in
and the inverse of a complex number, as in
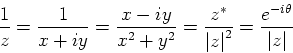
These formulas are very convenient to find current-
voltage relations in a circuit (or part of it), with 
 and impedance
and impedance
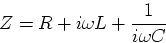
(Note: in discussing the harmonic oscillator, we used  for
consistency with quantum theory, because in quantum theory the time
evolution of an eigenstate is given by
for
consistency with quantum theory, because in quantum theory the time
evolution of an eigenstate is given by  , with
, with 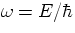 . However, in circuit theory it is customary to use
. However, in circuit theory it is customary to use  , and here we follow this convention, as in Feynman, Chapter 22,
volume II. Tipler uses phasors rotating counterclockwise, which are
equivalent to using
, and here we follow this convention, as in Feynman, Chapter 22,
volume II. Tipler uses phasors rotating counterclockwise, which are
equivalent to using  .)
.)
All the formulas developed for d.c. circuits can be directly extended to
a.c. circuits. Simply, V = ZI and
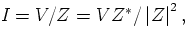 with
with
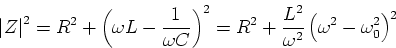
where  is the resonant frequency of the circuit. Also,
in the end we are usually interested in time-averaged values, which can be
computed as shown below for the dissipated power. Use this to solve problems
2 and 3 in Assignment 8.
is the resonant frequency of the circuit. Also,
in the end we are usually interested in time-averaged values, which can be
computed as shown below for the dissipated power. Use this to solve problems
2 and 3 in Assignment 8.
The time average of the dissipated power is
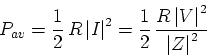
Defining Vrms by 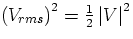 and Irms by
and Irms by 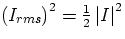 , we can also write
, we can also write
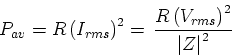
(Note: Tipler's Z is the modulus of the complex impedance, given by 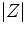 in our notation here.)
in our notation here.)
To obtain the formula for Pav, recall that the real potential and
current are obtained by taking the real part of V and I according to the
general formula Re z = 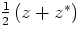 .
The instantaneous power is then 1/4 of
.
The instantaneous power is then 1/4 of
(I+I*)(V+V*) =
(I+I*)(ZI+Z*I*) =
ZI2 + Z*I* 2 + (Z+Z*)II*.
The average of 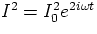 is 0, and so is the average of
I*2, while Z+Z*=2R.
is 0, and so is the average of
I*2, while Z+Z*=2R.
Vittorio Celli
3/29/1999
![]()
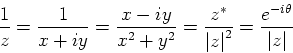
![]()
![]() and impedance
and impedance
![]()
![]() with
with
![]()
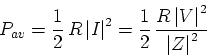
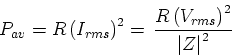
![]() .
The instantaneous power is then 1/4 of
.
The instantaneous power is then 1/4 of
![]() is 0, and so is the average of
I*2, while Z+Z*=2R.
is 0, and so is the average of
I*2, while Z+Z*=2R.