A/B = (B–A)/A
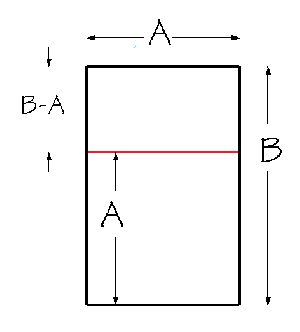
What is the ratio A/B for which this is true?
- f(x) = –xe–x×sinh2(x)/[1+cosh2(x)]
- f(x) = x4+x3+8x+8
f(x,y) = r–3 – r–1+r+x
where
r2=x2+y2 .
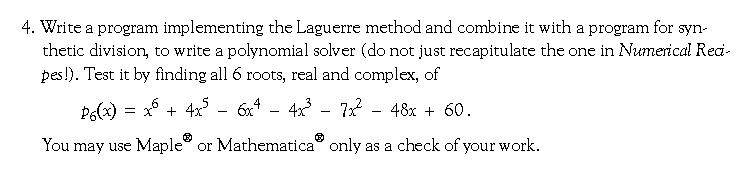


where
r2=x2+y2 .
SUBROUTINE TRIDAG(A,B,C,R,U,N)
PARAMETER (NMAX=100)
DIMENSION GAM(NMAX),A(N),B(N),C(N),R(N),U(N)
IF(B(1).EQ.0.)PAUSE
BET=B(1)
U(1)=R(1)/BET
DO 11 J=2,N
GAM(J)=C(J-1)/BET
BET=B(J)-A(J)*GAM(J)
IF(BET.EQ.0.)PAUSE
U(J)=(R(J)-A(J)*U(J-1))/BET
11 CONTINUE
DO 12 J=N-1,1,-1
U(J)=U(J)-GAM(J+1)*U(J+1)
12 CONTINUE
RETURN
END
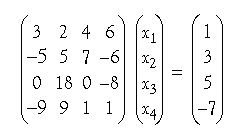
to 6 significant figures of precision. If you wish you may use Maple® or Mathematica® or Matlab® to check your work—or else multiply the matrix by the solution and see whether you obtain the inhomogeneous term.
 Assignment 4—due 26 November, 2001.
Assignment 4—due 26 November, 2001.