 or
or 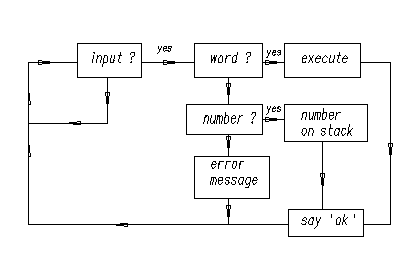 We might also have said
HEX 0A 14 * . <cr> C8 ok
(Do you understand this? Hint: DECIMAL means “switch to decimal arith-
metic”, whereas HEX stands for “switch to hexadecimal arithmetic”.)
If the incoming text can neither be located in the dictionary nor in-
terpreted as a number, Forth issues an error message. Try it: type X <cr>
and see
X
Error: X is undefined
or type THING <cr> and see
THING
Error: THING is undefined
Finally, here is the obligatory "Hello, World!" program. Forth lets you
output text using the word ." as follows (we will explain in §4 below
what : and ; mean):
: hi ." Hello, World!" ; ok
Now type in hi and see what happens:
hi Hello, World! ok
This can be elaborated with words that tab, emit carriage returns,
display in colors, etc. but that would take us too far afield.
(The word ." means “Display the string, following the obligatory blank space
and terminated by the close-quote " on the standard output device.”)
Forth belongs to the class of Threaded Interpretive Languages. This
means it can interpret commands (subroutines or programs) typed in
at the console, as well as create (compile) new subroutines and pro-
grams. The compiler in a traditional language has the structure shown
below:
We might also have said
HEX 0A 14 * . <cr> C8 ok
(Do you understand this? Hint: DECIMAL means “switch to decimal arith-
metic”, whereas HEX stands for “switch to hexadecimal arithmetic”.)
If the incoming text can neither be located in the dictionary nor in-
terpreted as a number, Forth issues an error message. Try it: type X <cr>
and see
X
Error: X is undefined
or type THING <cr> and see
THING
Error: THING is undefined
Finally, here is the obligatory "Hello, World!" program. Forth lets you
output text using the word ." as follows (we will explain in §4 below
what : and ; mean):
: hi ." Hello, World!" ; ok
Now type in hi and see what happens:
hi Hello, World! ok
This can be elaborated with words that tab, emit carriage returns,
display in colors, etc. but that would take us too far afield.
(The word ." means “Display the string, following the obligatory blank space
and terminated by the close-quote " on the standard output device.”)
Forth belongs to the class of Threaded Interpretive Languages. This
means it can interpret commands (subroutines or programs) typed in
at the console, as well as create (compile) new subroutines and pro-
grams. The compiler in a traditional language has the structure shown
below:
 To compile and test a program in a traditional language such
as Fortran, C or Pascal, one prepares an input (source) file, submits it
to a black box that someone else created (the compiler) and then
runs the resulting executable file (which is generally in machine
language). This process can be so tedious that most program
development in traditional languages must be supported by
an elaborate set of programs called the “environment”,
consisting of integrated editors, debuggers, version control
catalogues and the like.
The outer interpreter/compiler of a Forth system looks like this:
To compile and test a program in a traditional language such
as Fortran, C or Pascal, one prepares an input (source) file, submits it
to a black box that someone else created (the compiler) and then
runs the resulting executable file (which is generally in machine
language). This process can be so tedious that most program
development in traditional languages must be supported by
an elaborate set of programs called the “environment”,
consisting of integrated editors, debuggers, version control
catalogues and the like.
The outer interpreter/compiler of a Forth system looks like this:
 Forth has little in common with the traditional compilation method.
Although the Forth interpreter/compiler diagrammed above looks
complicated, it is simplicity itself compared with the contents of
the
Forth has little in common with the traditional compilation method.
Although the Forth interpreter/compiler diagrammed above looks
complicated, it is simplicity itself compared with the contents of
the  representing a traditional black-box compiler.
A continuous loop waits for input—from the keyboard, a disk file or
whatever— and acts on it according to its nature. Input consists
of a sequence of words and numbers. If a name is recognized it is
executed; if it is not in the dictionary (where else would you keep
a list of words?) Forth tries to convert it to a number and push it
on the stack. If this is impossible, Forth aborts execution, issues an
error message and waits for more input.
As we shall see below, what makes Forth a compiler as well as an
interpreter is the set of words (Forth subroutines) that, when they are
typed in and executed, create new Forth subroutines.
4. Extending the dictionary
The compiler is one of Forth's most endearing features. Unlike
most other high-level languages, the Forth compiler is part of the
language. (LISP and its dialects also make components of the com-
pilation mechanism available to the programmer.) That is, its com-
ponents are Forth words available to the programmer, that can be
used to solve his problems.
In this section we discuss how the compiler extends the
dictionary. As noted above, normally a Forth system awaits
input, and interprets (and executes it). We say the system is
normally in interpret mode.
Forth uses special words to create new dictionary entries, i.e.,
new words. The most important are ":" (“start a new definition”)
and ";" (“terminate the definition”).
Let's try this out: enter
: *+ * + ; <cr> ok
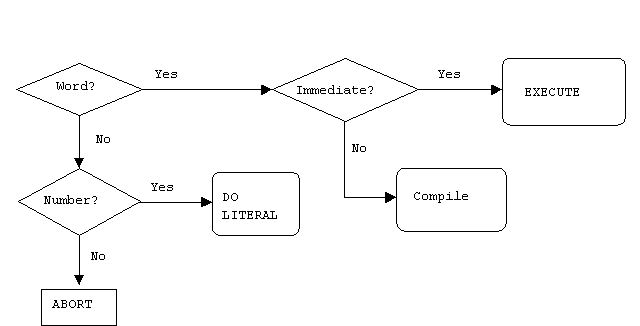
What happened? The word ":" was executed because it was already
in the dictionary. The action of ":" is
> Create a new dictionary entry named *+ and switch from
interpret to compile mode.
> In compile mode, the interpreter looks up words and
—rather than executing them— installs pointers to
their code. (If the text is a number, instead of
pushing it on the stack, Forth builds the number
into the dictionary space allotted for the new word,
following special code that puts the stored number
on the stack whenever that word is executed.)
> The action of "*+" is thus to execute sequentially
the previously-defined words "*" and "+".
> The word ";" is special: when it was defined a bit
was turned on in its dictionary entry to mark it as
IMMEDIATE. Thus, rather than writing down the address
of ";", the compiler executes ";" immediately.
(That is, an IMMEDIATE word is always executed, even
if the system is in compile mode.)
What ";" does is twofold: first, it installs the code
that returns control to the next outer level of the
interpreter; and second, it switches back from compile
mode to interpret mode.
Now try out *+ :
DECIMAL 5 6 7 *+ . <cr> 47 ok
This example illustrated two principles of Forth: adding a new word to
the dictionary, and trying it out as soon as it was defined.
The diagram below is a flow chart representing the actions performed
by the Forth inner interpreter during compilation.
representing a traditional black-box compiler.
A continuous loop waits for input—from the keyboard, a disk file or
whatever— and acts on it according to its nature. Input consists
of a sequence of words and numbers. If a name is recognized it is
executed; if it is not in the dictionary (where else would you keep
a list of words?) Forth tries to convert it to a number and push it
on the stack. If this is impossible, Forth aborts execution, issues an
error message and waits for more input.
As we shall see below, what makes Forth a compiler as well as an
interpreter is the set of words (Forth subroutines) that, when they are
typed in and executed, create new Forth subroutines.
4. Extending the dictionary
The compiler is one of Forth's most endearing features. Unlike
most other high-level languages, the Forth compiler is part of the
language. (LISP and its dialects also make components of the com-
pilation mechanism available to the programmer.) That is, its com-
ponents are Forth words available to the programmer, that can be
used to solve his problems.
In this section we discuss how the compiler extends the
dictionary. As noted above, normally a Forth system awaits
input, and interprets (and executes it). We say the system is
normally in interpret mode.
Forth uses special words to create new dictionary entries, i.e.,
new words. The most important are ":" (“start a new definition”)
and ";" (“terminate the definition”).
Let's try this out: enter
: *+ * + ; <cr> ok
What happened? The word ":" was executed because it was already
in the dictionary. The action of ":" is
> Create a new dictionary entry named *+ and switch from
interpret to compile mode.
> In compile mode, the interpreter looks up words and
—rather than executing them— installs pointers to
their code. (If the text is a number, instead of
pushing it on the stack, Forth builds the number
into the dictionary space allotted for the new word,
following special code that puts the stored number
on the stack whenever that word is executed.)
> The action of "*+" is thus to execute sequentially
the previously-defined words "*" and "+".
> The word ";" is special: when it was defined a bit
was turned on in its dictionary entry to mark it as
IMMEDIATE. Thus, rather than writing down the address
of ";", the compiler executes ";" immediately.
(That is, an IMMEDIATE word is always executed, even
if the system is in compile mode.)
What ";" does is twofold: first, it installs the code
that returns control to the next outer level of the
interpreter; and second, it switches back from compile
mode to interpret mode.
Now try out *+ :
DECIMAL 5 6 7 *+ . <cr> 47 ok
This example illustrated two principles of Forth: adding a new word to
the dictionary, and trying it out as soon as it was defined.
The diagram below is a flow chart representing the actions performed
by the Forth inner interpreter during compilation.
 Any word you have added to the dictionary can be decompiled using
the Forth word SEE. Say
SEE *+ <cr>
and get
SEE *+
: *+ * + ; ok
This can be useful when trying to understand how something works.
5. Stacks and reverse Polish notation (RPN)
We now discuss the stack and the “reverse Polish” or “postfix” arith-
metic based on it. (Anyone who has used a Hewlett-Packard calculator
should be familiar with the concept.)
Virtually all modern CPU's are designed around stacks. Forth effi-
ciently uses its CPU by reflecting this underlying stack architecture
in its syntax.
But what is a stack? As the name implies, a stack is the machine ana-
log of a pile of cards with numbers written on them. Numbers are
always added to the top of the pile, and removed from the top of the
pile. The Forth input line
2 5 73 -16 <cr> ok
leaves the stack in the state
cell # contents
0 -16 (TOS)
1 73 (NOS)
2 5
3 2
where TOS stands for “top-of-stack”, NOS for “next-on-stack”, etc.
We usually employ zero-based relative numbering in Forth data struct-
ures (such as stacks, arrays, tables, etc.) so TOS is given relative
#0, NOS #1, etc.
Suppose we followed the above input line with the line
+ - * . <cr> xxx ok
what would xxx be? The operations would produce the successive stacks
cell# initial + - * .
stack
0 -16 57 -52 -104
1 73 5 2
2 5 2
3 2 empty ( 104 -> CRT )
stack
The operation "." (TOS->display) displays -104 to the screen, leaving the
stack empty. That is, xxx is -104.
a. Manipulating the parameter stack
Forth systems incorporate (at least) two stacks: the parameter stack
and the return stack.
A stack-based system must provide ways to put numbers on the stack, to
remove them, and to rearrange their order. Forth includes standard
words for this purpose.
Putting numbers on the stack is easy: simply type the number (or in-
corporate it in the definition of a Forth word).
The word DROP removes the number from TOS and moves up all the other
numbers. (Since the stack usually grows downward in memory, DROP mere-
ly increments the pointer to TOS by 1 cell.)
SWAP exchanges the top 2 numbers.
DUP duplicates the TOS into NOS.
ROT rotates the top 3 numbers.
These actions are shown below (we show what each word does to the ini-
tial stack)
cell | initial | DROP SWAP ROT DUP
0 | -16 | 73 73 5 -16
1 | 73 | 5 -16 -16 -16
2 | 5 | 2 5 73 73
3 | 2 | 2 2 5
4 | | 2
Forth includes the words OVER, TUCK, PICK and ROLL that act as shown
below (note PICK and ROLL must be preceded by an integer that says
where on the stack an element gets PICK'ed or ROLL'ed):
cell | initial | OVER TUCK 3 PICK 3 ROLL
0 | -16 | 73 -16 2 2
1 | 73 | -16 73 -16 -16
2 | 5 | 73 -16 73 73
3 | 2 | 5 5 5 5
4 | | 2 2 2
Clearly, 0 PICK is the same as DUP, 1 PICK is a synonym for OVER, 1 ROLL
means SWAP and 2 ROLL means ROT.
The words PICK and ROLL are mainly useful for dealing with deep stacks. But
the current trend in Forth programming is to avoid making the stack deeper
than 3 or 4 elements. A deeper stack than that is generally considered a sign
that the program has been insufficiently thought out and needs to be factored.
b. Remarks on factoring
Factoring is the process of breaking out repeated pieces of code from sub-
routines and giving them a name. This not only shortens the overall program
but can make the code simpler. Here is a frequently offereded illustration:
: SUM-OF-SQUARES ( a b -- a*a+b*b ) DUP * SWAP DUP * + ;
has the repeated phrase DUP * and can be replaced profitably by
: SQUARED ( a -- a*a ) DUP * ;
: SUM-OF-SQUARES ( a b -- a*a+b*b )
SQUARED ( -- a b*b)
SWAP ( -- b*b a)
SQUARED ( -- b*b a*a)
+ ( -- b*b + a*a)
;
The new version of SUM-OF-SQUARES is 2 words shorter and thus easier to read.
Before leaving this subject I would like to offer some deeper examples of factoring,
plus a badly factored definition. To begin with the badly factored word, look at
the file float.f in the Win32Forth main directory, and in particular at the word >float.
This word is almost 3 pages long, which makes it virtually impossible to read or
to maintain.
Here is an example of where factoring leads to great simplification. My linear equations
solver uses Gaussian elimination with row-pivoting. By appropriate transformations the
equations are put in the form of equations with an upper-triangular matrix. Once this is
done the equations can be solved for xk beginning with the n'th (which only requires a
single division to determine the unknown xn); the n-1'st can then be solved by equally
simple algebra in terms of xn, etc. This procedure is called “back-solving” because it
proceeds in reverse order. The word that does the all the work expects addresses of matrix
and inhomogeneous term on the data stack:
: }}solve ( A{{ V{ --)
initialize triangularize back-solve report ;
You will note that the words initialize, triangularize, back-solve and report were
given names that tell you precisely what they do. They represent the major steps of
the algorithm as described above. Of course they have to be defined before they
can be invoked. This is why we describe the typical Forth programming style as
“bottom-up” rather than “top-down” as with other languages.
My final example of factoring is a routine for adaptive numerical quadrature (integrating
a function of one variable) based on Simpson's Rule. To use it one says
use( fn.name xa xb err )integral
The algorithm computes the integral on an interval, then breaks it into two
equal sub-intervals. The sub-integrals are compared with the original—if
they agree within the tolerance the result is accumulated and the integral is
evaluated on the remainder of the interval. If they don't agree the routine
works on the upper sub-interval until convergence is achieved.
: )integral ( f: xa xb err -- I[xa,xb]) ( xt --)
initialize
BEGIN \ begin indefinite loop
subdivide \ break last subinterval in two
converged?
IF interpolate \ apply Richardson interpolation
shrink-interval
THEN
none-left UNTIL \ loop until done
TotIntegral F@ ( f: -- Integral) \ leave result
;
This version has been reduced to seven basic operations, not counting the
system words BEGIN, UNTIL that set up the loop; IF...THEN that sets
up the branch, and F@ that puts the answer on the stack.
c. The return stack and its uses
We have remarked above that compilation establishes links from the
calling word to the previously-defined word being invoked. The linkage
mechanism --during execution-- uses the return stack (rstack): the
address of the next word to be invoked is placed on the rstack, so
that when the current word is done executing, the system knows to jump
to the next word. (This is so in most, but not all, modern Forth imple-
mentations. But all have a return stack, whether or not they use them
for linking subroutines.)
In addition to serving as a reservoir of return addresses (since words
can be nested, the return addresses need a stack to be put on) the
rstack is where the limits of a DO...LOOP construct are placed.
The user can also store/retrieve to/from the rstack. This is an ex-
ample of using a component for a purpose other than the one it was
designed for. Such use is discouraged for novices since it adds the
spice of danger to programming. See “Note of caution” below.
To store to the rstack we say >R , and to retrieve we say R> . The
word R@ copies the top of the rstack to the TOS.
Why use the rstack when we have a perfectly good parameter stack to
play with? Sometimes it becomes hard to read code that performs com-
plex gymnastics on the stack. The rstack can reduce the complexity.
Alternatively, VARIABLEs —named locations— provide a place to store
numbers —such as intermediate results in a calculation— off the
stack, again reducing the gymnastics. Try this:
\ YOU DO THIS \ EXPLANATION
VARIABLE X <cr> ok \ create a named storage location X;
\ X executes by leaving its address
3 X ! <cr> ok \ ! ("store") expects a number and
\ an address, and stores the number to
\ that address
X @ . <cr> 3 ok \ @ ("fetch") expects an address, and
\ places its contents in TOS.
However, Forth encourages using as few named variables as possible.
The reason: since VARIABLEs are typically global —any subroutine can
access them— they can cause unwanted interactions among parts of a
large program.
Although Forth can make variables local to the subroutines that use
them (see “headerless words” in FTR), the rstack can often replace
local variables:
> The rstack already exists, so it need not be defined anew.
> When the numbers placed on it are removed, the rstack shrinks,
reclaiming some memory.
A note of caution: since the rstack is critical to execution we mess
with it at our peril. If we use the rstack for temporary storage we
must restore it to its initial state. A word that places a number on
the rstack must remove it —using R> or RDROP (if it has been defined)
— before exiting that word. Since DO...LOOP also uses the rstack,
for each >R folowing DO there must be a corresponding R> or RDROP
preceding LOOP. Neglecting these precautions will probably crash
the system.
RDROP is not an ANS Forth word that can be assumed predefined on any system.
Since it is not Standard, some systems call it R>DROP (which also is not
Standard). Here is its definition if needed:
: RDROP ( or R>DROP) ( r: n -- ) R> DROP ;
d. Local variables and VALUEs
I mentioned VARIABLEs above—a VARIABLE is a subroutine whose action is to
return the address of a named, cell-sized memory location, as in
VARIABLE x
x . 247496 ok ( it doesn't have to be this address!)
-49 x !
x @ . -49 ok
A VALUE is a widely used hybrid of VARIABLE and CONSTANT (see below). We
define and initialize a VALUE as we would a CONSTANT:
13 VALUE thirteen ok
We invoke the new VALUE just as we would a CONSTANT:
thirteen . 13 ok
However, we can change a VALUE as though it were a VARIABLE:
47 TO thirteen ok
thirteen . 47 ok
Needless to say, the word TO also works within word definitions, replacing
the VALUE that follows it with whatever is currently in TOS. (Note that
it would be dangerous to follow TO with anything but a VALUE !!) VALUEs
are part of the ANS Forth CORE EXTENSION wordset (that is, the corresponding
code is not guaranteed to be loaded on minimal ANS-compliant systems).
This is a good time to mention that Forth does no type-checking (unless you add
it yourself). YOU must check that TO is followed by a VALUE and not something
else.
ANS Forth also includes a LOCALS EXTENSION wordset that implements named memory
locations local to a word definition. Locals are generally dynamic in nature (that
is, their memory is reclaimed upon exiting the word), although the Standard does
not insist on this. A commonly used syntax is LOCALS| a b c ... |, as in this
definition (from a line-drawing algorithm):
: v+ ( a b c d -- a+c b+d)
LOCALS| d c b a |
a c + b d + ;
2 3 4 5 v+ .S [2] 6 8 ok.. ( .S displays the stack without destroying it)
The important things to remember are
> the names a, b, c ... can be any Forth-acceptable strings;
> the local names have meaning only within a word definition;
> the locals are initialized from the stack as shown in v+ above,
and as in the next example:
: test-locals ( a b c -- )
LOCALS| c b a |
CR ." Normal order: " a . b . c .
CR ." Stack order: " c . b . a .
13 TO a 14 TO b 15 TO c \ how TO works
CR ." Changed: " a . b . c
; ok
3 4 5 test-locals
Normal order: 3 4 5
Stack order: 5 4 3
Changed: 13 14 15 ok
> the locals act like VALUEs, not like VARIABLEs, as the above
example makes clear;
> the LOCALS EXTENSION wordset requires LOCALS| ... | to accomodate
(at least) 8 local names.
> LOCALS| ... | is never necessary, nor does it necessarily shorten code, as
the example below makes clear (7 words as opposed to 6 + preamble):
: v+ ( a b c d -- a+c b+d) 2>R R> + SWAP R> + SWAP ;
What it does accomplish is to reduce stack juggling and clarify the code
in some cases.
6. Using memory
As we just saw, ordinary numbers are fetched from memory to
the stack by @ ("fetch"), and stored by ! (store).
@ expects an address on the stack and replaces that address by
its contents using, e.g., the phrase X @
! expects a number (NOS) and an address (TOS) to store it in, and
places the number in the memory location referred to by the address,
consuming both arguments in the process, as in the phrase 3 X !
Double length numbers can similarly be fetched and stored, by
D@ and D!, if the system has these words.
Positive numbers that represent characters can be placed in character
-sized cells of memory using C@ and C!. This is convenient for operations
with strings of text, for example screen and keyboard I/O.
Of course, one cannot put numbers in memory or retrieve them,
for that matter, without a means of allocating memory and of
assigning labels to the memory so allocated.
The Forth subroutines CREATE and ALLOT are the basic tools for
setting aside memory and attaching a convenient label to it. As
we shall see below, CREATE makes a new dictionary entry, as in
CREATE X
Here the new entry has the name X, but it could have been "Joe"
or anything else. The new name is a Forth subroutine that will
return the address of the next available space in memory. Thus
CREATE X ok
X . 247316 ok
HERE . 247316 ok
HERE is a subroutine that returns the address of the next available
space—we note that it is the same as the address of X because no
space has been ALLOTted. We can rectify this by saying
10 CELLS ALLOT ok
and checking with
HERE . 247356 ok
We see that the next available space is now marked as 40 bytes
further up in memory. (Each CELL is therefore 4 bytes or 32 bits
on this system.) In other words, the subroutine ALLOT increases
the pointer HERE by the number of address units you have told
it to allot. You could have said
40 ALLOT
instead of
10 CELLS ALLOT
but the latter is more portable because it frees you from having
to revise your code if you were to run it on a system with 64-bit
or 16-bit cells (both of which are in common use).
By executing the sequence
CREATE X 10 CELLS ALLOT
we have set aside enough room to hold 10 32-bit numbers--for example
a table or array--that can be referenced by naming it. If we want to
get at the 6th element of the array (the first element has index 0,
so the 6th has index 5) we would say
X 5 CELLS +
to compute its address. To see how this works, let us say
137 X 5 CELLS + ! ok
to store an integer into the 6th array location; then
X 5 CELLS + @ . 137 ok
retrieves and displays it.
Using the tools provided by CREATE and ALLOT we can devise
any sort of data structure we like. This is why Forth does
not provide a panoply of data structures, such as are to be
found in languages like C, Pascal or Fortran. It is too easy
in Forth to custom tailor any sort of data structure one
wishes. In the section on CREATE...DOES> below you will see
that Forth makes it easy to write subroutines ("constructors")
that create custom data structures--that can even include
code fragments that do useful things. For example, a CONSTANT
is a number you would not want to change during a program's
execution. So you do not want access to its memory location.
How then do you get the number when you need it? You package
the code for @ with the storage location, so that by naming
the CONSTANT you retrieve its contents. Its usage is
17 CONSTANT seventeen ok
seventeen . 17 ok
7. Comparing and branching
Forth lets you compare two numbers on the stack, using relational
operators ">", "<", "=" . Thus, e.g., the phrase
2 3 > <cr> ok
leaves 0 ("false") on the stack, because 2 (NOS) is not greater than 3
(TOS). Conversely, the phrase
2 3 < <cr> ok
leaves -1 ("true") because 2 is less than 3.
Notes: In some Forths “true” is +1 rather than -1.
Relational operators consume both arguments and leave a “flag”
to show what happened.
(Many Forths offer unary relational operators "0=", "0>" and "0<".
These, as might be guessed, determine whether the TOS contains an
integer that is 0, positive or negative.)
The relational words are used for branching and control. For example,
: TEST 0 = INVERT IF CR ." Not zero!" THEN ;
0 TEST <cr> ok ( no action)
-14 TEST <cr>
Not zero! ok
The TOS is compared with zero, and the INVERT operator (bitwise logical
NOT—this flips "true" and "false") is applied to the resulting flag. The
word CR issues a carriage return (newline). Finally, if TOS is non-zero,
IF swallows the flag and executes all the words between itself and the
terminating THEN. If TOS is zero, execution jumps to the word following
THEN.
The word ELSE is used in the IF...ELSE...THEN statement: a nonzero
value in TOS causes any words between IF and ELSE to be executed, and
words between ELSE and THEN to be skipped. A zero value produces the
opposite behavior. Thus, e.g.
: TRUTH CR 0 = IF ." false" ELSE ." true" THEN ;
1 TRUTH <cr>
true ok
0 TRUTH <cr>
false ok
Since THEN is used to terminate an IF statement rather than in its
usual sense, some Forth writers prefer the name ENDIF.
8. Documenting and commenting Forth code
Forth is sometimes accused of being a "write-only" language, i.e. some
complain that Forth is cryptic. This is really a complaint against
poor documentation and untelegraphic word names. Unreadability is
equally a flaw of poorly written FORTRAN, PASCAL, C, etc.
Forth offers programmers who take the trouble tools for producing ex-
ceptionally clear code.
a. Parenthesized remarks
The word (
Any word you have added to the dictionary can be decompiled using
the Forth word SEE. Say
SEE *+ <cr>
and get
SEE *+
: *+ * + ; ok
This can be useful when trying to understand how something works.
5. Stacks and reverse Polish notation (RPN)
We now discuss the stack and the “reverse Polish” or “postfix” arith-
metic based on it. (Anyone who has used a Hewlett-Packard calculator
should be familiar with the concept.)
Virtually all modern CPU's are designed around stacks. Forth effi-
ciently uses its CPU by reflecting this underlying stack architecture
in its syntax.
But what is a stack? As the name implies, a stack is the machine ana-
log of a pile of cards with numbers written on them. Numbers are
always added to the top of the pile, and removed from the top of the
pile. The Forth input line
2 5 73 -16 <cr> ok
leaves the stack in the state
cell # contents
0 -16 (TOS)
1 73 (NOS)
2 5
3 2
where TOS stands for “top-of-stack”, NOS for “next-on-stack”, etc.
We usually employ zero-based relative numbering in Forth data struct-
ures (such as stacks, arrays, tables, etc.) so TOS is given relative
#0, NOS #1, etc.
Suppose we followed the above input line with the line
+ - * . <cr> xxx ok
what would xxx be? The operations would produce the successive stacks
cell# initial + - * .
stack
0 -16 57 -52 -104
1 73 5 2
2 5 2
3 2 empty ( 104 -> CRT )
stack
The operation "." (TOS->display) displays -104 to the screen, leaving the
stack empty. That is, xxx is -104.
a. Manipulating the parameter stack
Forth systems incorporate (at least) two stacks: the parameter stack
and the return stack.
A stack-based system must provide ways to put numbers on the stack, to
remove them, and to rearrange their order. Forth includes standard
words for this purpose.
Putting numbers on the stack is easy: simply type the number (or in-
corporate it in the definition of a Forth word).
The word DROP removes the number from TOS and moves up all the other
numbers. (Since the stack usually grows downward in memory, DROP mere-
ly increments the pointer to TOS by 1 cell.)
SWAP exchanges the top 2 numbers.
DUP duplicates the TOS into NOS.
ROT rotates the top 3 numbers.
These actions are shown below (we show what each word does to the ini-
tial stack)
cell | initial | DROP SWAP ROT DUP
0 | -16 | 73 73 5 -16
1 | 73 | 5 -16 -16 -16
2 | 5 | 2 5 73 73
3 | 2 | 2 2 5
4 | | 2
Forth includes the words OVER, TUCK, PICK and ROLL that act as shown
below (note PICK and ROLL must be preceded by an integer that says
where on the stack an element gets PICK'ed or ROLL'ed):
cell | initial | OVER TUCK 3 PICK 3 ROLL
0 | -16 | 73 -16 2 2
1 | 73 | -16 73 -16 -16
2 | 5 | 73 -16 73 73
3 | 2 | 5 5 5 5
4 | | 2 2 2
Clearly, 0 PICK is the same as DUP, 1 PICK is a synonym for OVER, 1 ROLL
means SWAP and 2 ROLL means ROT.
The words PICK and ROLL are mainly useful for dealing with deep stacks. But
the current trend in Forth programming is to avoid making the stack deeper
than 3 or 4 elements. A deeper stack than that is generally considered a sign
that the program has been insufficiently thought out and needs to be factored.
b. Remarks on factoring
Factoring is the process of breaking out repeated pieces of code from sub-
routines and giving them a name. This not only shortens the overall program
but can make the code simpler. Here is a frequently offereded illustration:
: SUM-OF-SQUARES ( a b -- a*a+b*b ) DUP * SWAP DUP * + ;
has the repeated phrase DUP * and can be replaced profitably by
: SQUARED ( a -- a*a ) DUP * ;
: SUM-OF-SQUARES ( a b -- a*a+b*b )
SQUARED ( -- a b*b)
SWAP ( -- b*b a)
SQUARED ( -- b*b a*a)
+ ( -- b*b + a*a)
;
The new version of SUM-OF-SQUARES is 2 words shorter and thus easier to read.
Before leaving this subject I would like to offer some deeper examples of factoring,
plus a badly factored definition. To begin with the badly factored word, look at
the file float.f in the Win32Forth main directory, and in particular at the word >float.
This word is almost 3 pages long, which makes it virtually impossible to read or
to maintain.
Here is an example of where factoring leads to great simplification. My linear equations
solver uses Gaussian elimination with row-pivoting. By appropriate transformations the
equations are put in the form of equations with an upper-triangular matrix. Once this is
done the equations can be solved for xk beginning with the n'th (which only requires a
single division to determine the unknown xn); the n-1'st can then be solved by equally
simple algebra in terms of xn, etc. This procedure is called “back-solving” because it
proceeds in reverse order. The word that does the all the work expects addresses of matrix
and inhomogeneous term on the data stack:
: }}solve ( A{{ V{ --)
initialize triangularize back-solve report ;
You will note that the words initialize, triangularize, back-solve and report were
given names that tell you precisely what they do. They represent the major steps of
the algorithm as described above. Of course they have to be defined before they
can be invoked. This is why we describe the typical Forth programming style as
“bottom-up” rather than “top-down” as with other languages.
My final example of factoring is a routine for adaptive numerical quadrature (integrating
a function of one variable) based on Simpson's Rule. To use it one says
use( fn.name xa xb err )integral
The algorithm computes the integral on an interval, then breaks it into two
equal sub-intervals. The sub-integrals are compared with the original—if
they agree within the tolerance the result is accumulated and the integral is
evaluated on the remainder of the interval. If they don't agree the routine
works on the upper sub-interval until convergence is achieved.
: )integral ( f: xa xb err -- I[xa,xb]) ( xt --)
initialize
BEGIN \ begin indefinite loop
subdivide \ break last subinterval in two
converged?
IF interpolate \ apply Richardson interpolation
shrink-interval
THEN
none-left UNTIL \ loop until done
TotIntegral F@ ( f: -- Integral) \ leave result
;
This version has been reduced to seven basic operations, not counting the
system words BEGIN, UNTIL that set up the loop; IF...THEN that sets
up the branch, and F@ that puts the answer on the stack.
c. The return stack and its uses
We have remarked above that compilation establishes links from the
calling word to the previously-defined word being invoked. The linkage
mechanism --during execution-- uses the return stack (rstack): the
address of the next word to be invoked is placed on the rstack, so
that when the current word is done executing, the system knows to jump
to the next word. (This is so in most, but not all, modern Forth imple-
mentations. But all have a return stack, whether or not they use them
for linking subroutines.)
In addition to serving as a reservoir of return addresses (since words
can be nested, the return addresses need a stack to be put on) the
rstack is where the limits of a DO...LOOP construct are placed.
The user can also store/retrieve to/from the rstack. This is an ex-
ample of using a component for a purpose other than the one it was
designed for. Such use is discouraged for novices since it adds the
spice of danger to programming. See “Note of caution” below.
To store to the rstack we say >R , and to retrieve we say R> . The
word R@ copies the top of the rstack to the TOS.
Why use the rstack when we have a perfectly good parameter stack to
play with? Sometimes it becomes hard to read code that performs com-
plex gymnastics on the stack. The rstack can reduce the complexity.
Alternatively, VARIABLEs —named locations— provide a place to store
numbers —such as intermediate results in a calculation— off the
stack, again reducing the gymnastics. Try this:
\ YOU DO THIS \ EXPLANATION
VARIABLE X <cr> ok \ create a named storage location X;
\ X executes by leaving its address
3 X ! <cr> ok \ ! ("store") expects a number and
\ an address, and stores the number to
\ that address
X @ . <cr> 3 ok \ @ ("fetch") expects an address, and
\ places its contents in TOS.
However, Forth encourages using as few named variables as possible.
The reason: since VARIABLEs are typically global —any subroutine can
access them— they can cause unwanted interactions among parts of a
large program.
Although Forth can make variables local to the subroutines that use
them (see “headerless words” in FTR), the rstack can often replace
local variables:
> The rstack already exists, so it need not be defined anew.
> When the numbers placed on it are removed, the rstack shrinks,
reclaiming some memory.
A note of caution: since the rstack is critical to execution we mess
with it at our peril. If we use the rstack for temporary storage we
must restore it to its initial state. A word that places a number on
the rstack must remove it —using R> or RDROP (if it has been defined)
— before exiting that word. Since DO...LOOP also uses the rstack,
for each >R folowing DO there must be a corresponding R> or RDROP
preceding LOOP. Neglecting these precautions will probably crash
the system.
RDROP is not an ANS Forth word that can be assumed predefined on any system.
Since it is not Standard, some systems call it R>DROP (which also is not
Standard). Here is its definition if needed:
: RDROP ( or R>DROP) ( r: n -- ) R> DROP ;
d. Local variables and VALUEs
I mentioned VARIABLEs above—a VARIABLE is a subroutine whose action is to
return the address of a named, cell-sized memory location, as in
VARIABLE x
x . 247496 ok ( it doesn't have to be this address!)
-49 x !
x @ . -49 ok
A VALUE is a widely used hybrid of VARIABLE and CONSTANT (see below). We
define and initialize a VALUE as we would a CONSTANT:
13 VALUE thirteen ok
We invoke the new VALUE just as we would a CONSTANT:
thirteen . 13 ok
However, we can change a VALUE as though it were a VARIABLE:
47 TO thirteen ok
thirteen . 47 ok
Needless to say, the word TO also works within word definitions, replacing
the VALUE that follows it with whatever is currently in TOS. (Note that
it would be dangerous to follow TO with anything but a VALUE !!) VALUEs
are part of the ANS Forth CORE EXTENSION wordset (that is, the corresponding
code is not guaranteed to be loaded on minimal ANS-compliant systems).
This is a good time to mention that Forth does no type-checking (unless you add
it yourself). YOU must check that TO is followed by a VALUE and not something
else.
ANS Forth also includes a LOCALS EXTENSION wordset that implements named memory
locations local to a word definition. Locals are generally dynamic in nature (that
is, their memory is reclaimed upon exiting the word), although the Standard does
not insist on this. A commonly used syntax is LOCALS| a b c ... |, as in this
definition (from a line-drawing algorithm):
: v+ ( a b c d -- a+c b+d)
LOCALS| d c b a |
a c + b d + ;
2 3 4 5 v+ .S [2] 6 8 ok.. ( .S displays the stack without destroying it)
The important things to remember are
> the names a, b, c ... can be any Forth-acceptable strings;
> the local names have meaning only within a word definition;
> the locals are initialized from the stack as shown in v+ above,
and as in the next example:
: test-locals ( a b c -- )
LOCALS| c b a |
CR ." Normal order: " a . b . c .
CR ." Stack order: " c . b . a .
13 TO a 14 TO b 15 TO c \ how TO works
CR ." Changed: " a . b . c
; ok
3 4 5 test-locals
Normal order: 3 4 5
Stack order: 5 4 3
Changed: 13 14 15 ok
> the locals act like VALUEs, not like VARIABLEs, as the above
example makes clear;
> the LOCALS EXTENSION wordset requires LOCALS| ... | to accomodate
(at least) 8 local names.
> LOCALS| ... | is never necessary, nor does it necessarily shorten code, as
the example below makes clear (7 words as opposed to 6 + preamble):
: v+ ( a b c d -- a+c b+d) 2>R R> + SWAP R> + SWAP ;
What it does accomplish is to reduce stack juggling and clarify the code
in some cases.
6. Using memory
As we just saw, ordinary numbers are fetched from memory to
the stack by @ ("fetch"), and stored by ! (store).
@ expects an address on the stack and replaces that address by
its contents using, e.g., the phrase X @
! expects a number (NOS) and an address (TOS) to store it in, and
places the number in the memory location referred to by the address,
consuming both arguments in the process, as in the phrase 3 X !
Double length numbers can similarly be fetched and stored, by
D@ and D!, if the system has these words.
Positive numbers that represent characters can be placed in character
-sized cells of memory using C@ and C!. This is convenient for operations
with strings of text, for example screen and keyboard I/O.
Of course, one cannot put numbers in memory or retrieve them,
for that matter, without a means of allocating memory and of
assigning labels to the memory so allocated.
The Forth subroutines CREATE and ALLOT are the basic tools for
setting aside memory and attaching a convenient label to it. As
we shall see below, CREATE makes a new dictionary entry, as in
CREATE X
Here the new entry has the name X, but it could have been "Joe"
or anything else. The new name is a Forth subroutine that will
return the address of the next available space in memory. Thus
CREATE X ok
X . 247316 ok
HERE . 247316 ok
HERE is a subroutine that returns the address of the next available
space—we note that it is the same as the address of X because no
space has been ALLOTted. We can rectify this by saying
10 CELLS ALLOT ok
and checking with
HERE . 247356 ok
We see that the next available space is now marked as 40 bytes
further up in memory. (Each CELL is therefore 4 bytes or 32 bits
on this system.) In other words, the subroutine ALLOT increases
the pointer HERE by the number of address units you have told
it to allot. You could have said
40 ALLOT
instead of
10 CELLS ALLOT
but the latter is more portable because it frees you from having
to revise your code if you were to run it on a system with 64-bit
or 16-bit cells (both of which are in common use).
By executing the sequence
CREATE X 10 CELLS ALLOT
we have set aside enough room to hold 10 32-bit numbers--for example
a table or array--that can be referenced by naming it. If we want to
get at the 6th element of the array (the first element has index 0,
so the 6th has index 5) we would say
X 5 CELLS +
to compute its address. To see how this works, let us say
137 X 5 CELLS + ! ok
to store an integer into the 6th array location; then
X 5 CELLS + @ . 137 ok
retrieves and displays it.
Using the tools provided by CREATE and ALLOT we can devise
any sort of data structure we like. This is why Forth does
not provide a panoply of data structures, such as are to be
found in languages like C, Pascal or Fortran. It is too easy
in Forth to custom tailor any sort of data structure one
wishes. In the section on CREATE...DOES> below you will see
that Forth makes it easy to write subroutines ("constructors")
that create custom data structures--that can even include
code fragments that do useful things. For example, a CONSTANT
is a number you would not want to change during a program's
execution. So you do not want access to its memory location.
How then do you get the number when you need it? You package
the code for @ with the storage location, so that by naming
the CONSTANT you retrieve its contents. Its usage is
17 CONSTANT seventeen ok
seventeen . 17 ok
7. Comparing and branching
Forth lets you compare two numbers on the stack, using relational
operators ">", "<", "=" . Thus, e.g., the phrase
2 3 > <cr> ok
leaves 0 ("false") on the stack, because 2 (NOS) is not greater than 3
(TOS). Conversely, the phrase
2 3 < <cr> ok
leaves -1 ("true") because 2 is less than 3.
Notes: In some Forths “true” is +1 rather than -1.
Relational operators consume both arguments and leave a “flag”
to show what happened.
(Many Forths offer unary relational operators "0=", "0>" and "0<".
These, as might be guessed, determine whether the TOS contains an
integer that is 0, positive or negative.)
The relational words are used for branching and control. For example,
: TEST 0 = INVERT IF CR ." Not zero!" THEN ;
0 TEST <cr> ok ( no action)
-14 TEST <cr>
Not zero! ok
The TOS is compared with zero, and the INVERT operator (bitwise logical
NOT—this flips "true" and "false") is applied to the resulting flag. The
word CR issues a carriage return (newline). Finally, if TOS is non-zero,
IF swallows the flag and executes all the words between itself and the
terminating THEN. If TOS is zero, execution jumps to the word following
THEN.
The word ELSE is used in the IF...ELSE...THEN statement: a nonzero
value in TOS causes any words between IF and ELSE to be executed, and
words between ELSE and THEN to be skipped. A zero value produces the
opposite behavior. Thus, e.g.
: TRUTH CR 0 = IF ." false" ELSE ." true" THEN ;
1 TRUTH <cr>
true ok
0 TRUTH <cr>
false ok
Since THEN is used to terminate an IF statement rather than in its
usual sense, some Forth writers prefer the name ENDIF.
8. Documenting and commenting Forth code
Forth is sometimes accused of being a "write-only" language, i.e. some
complain that Forth is cryptic. This is really a complaint against
poor documentation and untelegraphic word names. Unreadability is
equally a flaw of poorly written FORTRAN, PASCAL, C, etc.
Forth offers programmers who take the trouble tools for producing ex-
ceptionally clear code.
a. Parenthesized remarks
The word (*Note: the word POSTPONE in this context means that the word following it —in this case F> — will be compiled into the word that uses MoreThan rather than in MoreThan itelf. (Note that MoreThan is IMMEDIATE.) This way of doing things saves some overhead during execution. Some Forths (notably Win32Forth) define a word SYNONYM to accomplish the same thing.
14. Some remarks about strings As in other languages, alphanumeric strings in Forth are represented as contiguous arrays in memory, each memory unit being a “character”. Traditionally a character encoded by the ASCII or EBCDIC systems occupied one (1) byte of storage, allowing for 256 characters. With the need to encode alphabets other than the Latin one (e.g. Chinese, Arabic, Hebrew, Cyrillic) a two-byte encoding called Unicode has been adopted, which allows for 65535 distinct characters. A traditional Forth string consisted of a count byte and up to 255 bytes containing alphanumeric characters (usually in ASCII). In ANS Forth this scheme has been abandoned: how strings are stored will depend on the implementation. However ANS Forth contains words that enable us to manipulate strings without reference to how they are implemented. Most ANS Forths (and Win32Forth is one of them) define S" to have defined interpretive as well as compiling behavior. This means that if we say S" This is a string!" CR TYPE we get This is a string! ok What happened? S" This is a string!" created a string with text beginning at a “c-address” and with a “count” that says how many characters (including blanks) the string includes. The address and count are left on the stack. That is, the proper stack picture would be S" This is a string!" ( -- c-addr u) (the count is an unsigned integer u because strings of negative length are meaningless). The word CR means “insert a carriage return”, and TYPE means “from the c-addr output u characters to the screen”. Exercise: Use what you have just learned to write a “Hello world!” program. It is perfectly feasible to define one's own word set for working with strings, depending on what sort of application one is writing. For example, I have written a program to translate mathematical formulas in Fortran-like form into Forth code, outputting the result either to the screen (for test purposes) or embedding it into a Forth definition. There is even a variant that evaluates the formula, provided all the variables have been previously defined and given numerical values. To accomplish this required strings longer than 255 characters, so I defined my own. I now want to turn to “pictured numerical output”. Many computer programs need to output numbers in some particular format, no matter how they are stored intern- ally. For example an accounting program might output monetary amounts in the usual dollars-and-cents format. The Forth words that accomplish this are # , <# , #S , #> , SIGN and HOLD They do not have any defined interpretive behavior (although there is no telling what any particular Forth may do) and are intended to be used within word definitions. Here is an example: suppose we are writing an accounting program. Since most users will not be dealing with amounts that exceed $100,000,000 we can use signed 32-bit integers to represent the dollars and cents. (Such numbers can represent amounts up to ±(231—1) = ±2147483647 cents.) Signed double-length integers are at least 32 bits long on all ANS-compatible systems (although they will be 64 bits on 32-bit computers). Hence we shall use doubles so the program will run on any ANS-compatible Forth. A double-length integer is entered from the keyboard by including a decimal point in it, as -4756.325 ok Let us define a word to output a double-length integer. The first part will be to translate it to an alphanumeric string referred to by c-addr u. : (d.$) ( d -- c-adr u) TUCK DABS <# # # [CHAR] . HOLD #S ROT SIGN #> ; As the stack comment ( d -- c-adr u) shows, (d.$) consumes a (signed) double-length integer from the stack and leaves the string data in a form that can be printed to the screen by the word TYPE. Let us test this: 4376.58 (d.$) CR TYPE 4376.58 ok -4376.99 (d.$) CR TYPE -4376.99 ok It is worth exploring what each part does. A double length integer is stored as two cells on the stack, with the most-significant part on TOS. Thus the word TUCK places the most-significant part (containing the algebraic sign) above d and then DABS converts d to |d|. Next, <# begins the process of constructing an alphanumeric string. The two instances of # peel off the two least-significant digits and put them in the string. The phrase [CHAR] . HOLD adds a decimal point to the string. [CHAR] builds in the representation of the character . as a numeric literal (in ASCII it is 46). HOLD then adds it to the string under construction. (HOLD has no meaning except between <# and #>.) Then the word #S takes the rest of the digits and adds them to the nascent string. (Semi)finally, ROT puts the most significant part of d (with its sign) on TOS, and SIGN adds its algebraic sign to the beginning of the string. (Again, SIGN is only meaningful between <# and #>.) And finally, the word #> cleans everything up and leaves c-addr u on the stack, ready for display or whatever. Exercises: a) How would you add a leading dollar sign ($) to the output number? b) How would you enclose a negative amount in parentheses rather than displaying a — sign? [That is, ( 4376.99) rather than -4376.99.] c) Define a word to display a double-length integer in dollar-and-cents format. 15. Assembly language programming Most Forths include an assembler that makes programming in machine code almost as easy as programming in high level Forth. Why would one want to do that? There are reallly only two reasons for dropping into machine language: > One must perform a task requiring carnal knowledge of the hardware; > Part of the program must be optimized for speed. In this section we deal only with the second reason. We imagine that after careful algorithmic analysis there is no way to further speed up a high level program. However the requirements of the application demand a substantial speed improvement. Since most Forths are somewhat inefficient relative to optimized C or Fortran, there may be a substantial speed gain to be realized from hand-coding in assembly language. An example is the innermost loop in a linear equations solver. For n equations it is executed n3 times. Moreover it is a very simple loop, containing 2 fetches, a multi- plication, a subtraction and a store. Thus it is a perfect candidate to be optimized. By contrast, the middle- and outermost loops are executed respectively n2 and n times, so there is little point in optimizing them (that is, for small matrices the running time is too short to care; whereas for large matrices— n > 100 —the middle loop would have to run 100× faster to be worth rewriting in machine code. It is important to realize that assembly language conventions differ from Forth to Forth. Moreover the instruction set will be particular to a given target computer. That is, there is no such thing as a generic assembler in any programming environment, much less for Forth. Hence everything we do here will be specific to Win32Forth running on a Pentium-class machine. We begin with a little warmup exercise. Suppose I found that my program used the sequence * + many times. Obviously good factoring practice would dictate that this sequence be given its own name and defined as a new subroutine (word). So we might define : *+ * + ; and substitute it for the sequence * + throughout the program. But suppose we discover that this short sequence is the bottleneck in our program's running time, so that speeding it up will greatly increase speed of execution. (I realize it isn't likely for this example---bear with me!) So we would like to translate it into machine code. To do this we first look at the machine code for * and + separately. These are primitive words and almost certainly will be CODE definitions in any reasonable Forth. Thus we need to disassemble these words. In some Forths this might mean inspecting the contents of the word byte by byte, and looking up the code sequences in the operating manual for that cpu. Fortunately for us, Win32Forth has a built-in disassembler. If we SEE a CODEd definition it will return the actual byte-codes as well as the names of the instructions in the Win32Forth assembler. Let us try this out: we get see + + IS CODE 4017AC 58 pop eax 4017AD 03D8 add ebx, eax ok see * * IS CODE 401B9C 8BCA mov ecx, edx 401B9E 58 pop eax 401B9F F7E3 mul ebx 401BA1 8BD8 mov ebx, eax 401BA3 8BD1 mov edx, ecx ok To understand these sequences we must bear in mind that Win32Forth keeps TOS in a 32-bit register, in fact the ebx register. We must also know that Win32Forth uses the edx register for something or other—probably to do with the mechanism for executing a word and returning control to the next word in the program (that is, the threading mechanism). So if a program is going to modify the edx register, its previous contents have to be saved somewhere. Since addition of eax to ebx does not affect edx, the CODE for + doesn't need to protect edx; however, when two 32-bit numbers are multiplied, the result can contain as many as 64 bits. Thus the product occupies the two registers eax (bits 0 through 31) and edx (bits 32-63). This is the reason for saving edx into the unused ecx register, and then restoring it afterward. It is worth noting, before we go too far, that the Win32Forth assembler preserves the Intel conventions. That is, add ebx, eax adds the contents of register eax to ebx, leaving the result in ebx (which is where we want it because that is TOS). Similarly, the sequences mov ecx, edx and mov ebx, eax have the structure mov destination, source We should also ask why the integer multiplication instruction mul ebx has only one operand. The answer is that the register eax is the so-called “accumulator”, so it contains one of the multiplicands initially and then it and edx contain the product, as noted above. It is then only necessary to specify where the other multiplicand is coming from (it could be a cell in memory). Therefore to define the word *+ in assembler we would type in CODE *+ ( a b c -- b*c+a) \ stack: before -- after mov ecx, edx \ protect edx because mul alters it pop eax \ get item b; item c (TOS) is already in ebx mul ebx \ integer multiply-- c*b -> eax (accumulator) pop ebx \ get item a add ebx, eax \ add c*b to a -- result in ebx (TOS) --done mov edx, ecx \ restore edx next, \ terminating code for Forth interpreter END-CODE ok Note that the Forth assembler recognizes Forth comments—Intel-style comments would be preceded by semicolons, but we obviously can't use these because semicolon is a Forth word. The word END-CODE has an obvious meaning, but what about next, (the comma is part of the name and is significant!). Advanced users of the assembler sometimes need to define code sequences that do not include the instructions to transfer control to the next word. So Win32Forth has factored this function out of the CODE terminating sequence. For this example we require these instructions to be assembled, so we include next, . Before going further, you should try out this example and convince yourself it works. For our nontrivial example we are going to hand-code the innermost loop of my linear equations solver. I programmed this in high-level Forth in the form : }}r1-r2*x ( M{{ r1 r2 -- ) ( f: x -- x) \ initialize assumed 0 0 LOCALS| I1 I2 r2 r1 mat{{ | \ local names frame| aa | \ local fvariable Iperm{ r1 } @ TO I1 Iperm{ r2 } @ TO I2 Nmax r2 ?DO \ begin loop f" mat{{ I1 I }} = mat{{ I1 I }} - mat{{ I2 I }} * aa" LOOP \ end loop f" aa" |frame ( f: -- x) ; Here Iperm{ is the name of an array of integers that holds the permuted row-labels; note that the rows we work on do not change within the actual loop. Neither does the floating point number represented by the local variable aa. What does change are the row-elements. To translate }}r1-r2*x to assembler we will need to factor it a bit more finely. Evidently we are subtracting the I'th element of row I2, multi- plied by aa, from the I'th element of row I1. Moreover, since the matrix has been partially triangularized already, we do not start with element 0 but with element r2. Finally, as we have noted previously, ?DO includes a bounds check so that if r2 equals or is greater than Nmax the loop is not executed. So we shall revise }}r1-r2*x to include this test explicitly and CODE only the loop itself. That is, we shall write : incr_addrs ( addr1 addr2 -- addr1+inc addr2+inc) [ 1 FLOATS ] LITERAL TUCK + -ROT + SWAP ; : inner_loop ( addr1 addr2 Nmax lower_limit -- ) ( f: x -- x) DO \ begin loop ( f: aa) ( addr1 addr2) \ loop invariant 2DUP SWAP F@ ( f: aa m[I1,I]) FOVER F@ F* F- OVER F! \ m[I1,I = m[I1,I] - m[I2,I]*x ( f: x) ( addr1 addr2) \ loop invariant incr_addrs \ increment addresses LOOP \ end loop 2DROP ; : }}r1-r2*x ( M{{ r1 r2 -- ) ( f: x -- x) \ initialize assumed 0 0 LOCALS| I1 I2 r2 r1 mat{{ | \ local names Iperm{ r1 } @ TO I1 Iperm{ r2 } @ TO I2 Nmax r2 > IF mat{{ I1 r2 }} mat{{ I1 r2 }} \ base adresses Nmax r2 \ loop limits ( f: x) ( addr1 addr2 Nmax lower_limit) inner_loop ( f: x) ( -- ) THEN ; So what we are going to CODE here is the word inner_loop, since these are the only instructions executed n3 times. CODE inner_loop ( addr1 addr2 Nmax lower_limit -- ) ( f: x -- x) fld FSIZE FSTACK_MEMORY \ f: -> fpu: mov ecx, ebx \ ecx = r2 pop eax \ eax = Nmax ( addr1 ebx=addr2) push edx ( addr1 edx ebx) mov edx, 4 [esp] \ edx = addr1) \ begin loop L$1: fld [ebx] [edi] ( fpu: aa m[addr2] fmul st, st(1) ( fpu: aa m2*aa) fld [edx] [edi] ( fpu: aa m2*aa m1) fxch st(1) ( fpu: aa m1 m2*aa) fsubp st(1), st ( fpu: aa m1-m2*aa) fstp [edx] [edi] ( fpu: aa) add [edx], # 8 \ increment addresses add [ebx], # 8 inc ecx \ add 1 to loop variable cmp eax, ecx \ test for done jl L$1 \ loop if I < Nmax \ end loop pop edx \ restore edx pop ebx pop ebx \ clean up data stack fstp FSIZE FSTACK_MEMORY \ fpu: -> f: next, END-CODE A final remark: I have written a tool for translating automatically a sequence of floating point operations to CODE for the Intel fpu. This tool, ctran.f, is specialized for Win32Forth. 16. Some useful references > M. Kelly and N. Spies, Forth: A text and Reference (Prentice-Hall, NJ, 1986)
> L. Brodie, Starting Forth, 2nd ed. (Prentice-Hall, NJ, 1986)
> L. Brodie, Thinking FORTH (Prentice-Hall, NJ, 1984 (online edition)