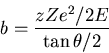Rutherford Scattering in Classical Mechanics

Assume the scattering center to be infinitely massive, and represented by a potential energy term:

$$V(r) = \frac{Z z e^2}{r}$$

where $Z$ is the number of protons in the target nucleus, and $z$ is the number of protons in the beam nucleus, e.g. $z=2$ for the $\alpha$ particle.

Among the conserved quantities for the scattering process, Rutherford noticed that there was also $\epsilon$, the so-called $Runge-Lenz$ vector also used in the description of Kepler laws:

$$\epsilon = \frac{-1}{Z z e^2 m} {\bf L} \times {\bf p} + \frac{\bf r}{r}$$

${\bf L}$ being the angular momentum, and ${\bf p}$ the momentum. By taking the dot product of $\epsilon$ with ${\bf r}$, one has:

$$\epsilon \cdot {\bf r} \equiv \epsilon r cos \phi \frac{L^2}{Z z m e^2} + r$$

This equation can be identified with the polar equation for a hyperbola of eccentricity $\epsilon$:

$$r = \frac{ (- L^2/Z z me^2)}{1 - \epsilon \cos \phi}$$

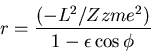
The angle between the asymptotes of the hyperbola is then defined by taking the poles in the denominator, as:

$$\sin \theta/2 = 1/\epsilon$$

From this, noticing that the impact parameter, or the distance between the scattering center and the asymptotic direction of the particle, is:

$$b= \frac{L}{\sqrt{2mE}}$$

$E$ being the kinetic+potential energy of the particle, one obtaines the following relation between $b$ and $\theta$:

$$b = \frac{z Ze^2/2E}{\tan \theta/2}$$