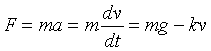
Understanding and Using Newton’s Laws
Real-World Falling
Newton’s laws are certainly very simple to state: an object will continue to move at constant velocity in the absence of outside force, F = ma, and action = reaction. But really understanding them takes a good deal of experience in applying them in real situations!
We shall examine in detail the one-dimensional example of a falling object where we include the effect of air resistance. We shall do this in two ways: since this is a calculus based course, we first show how to do it using calculus. But then we will do it numerically, using an Excel spreadsheet. It is perhaps easier to get the fundamental concepts across using the spreadsheet, and in fact it is easily adaptable to more complicated drag forces which cannot be treated analytically.
One-dimensional Motion Revisited: Calculus Treatment
As an example of how Newton’s Laws can give us quantitative dynamical information, let us look again at a falling object, but this time we’ll include the force generated by air resistance. We already know this force increases with velocity, and that the body will approach a terminal velocity, if it falls for long enough time. But Newton’s Laws lead to much more information—if we know how the resisting force varies with velocity, we can work out exactly how the velocity increases with time.
Suppose, for example, that the force is proportional to the velocity (it’s obviously in the opposite direction!),
Fdrag = -kv
where k is a constant. Then Newton’s Second Law gives
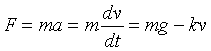
This is a straightforward integral, giving![]()
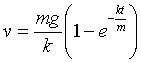
Exercise: Do the integral. Find the behavior of v for small t. Explain your result physically. Now write v = dx/dt to find an integral for the distance fallen as a function of time, and do it.
In fact, the force is only proportional to the velocity for a slow moving object that leaves no wake, experimentally the force is proportional to the square of the velocity in most situations. So the equation is:
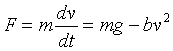
We can see that this will give a terminal velocity v0 given by mg = bv02. The above equation can be rearranged to read:
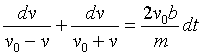
This can be integrated, and fixing the constant of integration by the requirement that the velocity be zero at t = 0 we find:

Exercise: Do the integral. Find the behavior of v for small t. (If you’re familiar with the hyperbolic tangent, you’ll notice that the result can be expressed as ![]() , and this can then be integrated to give an expression for distance as a function of time.)
, and this can then be integrated to give an expression for distance as a function of time.)
Copyright © 1998 Michael Fowler