In this lecture we shall expand on some of the topics raised in the Physics 109 lecture Momentum, Work and Energy—discussing potential energy for pendulums, springs, and planets, and giving the more general derivation of the expression for kinetic energy.

In the last lecture, we talked about raising a hammer of mass m through a height h from the floor, showed that took work mgh, and stated that energy mgh was now stored in the hammer by virtue of its new elevated position, and would be transformed into kinetic energy if the hammer were now to be dropped back to the floor. So, the hammer at height h above the floor had potential energy mgh. With this line of reasoning, the hammer obviously has zero potential energy while it’s still on the floor. But in a way that’s not true—unless you’re in the basement, you could cut a hole in the floor and drop the hammer through it, and it would certainly gain kinetic energy. (If you are in the basement, you could dig a well.)

We could still come up with a consistent accounting of the transfer of potential energy to kinetic energy by deciding that as the hammer drops through the floor and/or down the well it’s gaining negative potential energy. In other words, we stick with our definition of potential energy mgh measured from the original floor, but h’s measured down from that floor level are counted as negative. Of course, this renders the picture of potential energy as stored energy a little less intuitive.

 What is really important in these scenarios of raising and dropping objects is the difference in potential energy between two heights. That is what measures how much work you have to do, and how much kinetic energy is generated in falling. And to measure differences, it doesn’t matter where you take the zero of potential energy to be—at the original floor level, the floor below, or the bottom of a well in the basement. So the answer to the question of where the potential energy is zero is: anywhere you want it to be—but you only get to choose once! As will become clear below, the most convenient choice of where to set it zero varies with the system.

 The conservation of energy, P.E. + K.E. = constant can be widely applied in problems on falling, projectiles, planetary motion, etc. It must always be borne in mind, though, that this neglects frictional effects. It is manifestly not true for an object falling at terminal velocity!

For a pendulum of ordinary size swinging through small angles in air, frictional effects are quite small, and the motion can be understood as a continuing periodic exchange between kinetic energy and potential energy.

 Let us take the zero of potential energy to be at the bottom of the swing, and first ask what is the potential energy when the pendulum is at a (small) angle q to the vertical. The potential energy is, of course, entirely from gravity, so recalling our discussion in the last lecture, the only thing that matters is that the pendulum is slightly higher than at the bottom of the swing, and the potential energy is equal to the weight of the pendulum multiplied by the change in height. If the pendulum has length L, the change in height is L(1 - cosq ). For small q , we can write cosq = 1 – ½q ².

Thus for a pendulum swinging through small angles,

P.E. = ½mgLq ²

It is also worth seeing how this result comes about by just pushing on the pendulum. If I push the pendulum aside to an angle q , and hold it there, my push being always in the direction the pendulum naturally moves, what force do I feel? For tiny changes in angle near angle q , this is just like pushing something up a smooth ramp having incline angle q . Thus the force I must supply to keep the pendulum in place is just mgsinq , and for small angle swings this is to a good approximation just mgq .

 Now, this (small angle) force is linear in q , and hence linear in distance traveled from the bottom point—that distance being Lq , (q as usual in radians). Since the force increases linearly with distance, the total work done in displacing the pendulum from the lowest point to the angle q is just the average force x the distance moved, 

work done = ½mgq x Lq = ½mgLq ² 

This is of course equivalent to the earlier derivation. It’s a good idea to sketch the potential energy as a function of q , and picture this as a valley the pendulum slides backwards and forwards in, trading potential energy for kinetic energy and then vice versa.

 Neglecting friction as usual, the energy conservation equation is: 

½mv² + ½mgLq ² = constant, 

or, introducing the angular velocity w , so that v = Lw ,  

½mL²w ² + ½mgLq ² = constant. 

It should be mentioned at this point that the kinetic energy of a rotating object is written in terms of its angular speed w and its moment of inertia I as ½Iw ². Note that the pendulum kinetic energy has just this form with I = mL².

As stated above, if a pendulum is at a small angle q to the vertical, the component of the force of gravity tending to push it back along its path

F = -mgq .

It is convenient to work in terms of arc length, in other words displacement along the curved path of the pendulum measured from the bottom, call this s. Then s = Lq .

 Newton’s Second Law F = ma becomes:

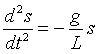
(the m’s on both sides cancel). This differential equation has the solution 

s = A sin w t, where w ² = g/L.

This sinusoidal dependence of displacement on time is called Simple Harmonic Motion. The reader should check this solution by substituting it in the differential equation.

Suppose now we have a mass at rest hanging on a spring. We will assume the spring obeys Hooke’s law, that is, when it is extended x meters beyond its natural length, it exerts a force -kx on whatever is holding it taut. If the spring is extended x₀ meters when the mass is hanging at rest, with no other forces present, the spring must be exerting an upward force exactly equal to the weight, so

kx₀ = mg.

If we now stretch the string to some different length x, and let it go, then at that instant the spring force and the weight will no longer be in balance, the net upward force the spring exerts on the weight being

kx - mg = k(x-x₀)

That is to say, if the mass is displaced from the equilibrium position x₀, it will feel a restoring force towards that position which is directly proportional to the mass’s displacement.

Newton’s Second Law for the mass on the spring is then:

,

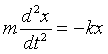which has the same simple harmonic solution as the small-angle pendulum above, with now w ² = k/m.

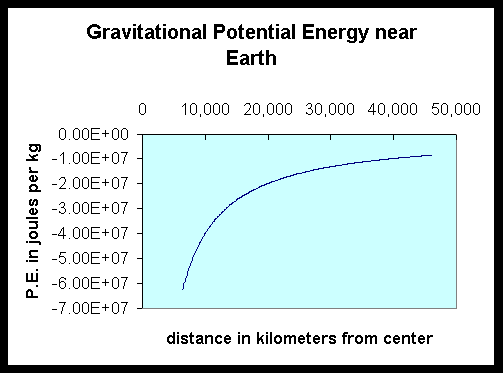
We now consider a more complicated—but very important—force law, the inverse-square force of gravity. How much energy does it take to put a satellite in orbit? Let’s examine here the amount of potential energy gained by a mass m raised from the earth’s surface at r₁, say, to a high orbit r₂, against an attractive gravitational force GMm/r².

It’s evident on glancing at this graph of force versus distance that the force at a point midway between the earth’s surface and a height of, say, 40,000km is not the average force over that distance. Therefore, the simple arguments we could use to find the total work for displacing the pendulum, based on the average force being equal to the force at the midpoint, are not going to work here. We have to take a more careful approach. We must raise the mass m in small steps, find the work expended in each step, and add them all up.

So, how much work does it take to raise the mass from r to r + Dr? A good approximation is

Force x distance = GMm/r² x Dr

Of course this isn’t perfect—the force is going down as we move from r to r + Dr, and we’ve just taken its value at r. We get a much better approximation if we average the force by taking not r², nor (r+Dr)² in the denominator, but the intermediate value r(r+Dr). Furthermore, with this choice, the equation takes a simpler form:

Work needed = GMm/r(r + Dr) x Dr = GMm(1/r – 1/(r + Dr)).

We’re now ready to find the total work needed to raise a mass m from the earth’s surface at r₁ to some distant point r₂. We divide the distance r₁ to r₂ into a large number N of equal small intervals each of length Dr. That is to say, we first raise the mass from r₁ to r₁ + Dr, then from r₁ + Dr to r₁ + 2Dr, from there to r₁ + 3Dr ,…, finally to r₁ + NDr = r₂.

This is not as bad as it sounds, because we have managed to write the work needed for a single step as a difference between functions at the two ends, and consequently when we add all the steps together, everything except the ends cancels! Explicitly, we get:

Work from r₁ to r₂ =

GMm{(1/r₁–1/(r₁ + Dr)) + (1/(r₁+Dr)–1/(r₁ + 2Dr)) + … + (1/(r₁+(N-1)Dr –1/(r + NDr))}

=GMm(1/r₁ – 1/r₂)

If r₂ is very close to r₁, in other words we stay near the earth’s surface, this becomes approximately GMm(r₂-r₁)/r₁². This is just the familiar mgh, with r₂ – r₁ = h, and GM/r₁² = g.

Notice that even if we let r₂ go to infinity, it only takes a finite amount of work to get there! (Time might be a problem.) What this means is that the earth’s gravitational pull weakens with distance rapidly enough that a rocket leaving the atmosphere with sufficient speed will never be pulled back. The minimum speed for this one way trip to happen is called the escape velocity. It is evident that escape velocity is given by

½mv² = GMm/r₁

where r₁ has to be a few miles up, so that atmospheric drag is negligible.

The most natural place to take the zero of potential energy for the earth’s gravitational field is somewhere where it has no effect, that is, far away. This means that the potential energy of a mass is always negative—the earth is at the bottom of a sort of three dimensional cone, so it takes work—it’s uphill—to move away in any direction. The shape of the hill is: