Before analyzing rotational motion, it's worth considering what patterns of forces cause rotation. For example, suppose you and I face each other, standing on a slippery floor. We both hold our hands up at shoulder level, say. Then you hold my right hand with your left hand, and my left hand with your right hand. Then at the same time you begin to push on my right hand and pull on my left hand with the same force. What happens? If the floor is slippery enough, we'll both begin to rotate.

Notice, though, that the two forces you're exerting on me are equal and opposite, so you might think Newton's Laws would predict nothing at all would happen, even though we know better. But if you look back at the notes on static equilibrium, the statement was that there will be no change of motion if the forces add up to zero and if the forces act at the same point. Even if the forces don't act at the same point, if they add to zero, the body acted on won't move away - that is to say, its center of mass will stay put. But it will, in general, begin to rotate, unless frictional forces come into play to balance the applied forces.

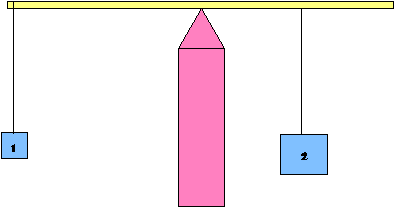
To make any more progress, we need to find some quantitative criterion for when forces on a body, which do add to zero, are also in rotational equilibrium - that is, they won't cause the body to begin to rotate. A familiar example of a body having forces applied at different points is the seesaw. Let's say we have a seesaw carrying two children, one weighing 20 kg and one weighing 40 kg, and that the seesaw is at rest, balanced. As everybody knows, this happens when the 20 kg child sits twice as far from the middle as the 40 kg child, assuming that the seesaw itself is balanced when nobody is sitting on it.

Let's now analyze what's going on in terms of the forces acting on the seesaw. Take the seesaw itself to be a uniform horizontal plank, with an axle through its midpoint, the balance point or fulcrum. If a child sits on one end, with nobody on the other end, the seesaw will certainly begin to rotate, and plonk the child down on the ground. This will also happen if two children of different weights sit at equal distances from the middle on opposite sides. But we know from experiment that there will be no rotational motion if two children of different weights sit at different distances such that the ratio of the distances is the inverse of the ratio of their weights. In other words, the 20 kg child must sit exactly twice as far from the center as 40 kg child, and the seesaw will balance.

This is the principle of the lever, first spelled out by Archimedes. The two downward forces, the weights of the two children, both tending to rotate the horizontal seesaw, will cancel each other, so there will be no rotation, if they have the same amount of leverage, defined as the magnitude of the force multiplied by the distance from the center of the point where it operates. This leverage goes under several names: it is also called the torque, and sometimes the moment of the force. Actually, this definition needs to be made a little more precise, in that we need to keep track of which way the forces tend to rotate the seesaw. It won't balance if both children sit on the same side of the middle. We could count the leverage as positive if the force is tending to rotate the seesaw clockwise. It doesn't matter what convention you choose, as long as you stick to it when adding up the effect of all the forces involved.

The simplest way to make all this clear is to hang weights from a meter stick (or any uniform rigid stick), supported at its midpoint, perhaps by having a rod through a hole in it, so that it's free to rotate in a vertical plane. Several weights could be hung at different distances from the center. In this way, it can be verified experimentally that when the beam is at rest, the total moment-the sum of weights multiplied by their individual leverage distances-tending to rotate the stick clockwise just equals the total moment tending to rotate the stick anticlockwise.

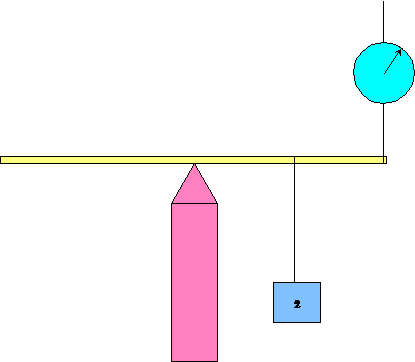There's also a simple extension of this experiment to include upward forces on the meter stick. We can pull upwards on it with a piece of string tied around it, using a spring scale to measure the tension in the string.

In the case illustrated, with the string twice as far from the middle as the 2 kg mass, the tension in the string is equivalent to 1 kg weight, that is, 10 newtons (taking g = 10). A more interesting case arises when the string is not perpendicular to the meter stick.

In this situation, the tension T in the string is greater than 10 newtons. It is easy to see why if we split the vector force of the string tension acting on the meter stick into two components, one along the stick and one perpendicular to it. The component along the stick does not tend to turn the stick around the fulcrum. Assuming the connection between the stick and the fulcrum stays firm, this force has no effect. (It is balanced by a sideways force between the fulcrum and the stick.) The component of the string tension force perpendicular to the meter stick acts to cause rotation in the usual way. Therefore, if the string is at an angle q to the stick, the moment of the force about the fulcrum is Tdsinq , where d is the distance of the point of application from the fulcrum.

This quantity is often called the torque,

and can also be thought of as being the full force of magnitude T multiplied by the "leverage arm", meaning the perpendicular distance from the fulcrum to the line the force acts along. That distance is dsinq . (Exercise: check that this is true in the above diagram.)

A useful geometrical representation of the magnitude of the torque is that it is just twice the area of the triangle formed by the force vector (in its correct position of application to the body being acted on) and the point around which the body is free to rotate.

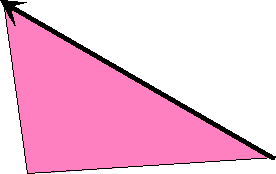
(Exercise: check that this follows from the above definition).

To understand forces in rotational equilibrium a little more clearly, it is worthwhile to take some flat object free to move on a smooth table top, and attach three strings to arbitrary points. Now have three people pulling one on each string, holding the object stationary. Whatever forces are used, if the object is at rest it will be found that the lines of the strings all pass through the same point (or are exactly parallel, which is equivalent to passing through a point far away).

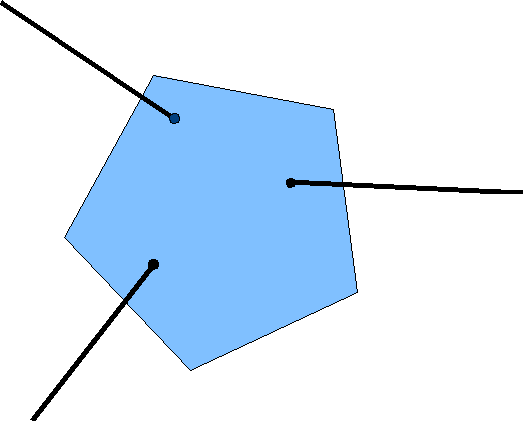This is a little trickier than the previous examples, because since the body is free to move horizontally there is no obvious pivot point to find the torques around. In fact, though, if the forces acting on a body have a nonzero total torque about any point, the body will begin to rotate about that point. Since the lines of application of two of the forces meet in a point, the body will begin to rotate if the third force has a nonzero torque about that point. It follows that if the body is at rest all three force lines pass through the same point. (Of course, the forces must also add vectorially to zero, or the body will accelerate linearly across the table.)

Let us consider the simplest situation of a wheel rotating at a steady rate about an axle. Suppose that a mass M is attached to the rim of the wheel. We want to understand the motion of the mass M in terms of the rotation. It goes in a circle, of course, but how fast is it moving?

If the wheel is rotating at n revolutions per second, then in one second the mass travels 2p rn meters per second, so v = 2p rn. For a more slowly rotating wheel, moving only a small fraction of a revolution in a second, it might be more convenient to measure the rotational speed in degrees per second, with 360 degrees being a complete revolution. If the wheel moves through p degrees per second, the relationship between the speed v of the mass M and the rotational speed is v = 2p rp/360.

Evidently, any formula of this kind relating speed of the mass to angular speed contains a 2p on top and a number on the bottom stating how many of the angle units fit around one circle. The way to get the simplest possible formula is to choose a unit of angle such that 2p of them fit around a circle, so the 360 in the formula above will be replaced by a 2p , which will then cancel the 2p on top. This unit of angle is called the radian, and is about 57 degrees. From now on, we shall measure angles in radians unless explicitly stated otherwise, and we shall use the standard symbol for angular velocity, w radians per second.

The relation between velocity v and angular velocity w is then the simplest possible:

Radians are also a natural unit of angle for trigonometry. For example, for small angles sinq = q to a good approximation, if and only if q is measured in radians.

As we have discussed above, if a body at rest is free to rotate about an axis, but the total torque of the forces acting on the body is zero, the body will be in rotational equilibrium and will remain at rest. It is also found experimentally that a body rotating at an angular velocity w will continue to rotate at that rate if the net torque is zero. These findings are the angular equivalents of Newton's First Law. What about the Second Law?

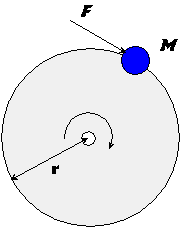
To make a connection between the familiar form of the Second Law, F = Ma for acceleration of a mass by a force, and the angular acceleration of a rotating object by a torque, let us consider the simple case illustrated above, in which a mass M is firmly attached to a disk of negligible mass, so that the mass M must go around in a circle. Let us assume the mass is initially at rest, then the force F is applied. What happens in the first few moments? Well, of course, the mass accelerates with acceleration a = F/M. As soon as it reaches a significant speed, the disk will begin to exert a force towards the center, to keep it on its circular path, but let's just concentrate on the first few moments before that effect becomes important. Let's just translate that initial acceleration into angular language. Since the angular velocity w is related to the actual velocity by v = rw , the angular acceleration a must be related to the ordinary acceleration a along a tangential direction by a = ra . So we can see how to connect the two accelerations, now we must connect the two forces, or, rather, the linear force F with the torque t acting on the system mass + wheel. (The Greek letter t , tau, is the standard notation for a torque.)

Evidently, the torque t is just equal to the force F multiplied by its leverage arm r, that is, t = Fr. Putting this together with a = ra , we find that F = Ma translates to:

t = Fr = Mar = Mr² a

Comparing this equation, t = Mr² a , with F = Ma, we notice that the quantity Mr² plays the role of mass, or inertia, in rotational dynamics. It is called the moment of inertia. Of course, we've only found the "moment of inertia" for a single mass attached to a light disk. What about something more complicated, for example a heavy disk?

The key to finding the moment of inertia for a solid body is to visualize it as a lot of small masses all glued together. Think specifically of a heavy wheel of radius R, rotating about a fixed axle with negligible friction. Imagine the wheel to be initially at rest, then a force F is applied to the rim tangentially, so that the torque is FR. Of course, the whole wheel begins to rotate, so think what happens to one of the small masses we are imagining the wheel to be made up of. If it is at a distance r from the axle, and the initial angular acceleration of the wheel is a , this small mass, D m say, must experience an initial acceleration ra , so there must be a total force on it of D mra , and therefore a torque acting on it of D mr² a . But where, exactly does this torque come from? It must be caused by the force F being applied to a different part of the wheel, but the immediate cause on the small mass D m is just the pulls and pushes of its neighbors. In other words, if you push on one part of the wheel, since it's a solid body its rigidity transmits the effect of the force to all the other parts, so the wheel rotates as a whole, provided the force is not strong enough to tear the wheel apart. Recall that the torque felt by one small part of the wheel was D mr² a , the total torque felt be all the parts of the wheel is just the sum of terms like that,

torque = S D mr² a = ò dmr² a

with the integral being over all the tiny masses dm making up the wheel.

Now comes a crucial point. How do we relate this torque to the external force torque FR? What about all the internal forces-the fact that each part of the wheel feels forces from neighboring parts? How do we take account of this very complicated situation?

The answer is that we don't have to! By Newton's Third Law, all those internal forces are in equal opposite pairs, actions and reactions between neighboring masses. This means that when we sum over all parts of the wheel, we count all these forces, and they all cancel each other in pairs. Therefore the total torque is just that from the external forces.

It follows that the analog of Newton's Second Law for rotation about an axle is

Torque t = Ia

where the moment of inertia I is given by ò dmr²a .

Finding the moment of inertial is now just a matter of doing elementary integrals. For the case of a hoop of mass M, where all the mass can be taken at the same distance R from the axis of rotation, no integral at all is necessary, I = MR². A disk can be thought of as constructed of successive hoops, like a two-dimensional onion. As a practical matter, the best approach is to use the two-dimensional density, call it r , so that the total mass of the disk is density x total area, M = p R²r. Then the "hoop" which is that part of the disk between r and r + dr from the center has mass 2p rdrr , and a straightforward integral gives I = 1/2MR² for the moment of inertia of a disk. The same expression works for a cylinder, which for these purposes is just a stack of disks.