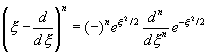The Simple Harmonic Oscillator

Michael Fowler

University of Virginia

Einstein’s Solution of the Specific Heat Puzzle

The simple harmonic oscillator, a nonrelativistic particle in a potential ½Cx², is an excellent model for a wide range of systems in nature. In fact, not long after Planck’s discovery that the black body radiation spectrum could be explained by assuming energy to be exchanged in quanta, Einstein applied the same principle to the simple harmonic oscillator, thereby solving a long-standing puzzle in solid state physics—the mysterious drop in specific heat of all solids at low temperatures. Classical thermodynamics, a very successful theory in many ways, predicted no such drop—with the standard equipartition of energy, ½kT in each mode, the specific heat should remain more or less constant as the temperature was lowered (assuming no phase change). To explain the anomalous low temperature behavior, Einstein assumed each atom to be an independent (quantum) simple harmonic oscillator, and, just as for black body radiation, he assumed the oscillators could only absorb or emit energy in quanta. Consequently, at low enough temperatures there is rarely sufficient energy in the ambient thermal excitations to excite the oscillators, and they freeze out, just as blue oscillators do in low temperature black body radiation. Einstein’s picture was later somewhat refined—the basic set of oscillators was taken to be standing sound wave oscillations in the solid rather than individual atoms (making the picture even more like black body radiation in a cavity) but the main conclusion—the drop off in specific heat at low temperatures—was not affected.

Schrödinger’s Equation and the Ground State Wave Function

The classical equation of motion for a one-dimensional simple harmonic oscillator with a particle of mass m attached to a spring having spring constant C is

.

The solution is

,

and the momentum p = mv has time dependence

The total energy is clearly constant in time.

It is often useful to picture the time-development of a system in phase space, in this case a two-dimensional plot with position on the x-axis, momentum on the y-axis. For dimensional consistency, we would plot mw x against p. It is evident that in these variables, the point representing the system in phase space moves clockwise around a circle of radius centered at the origin.

Note that in the classical problem, we could choose any point x, p, place the system there and it would then move in a circle about the origin. In the quantum problem, on the other hand, we cannot specify the initial x, p precisely, because of the uncertainly principle. The best we can do is to place the system initially in a small cell in phase space, of size . In fact, we shall find that in quantum mechanics, phase space is always divided into cells of essentially this size for each pair of variables.

From the expression for total energy above, the Schrödinger equation for the quantum oscillator follows in standard fashion:

What will the solutions to this Schrödinger equation look like? Since the potential ½mw² x² increases without limit on going away from x = 0, no matter how much kinetic energy the particle has, if it gets far enough from the origin the potential energy dominates, and the (bound state) wavefunction will decay increasing rapidly as x increases further. (Obviously, for a real physical oscillator there is a limit on the height of the potential—we will assume that limit is much greater than the energies of interest in our problem.)

We know that when a particle penetrates a barrier of constant height V₀ (greater than the particle’s kinetic energy) the wave function decreases exponentially into the barrier, as , where . But, in contrast to this constant height barrier, the “height” of the simple harmonic oscillator potential continues to increase as the particle penetrates to larger x. Obviously, in this situation the decay will be faster than exponential. If we (rather naïvely) assume it is more or less locally exponential, but with a local a varying with V₀, neglecting E relative to V₀ in the expression for a suggests that a itself is proportional to x, so maybe the wavefunction decays as ?

To check this idea, we insert in the Schrödinger equation, using

to find

.

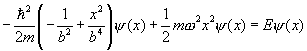The y(x) is just a factor here, and it is never zero, so can be cancelled out. This leaves a quadratic expression which must have the same coefficients of x⁰, x² on the two sides, that is, the coefficient of x² on the left hand side must be zero:

.

This fixes the wave function. Equating the constant terms fixes the energy:

.

So the conjectured form for the wave function is in fact the exact solution for the lowest energy state! (It’s the lowest state because it has no nodes.)

Also note that even in this ground state the energy is nonzero, just as it was for the square well. The central part of the wave function must have some curvature to join together the decreasing wave function on the left to that on the right. This “zero point energy” is sufficient in one physical case to melt the lattice—helium is liquid even down to absolute zero temperature (checked down to microkelvins!) because the wave function spread destabilizes the solid lattice that will form with sufficient external pressure.

Higher Energy States

It is clear from the above discussion of the ground state that is the natural unit of length in this problem, and that of energy, so to investigate higher energy states we reformulate in dimensionless variables,

.

Schrödinger’s equation becomes

.

Deep in the barrier, the e term will become negligible, and just as for the ground state wave function, higher bound state wave functions will have behavior, multiplied by some more slowly varying factor.

The standard approach to solving the general problem is to factor out the term,

giving a differential equation for h(x):

We try solving this with a power series in x : . Inserting this in the differential equation, and requiring that the coefficient of each power x ⁿ vanish identically, leads to a recurrence formula for the coefficients h_n:

.

Evidently, the series of odd powers and that of even powers are independent solutions to Schrödinger’s equation. For large n >>e, the recurrence relation simplifies to . The series therefore tends to . Multiply this by the factor to recover the full wavefunction, we find it diverges as .

Actually we should have expected this—for a general value of the energy, the Schrödinger equation has the solution at large distances, and only at certain energies does the coefficient A vanish to give a normalizable bound state wavefunction.

So how do we find the nondiverging solutions? It is clear that the infinite power series must be stopped! The key is in the recurrence relation: if the energy satisfies 2e = 2n + 1, with n an integer, h_n+2 and all higher coefficients vanish. The remaining n^th order polynomial is called a Hermite polynomial and written H_n(x).

The standard normalization of the Hermite polynomials H_n(x) is to take the coefficient of the highest power x ⁿ to be 2ⁿ . The other coefficients are easy to find using the recurrence relation above, giving:

So the bottom line is that the wavefunction for the n^th excited state, having energy , is , where C_n is a normalization constant to be determined in the next section.

Operator Approach to the Simple Harmonic Oscillator

Having scaled the position coordinate x to the dimensionless x by x = x/b, let us also scale the momentum from p to p = -i d/dx (so ). The Hamiltonian is

Dirac had the brilliant idea of factorizing this expression: the obvious thought isn’t quite right, because it fails to take account of the noncommutativity of the operators, but the symmetrical version

is fine, and we shall soon see that it leads to a very easy way of finding the eigenvalues and operator matrix elements for the oscillator, far simpler than using the wave functions we found above. Interestingly, Dirac’s factorization here of a second-order differential operator into a product of first-order operators is close to the idea that led to his most famous achievement, the Dirac equation, the basis of the relativistic theory of electrons, protons, etc.

To continue, we define new operators by

From the commutation relation it follows that

Therefore the Hamiltonian can be written:

Note that the operator N can only have non-negative eigenvalues, since

Now

Suppose N has an eigenfunction |n> with eigenvalue n,

From the two equations above

so is an eigenfunction of N with eigenvalue n + 1. Operating with again and again, we climb an infinite ladder of eigenstates equally spaced in energy.

is often termed a creation operator, since the quantum of energy added each time it operates is equivalent to an added photon in black body radiation (electromagnetic oscillations in a cavity).

It is easy to check that the state is an eigenstate with eigenvalue n - 1, provided it is nonzero, so the operator a takes us down the ladder. However, this cannot go on indefinitely—we have established that N cannot have negative eigenvalues. We must eventually reach a state a annihilates the state. (At each step down, a annihilates one quantum of energy—so a is often called an annihilation or destruction operator.)

Since the norm squared of , and > 0 for any nonvanishing state, it must be that the lowest eigenstate, the has n = 0. It follows that the n’s on the ladder are the positive integers, so from this point we relabel the eigenstates with n in place of n.

It is important to appreciate that we have, using Dirac’s factorization trick and with very little effort, found all the eigenvalues of the Hamiltonian

Contrast the work needed in this section with that in the standard Schrödinger approach. We have also established that the lowest energy state |0> must satisfy the first-order differential equation , that is,

The solution, unnormalized, is

(In fact, we’ve seen this equation and its solution before: this was the condition for the “least uncertain” wave function in the discussion of the Generalized Uncertainty Principle.)

We denote the normalized set of eigenstates Now and C_n is easily found:

and

Therefore, if we take the set of orthonormal states as the basis in the Hilbert space, the only nonzero matrix elements of are That is to say,

(The column vectors in the space this matrix operates on have an infinite number of elements: the lowest energy, the ground state component, is the entry at the top of the infinite vector—so up the energy ladder is down the vector!)

The adjoint

So

For practical computations, we need to find the matrix elements of the position and momentum variables between the normalized eigenstates. Now

so

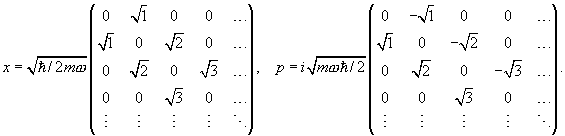
These matrices are, of course, Hermitian (not forgetting the i factor in p).

To find the matrix elements between eigenstates of any product of x’s and p’s, express all the x’s and p’s in terms of a’s and ’s, to give a sum of products of a’s and ’s. Each product in this sum can be evaluated sequentially from the right, because each a or has only one nonzero matrix element when the product operates on one eigenstate.

Normalizing the Eigenstates in x-space

The normalized ground state wave function is

where we have gone back to the original x variable and normalized with the standard Gaussian result.

To find the normalized wave functions for the higher states, we first construct them using the creation operator acting on the ground state |0>, then write as a differential operator, acting on the ground state wave function given above.

Using

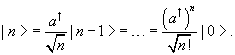
Inserting

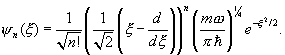
We must now establish that this expression is the same as the Hermite polynomial wave function derived earlier, and to do that we need some further properties of the Hermite polynomials.

Hermite Polynomials

The Hermite polynomials are defined by

so

It follows immediately from the definition that the coefficient of the leading power is 2ⁿ.

It is a straightforward exercise to check that H_n is a solution of the differential equation

so these are indeed the same polynomials we found by the series solution of Schrödinger’s equation earlier.

We can transform y_n(x) (from the end of the previous section) into this form by using the operator identity:

so

and

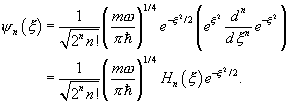
This established the equivalence of the two approaches to Schrödinger’s equation for the simple harmonic oscillator, and provides us with the overall normalization constants without doing cumbersome integrals.