Physics 751 Homework #9

1.

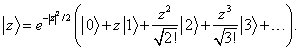
Exercise: Check that this state is correctly normalized, and is an eigenstate of .

2. Prove using an algebraic identity that is an eigenstate of . Is it also an eigenstate of ? Prove your assertion.

2. Prove that if ,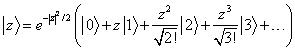

the unit operator

3. Prove that is correct up to terms A³ and B³ by expanding the exponentials on both sides and comparing.

4. How does a (position) translation operator affect a wave function expressed in momentum space, ? What is the operator that shifts the momentum space wave function to ? How does that operator change ?

5. Prove:

by writing the Taylor series for and finding the successive derivatives at the origin.

A unitary squeeze operator is defined by:

Use the result for above to prove that:

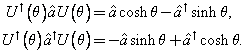
Deduce that

so for positive θ, the wave function is scaled down—squeezed—in x space, but simultaneously expanded in p space, as it must be, since it was a minimum uncertainty packet.

Is it still a minimum uncertainty packet? Is it still an eigenstate of the annihilation operator? If not, what is it an eigenstate of? How do you think it develops in time?