Physics 751 Final Exam
December 2002
This exam is to be pledged: write the pledge at the
top of your first sheet, and sign it.
Do five questions, and make clear which question you
do not want counted if you attempted six.
Otherwise, I will just grade the first five.
Possibly Useful Info:
Laplacian in Spherical Polars:
![]()
For the one-dimensional oscillator the operator a:
![]()
Angular Momentum Operators:
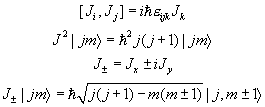
Electron mass = 10-27grams, charge = 1.6´10-19coul
= 4.8´10-10
esu, ![]() = 10-34
SI, =10-27 cgs.
= 10-34
SI, =10-27 cgs.
Questions:
1. (a) Find the energy of the bound state of a single attractive delta function potential ld(x) at the origin in one dimension.
(b) Suppose now the attractive potential is ld(x-a), with a greater than zero, but there is also an infinitely high repulsive wall at x = 0. Find now under what conditions the delta function has a bound state, and find an equation for the bound state energy.
(c) Establish that in the limit of large a, your result from (b) tends to that from (a). (continued)
(d) State in a couple of sentences or so how your results in (b) would be qualitatively changed if the repulsive wall at x = 0 were only of finite height.
2. A beam
of spin-1 particles, moving along the y axis, is incident on two
collinear SG apparatuses, the first with B along the z axis, and the
second with B along the z¢ axis, which lies in the x-z
plane at an angle q
relative to the z axis. Both apparatuses transmit only the
uppermost beams. What fraction leaving the first will pass the second?
3. What
are the possible values of total angular momentum if a spin 3/2 is combined
with a spin one? Work out explicitly
all possible (normalized) spin wavefunctions having total angular momentum in
the z-direction greater than zero.
4. (a)
Assuming p, x obey canonical commutation relations, find the
commutation relations for the simple harmonic oscillator raising and lowering
operators (see formulas at beginning of exam).
Generalize your result to find ![]() (First take n
= 2, then n = 3, and look for the pattern).
(First take n
= 2, then n = 3, and look for the pattern).
(b) Prove
that ![]() is an eigenstate of
the (non-Hermitian) annihilation operator a. Find its eigenvalue, and normalize it. Is l necessarily real?
is an eigenstate of
the (non-Hermitian) annihilation operator a. Find its eigenvalue, and normalize it. Is l necessarily real?
5. (a) An
electron is in the ground state in a spherically symmetric potential equal to
zero for r less than a, and infinity for r greater than or
equal to a. Find the energy of the electron.
(b)
Suppose now the electron is in a spherical well V = -V0 for r
less than a, V = 0 otherwise. The electron is in the lowest
state, which is just bound (total energy very close to zero). How does V0 depend on a?
(c) Using
(b), estimate whether a large nucleus (like uranium) could have an electron
bound mainly inside the nucleus.
6. A
one-dimensional box has length 2L and starts out with an impermeable
partition in its middle, so it is really two independent boxes of length L.
A particle starts out in the ground state of the left-hand box. At t =
0, without disturbing the wavefunction, the partition is instantaneously
removed. The wavefunction then evolves
in time in the bigger box. A time t later, the energy of the particle in
the big box is measured. What are the possible values of this measurement, and
what is the probability of each?