Coherent States of the Simple Harmonic Oscillator
Michael Fowler, 1/24/06
What is the Wave Function of a Swinging Pendulum?
Consider a macroscopic simple harmonic oscillator, and to keep things simple assume there are no interactions with the rest of the universe. We know how to describe the motion using classical mechanics: for a given initial position and momentum, classical mechanics correctly predicts the future path, as confirmed by experiments with real (admittedly not perfect) systems. But from the Hamiltonian we could also write down Schrödinger’s equation, and from that predict the future behavior of the system. Since we already know the answer from classical mechanics and experiment, quantum mechanics must give us the same result in the limiting case of a large system.
It is a worthwhile exercise to see just how this happens. Evidently, we cannot simply follow the classical method of specifying the initial position and momentum—the uncertainty principle won’t allow it. What we can do, though, is to take an initial state in which the position and momentum are specified as precisely as possible. Such a state is called a minimum uncertainty state (the details can be found in my earlier lecture on the Generalized Uncertainty Principle).
In fact, the ground state of a simple harmonic oscillator is a minimum uncertainty state. This is not too surprising—it’s just a localized wave packet centered at the origin. The system is as close to rest as possible, having only zero-point motion. What is surprising is that there are excited states of the pendulum in which this ground state wave packet swings backwards and forwards indefinitely, a quantum realization of the classical system, and the wave packet is always one of minimum uncertainty. Recall that this doesn’t happen for a free particle on a line—in that case, an initial minimal uncertainty wave packet spreads out because the different momentum components move at different speeds. But for the oscillator, the potential somehow keeps the wave packet together, a minimum uncertainty wave packet at all times. These remarkable quasi-classical states are called coherent states, and were discovered by Schrodinger himself. They are important in many quasi-classical contexts, including laser radiation.
Our task here is to construct and analyze these coherent states and to find how they relate to the usual energy eigenstates of the oscillator.
Classical Mechanics of the Simple Harmonic Oscillator
To define the notation, let us briefly recap the dynamics of the classical oscillator: the constant energy is
![]()
or
![]() .
.
The classical motion is most simply described in phase space, a two-dimensional plot in
the variables ![]() . In this space, the point
. In this space, the point
![]() corresponding to the
position and momentum of the oscillator at an instant of time moves as time
progresses at constant angular speed w
in a clockwise direction around the circle of radius
corresponding to the
position and momentum of the oscillator at an instant of time moves as time
progresses at constant angular speed w
in a clockwise direction around the circle of radius ![]() centered at the origin.
centered at the origin.
This motion is elegantly described by regarding the two-dimensional phase space as a complex plane, and defining the dimensionless complex variable
![]() .
.
The time evolution in phase space is simply ![]() .
.
The particular choice of (quantum!) scaling factor in
defining z amounts to defining the
unit of energy as ![]() , the natural unit for the oscillator: it is easy to check that if the classical
energy
, the natural unit for the oscillator: it is easy to check that if the classical
energy ![]() then the dimensionless
then the dimensionless
![]() is simply the number
is simply the number ![]() (which is of course
very large, so the ½ is insignificant).
(which is of course
very large, so the ½ is insignificant).
Minimum Uncertainty Wave Packets
We established in the lecture on the Generalized Uncertainty
Principle that any minimum uncertainty one-dimensional wave function (so ![]() ) for a particle must satisfy the linear differential
equation (here
) for a particle must satisfy the linear differential
equation (here ![]() )
)
![]()
where ![]() , l
are constants, and l is pure imaginary. The equation
is easy to solve: any minimum uncertainly one-dimensional wave function is a
Gaussian wave packet, having expectation value of momentum
, l
are constants, and l is pure imaginary. The equation
is easy to solve: any minimum uncertainly one-dimensional wave function is a
Gaussian wave packet, having expectation value of momentum ![]() , centered at
, centered at ![]() and having width
and having width ![]() . (Dx is defined for a state
. (Dx is defined for a state ![]() by
by ![]() .)
.)
That is to say, the minimum uncertainly solution is:
![]()
with C the normalization constant.
In fact, the simple harmonic oscillator ground state ![]() is just such a minimum
uncertainty state, with
is just such a minimum
uncertainty state, with
![]() .
.
Furthermore, it is easy to see that the displaced ground state ![]() (writing the normalization constant
(writing the normalization constant ![]() ) must also be a minimum uncertainty state, with the same
) must also be a minimum uncertainty state, with the same ![]() . Of course, in
contrast to the ground state, this displaced state is no longer an eigenstate
of the Hamiltonian, and any such initial state will change with time.
. Of course, in
contrast to the ground state, this displaced state is no longer an eigenstate
of the Hamiltonian, and any such initial state will change with time.
(Both these states have the same spread in x-space ![]() , and the same spread in p-space,
the only difference in the p
direction being a phase factor
, and the same spread in p-space,
the only difference in the p
direction being a phase factor ![]() for the displaced state.)
for the displaced state.)
What about the higher eigenstates of the oscillator Hamiltonian?
They are not minimally uncertain
states—for the nth state, ![]() , as is easily checked using
, as is easily checked using ![]() . So, if we construct a
minimally uncertain higher energy state, it will not be an eigenstate of the Hamiltonian.
. So, if we construct a
minimally uncertain higher energy state, it will not be an eigenstate of the Hamiltonian.
Exercise: prove ![]() for the nth energy eigenstate. (Hint:
use creation and annihilation operators.)
for the nth energy eigenstate. (Hint:
use creation and annihilation operators.)
Time Development of a Coherent State: the Role of the Annihilation Operator
In this section, we shall establish a remarkable connection between minimally uncertain oscillator states and the annihilation operator, then use properties of that oscillator to find the time-development of the minimally uncertain states.
Suppose that at t = 0 the oscillator wave function is the minimum uncertainty state
![]()
centered at ![]() in phase space (as
defined above for the classical oscillator), and with
in phase space (as
defined above for the classical oscillator), and with ![]() to give it the same spatial extent as the ground state.
to give it the same spatial extent as the ground state.
From the preceding section, this![]() satisfies the minimum uncertainty equation
satisfies the minimum uncertainty equation
![]()
Rearranging this equation shows it in a different light:
![]() .
.
This is an eigenvalue equation! The wave packet ![]() is an eigenstate of
the operator
is an eigenstate of
the operator ![]() with eigenvalue
with eigenvalue ![]() . It is not, of course, an eigenstates of either
. It is not, of course, an eigenstates of either
![]() or
or ![]() taken individually.
taken individually.
Furthermore, the
operator ![]() is just a constant
times the annihilation operator
is just a constant
times the annihilation operator ![]() --recall
--recall
![]()
Therefore, this minimally uncertain initial wave packet ![]() is an eigenstate of
the annihilation operator
is an eigenstate of
the annihilation operator ![]() , with eigenvalue
, with eigenvalue ![]() . By the way, it’s ok
for
. By the way, it’s ok
for ![]() to have complex
eigenvalues, because
to have complex
eigenvalues, because ![]() is not a hermitian
operator.
is not a hermitian
operator.
We can now make the connection with the complex plane
representation of the classical operator: the eigenvalue ![]() is precisely the
dimensionless complex parameter
is precisely the
dimensionless complex parameter![]() !
!
This means that if we have a minimal uncertainty oscillator wave packet
![]()
having the same spatial extent as the ground state, centered
at ![]() in phase space, and we
write
in phase space, and we
write
![]()
Then
![]() .
.
That is to say, all
eigenstates of the annihilation operator![]() are minimal uncertainty wave packets having the same spatial
width as the oscillator ground state.
are minimal uncertainty wave packets having the same spatial
width as the oscillator ground state.
Turning now to the time development of the state, it is convenient to use the ket notation
![]()
so as usual
![]() .
.
We shall show that ![]() remains an eigenstate of the annihilation operator for all times t: it therefore continues to
be a minimum uncertainty wave packet!
remains an eigenstate of the annihilation operator for all times t: it therefore continues to
be a minimum uncertainty wave packet!
The key point in establishing this is that the annihilation operator itself has a simple time development in the Heisenberg representation,
![]() .
.
To prove this, consider the matrix elements of ![]() between any two eigenstates
between any two eigenstates ![]() of the Hamiltonian
of the Hamiltonian
![]()
so
![]() .
.
Since the only nonzero matrix elements of the annihilation
operator ![]() are for
are for ![]() , and the energy eigenstates form a complete set, this simple
time dependence is true as an operator
equation
, and the energy eigenstates form a complete set, this simple
time dependence is true as an operator
equation
![]() .
.
It is now easy to prove that ![]() is always an
eigenstate of
is always an
eigenstate of ![]() :
:
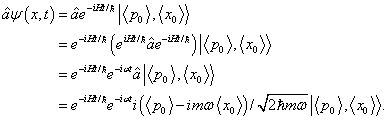
Therefore the annihilation operator, which at t = 0 had the eigenvalue ![]() , corresponding to a minimal wave packet centered at
, corresponding to a minimal wave packet centered at ![]() in phase space, evolves
in time t to another minimal packet
(because it’s still an eigenstate of the annihilation operator), and writing
in phase space, evolves
in time t to another minimal packet
(because it’s still an eigenstate of the annihilation operator), and writing
![]() ,
,
the new eigenvalue
![]()
or more succinctly
![]() .
.
Therefore, the center of the minimal wave packet in phase space follows the classical path in time. This is made explicit by equating real and imaginary parts:
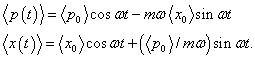
So we’ve found Schrödinger’s “best possible” quantum description of a classical oscillator.
The Translation Operator
It’s worth repeating the exercise for the simple case of the
oscillator initially at rest a distance ![]() from the center. This gives a neat tie-in with the translation
operator.
from the center. This gives a neat tie-in with the translation
operator.
Let us then take the initial state to be ![]() where
where ![]() is the ground state
wave function—so we’ve moved the packet to the right by
is the ground state
wave function—so we’ve moved the packet to the right by![]() .
.
From the ![]() to be the variable!)
to be the variable!)
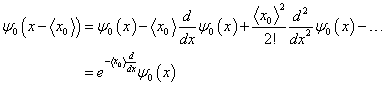
Evidently the translation
operator ![]() shifts the wave function a distance
shifts the wave function a distance ![]() to the right.
to the right.
Since ![]() , the translation operator can also be written as
, the translation operator can also be written as![]() , and from this it can be expressed in terms of
, and from this it can be expressed in terms of ![]() , since
, since
![]() , so
, so ![]() ,
,
![]() being Hermitian, and
being Hermitian, and
![]() .
.
Therefore the displaced ground state wave function can be written
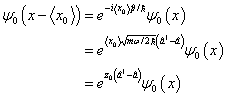
for real ![]() , since
, since ![]() is zero for this
initial state (the wave function is real).
is zero for this
initial state (the wave function is real).
How do we generalize this translation operator to an
arbitrary state, with nonzero ![]() ? Thinking in terms of the complex parameter space z, we need to be able to move in both
the x and the p directions, using both
? Thinking in terms of the complex parameter space z, we need to be able to move in both
the x and the p directions, using both ![]() and
and ![]() . This is slightly
tricky since these operators do not commute, but their commutator is just a
number, so (using a theorem from the Appendix) this will only affect the
overall normalization.
. This is slightly
tricky since these operators do not commute, but their commutator is just a
number, so (using a theorem from the Appendix) this will only affect the
overall normalization.
Furthermore, both ![]() and
and ![]() are combinations of
are combinations of ![]() , so the generalization of
, so the generalization of ![]() from real
from real ![]() to complex z,
to be unitary, must have an antihermitian combination of
to complex z,
to be unitary, must have an antihermitian combination of ![]() in the exponent—a unitary operator has the form
in the exponent—a unitary operator has the form ![]() , where H is Hermitian,
so iH is antihermitian..
, where H is Hermitian,
so iH is antihermitian..
We are led to the conclusion that
![]() ,
,
conveniently labeling the coherent state using the complex parameter z of its center in phase space. Since the generalized translation operator is unitary, the new state is correctly normalized.
This equation suggests the possibility of representing the
displaced state ![]() in the standard energy
basis
in the standard energy
basis ![]() . Expanding the
exponential yields an infinite series of terms
. Expanding the
exponential yields an infinite series of terms ![]() . These could then be
evaluated—in principle. It turns out not
to be such a good idea—since
. These could then be
evaluated—in principle. It turns out not
to be such a good idea—since ![]() don’t commute, the higher order terms become intractable.
don’t commute, the higher order terms become intractable.
Fortunately, the problem is easily solved using the operator
identity ![]() , true for operators A
and B provided
, true for operators A
and B provided ![]() commutes with A and B. (See the Appendix for a
proof.)
commutes with A and B. (See the Appendix for a
proof.)
Using this identity with ![]()
![]()
where we have used ![]() since
since ![]() .
.
It is now straightforward to expand the exponential:
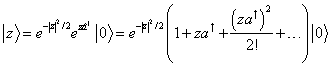
and recalling that the normalized energy eigenstates are

we find

Exercise: Check that this state is correctly
normalized, and is an eigenstates of ![]() .
.
Time Development of an Eigenstate of a Using the Energy Basis
Now that we have expressed the eigenstate ![]() as a sum over the
eigenstates
as a sum over the
eigenstates ![]() of the Hamiltonian,
finding its time development in this representation is straightforward: since
of the Hamiltonian,
finding its time development in this representation is straightforward: since ![]() ,
,
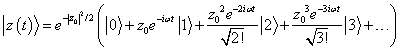
which can be written
![]()
equivalent to the result ![]() derived earlier.
derived earlier.
Some Properties of the Set of Eigenstates of a
In quantum mechanics, any physical variable is represented by a Hermitian operator. The eigenvalues are real, the eigenstates are orthogonal (or can be chosen to be so for degenerate states) and the eigenstates for a complete set, spanning the space, so any vector in the space can be represented in a unique way as a sum over these states.
The operator ![]() is not Hermitian. Its eigenvalues are all the numbers in the complex plane. The eigenstates belonging to different
eigenvalues are never orthogonal, as is immediately obvious on considering the
ground state and a displaced ground state.
The overlap does of course decrease rapidly for states far away in phase
space.
is not Hermitian. Its eigenvalues are all the numbers in the complex plane. The eigenstates belonging to different
eigenvalues are never orthogonal, as is immediately obvious on considering the
ground state and a displaced ground state.
The overlap does of course decrease rapidly for states far away in phase
space.
The state overlap can be computed using ![]() :
:
![]()
And we can then switch the operators ![]() using the theorem from the Appendix
using the theorem from the Appendix ![]() , leaving
, leaving ![]() and
and
![]() .
.
Finally, using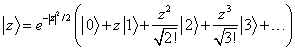 , we can construct a
unit operator using the
, we can construct a
unit operator using the ![]() ,
,
![]()
Where the integral is over the whole complex plane ![]() (this x is not, of course, the original
position x). Therefore, the
(this x is not, of course, the original
position x). Therefore, the ![]() span the whole space.
span the whole space.
Appendix: Some Exponential Operator Algebra
Suppose that the commutator of two operators A, B
![]()
where c commutes
with A and B, usually it’s just a number, for instance 1 or ![]() .
.
Then

That is to say, the commutator of A with elB is proportional to elB itself.
That is reminiscent of the simple harmonic oscillator
commutation relation ![]() which led directly to
the ladder of eigenvalues of H separated by
which led directly to
the ladder of eigenvalues of H separated by ![]() . Will there be a
similar “ladder” of eigenstates of A in general?
. Will there be a
similar “ladder” of eigenstates of A in general?
Assuming A (which is a general operator) has an
eigenstate ![]() with eigenvalue a,
with eigenvalue a,
![]()
Applying![]() to the eigenstate
to the eigenstate ![]() :
:
![]()
Therefore, unless it is identically zero, ![]() is also an eigenstate of A, with eigenvalue a
+ lc.
We conclude that instead of a ladder of eigenstates, we can apparently generate
a whole continuum of eigenstates, since l can be set
arbitrarily!
is also an eigenstate of A, with eigenvalue a
+ lc.
We conclude that instead of a ladder of eigenstates, we can apparently generate
a whole continuum of eigenstates, since l can be set
arbitrarily!
To find more operator identities, premultiply ![]() by e-lB
to find:
by e-lB
to find:
![]()
This identity is only true for operators A, B whose commutator c is a number. (Well, c could be an operator, provided it still commutes with both A and B).
Our next task is to establish the following very handy identity, which is also only true if [A,B] commutes with A and B:
![]()
The proof (due to Glauber, given in Messiah) is as follows:
Take ![]()
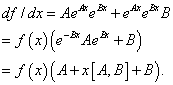
It is easy to check that the solution to this first-order differential equation equal to one at x = 0 is
![]()
so taking x = 1 gives the required identity, ![]()
It also follows that ![]() provided—as
always—that [A, B] commutes with A and B.
provided—as
always—that [A, B] commutes with A and B.