Note on Degenerate Second Order Perturbation Theory
Michael Fowler
(This note addresses problem 5.12 in Sakurai, taken from problem 7.4 in Schiff. A three state system has two of its levels degenerate in energy in zeroth order, but the perturbation has zero matrix element between these degenerate levels, so any lifting of the degeneracy must be by higher order terms.)
Hamiltonian 
Full Hamiltonian in this basis: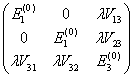 
More or less following Schiff page 157(Second Edition), but
in different notation, we will denote the eigenstates
of the full Hamiltonian correct to second
order in l
by
etc.
We do not know at this point the zero order kets in the degenerate subspace, so the correct-to-second-order kets have the form:
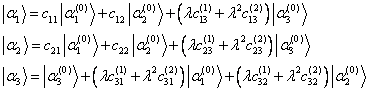
We write the eigenenergy correct
to second order as: 
.
Now for the first ket 
, that is,
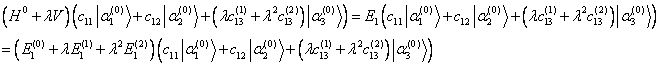
Taking the inner product of this equation with
, the zeroth-order term is just the
trivial 
, the first-order term in l
gives 
, in our case this is zero since we have no diagonal terms in
the interaction.
The second-order term in l gives:
Now we take the inner product with 
, and find to first-order in l:
or
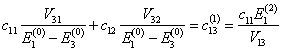
finally
Taking now the inner product of the eigenvalue
equation with 
gives for the
second-order term
So the identical argument leads to
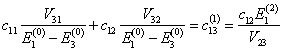
and
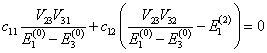
together with
We find the two possible values for 
by setting the
determinant to zero.
For the Sakurai-Schiff example, 
To switch to their
notation at this point, we write 
.
The determinant becomes (switching the rows):
.
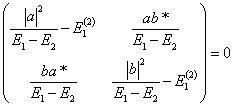The quadratic equation for is thus
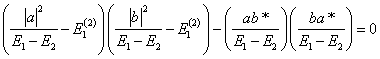
or
with roots
