Physics 752 Final Review Sheet
May 2004
Topics to Review
Tip: look over all
the homework questions.
1. Charged particle in a
magnetic field: know the Hamiltonian 
and how to solve the
corresponding Schrödinger equation for an electron in a plane with a uniform perpendicular magnetic field. Know the relation between canonical momenta
and velocities, and be able to count states of a given energy per unit area.
2. Path Integrals: know the definition of the propagator as a sum over paths
Understand the connection between the classical limit of this expression and the classical path. Be able to establish that this propagator satisfies Schrödinger’s equation for a particle in one dimension in a potential.
3. Spherical Tensors: read
my web notes, or equivalent. Know by
heart the components of a spherical vector,
and be sure you thoroughly understand the Wigner-Eckart
theorem, and in particular what selection rules it implies.
4. Variational Methods: know how to find an upper limit on the ground state energy using a Gaussian or other simple trial function, for any simple potential, both in one dimension and for spherically symmetric potentials in three dimensions. Have some idea how to find the next excited state for a symmetric potential in one dimension.
5. WKB: know the formula
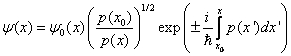
and when it is valid—be able to give a physical interpretation of the terms. Know how to use it to estimate tunneling amplitudes, and know how the results of the connection formulas lead to the quantization rule (which you should also know—and when it’s valid)
Know the corresponding formula for spherically symmetric wavefunctions.
6. Time-Independent Perturbation Theory: know by heart (but also know how to derive!) the first- and second-order terms:
Be familiar with the Selection Rules: Parity and Wigner-Eckart Theorem.
Degenerate Perturbation Theory: understand the essential point that you have to diagonalize the perturbation H 1 in the subspace of degenerate states of H 0, and be prepared to do it in a simple case. In particular, know how to find a diagonal basis for spin-orbit coupling. Read my on-line notes on the Peierls Transition, a good example of degenerate perturbation theory.
7. Time-Dependent Perturbation Theory: know by heart (but also know how to derive!) the first-order term:
You should be able to use this to find transition probabilities in a system when an external potential acts over some time period, and know when this is a valid approximation.
Know the routine for handling a sudden perturbation, and when it is valid to apply it (how sudden is sudden?).
Similarly for an adiabatic approximation: when is that ok?
8. The Periodic Perturbation: most important! Understand the derivation of Fermi’s Golden Rule, and know the rule by heart. And, know how to handle the delta function in applying the rule in actual computation.
You can skip Shankar’s section 18.3 on higher orders, but read my web notes instead.
9. Classical Electrodynamics: you should understand how a gauge transformation of the magnetic field also means changing the phase of an electron wave function, and this can happen even if the electron stays in a region where there is zero magnetic field. You should be familiar with the vector potential formulation of an electromagnetic wave, how the vector potential is related to the magnetic and the electric fields in a wave, and the polarization.
10. Read carefully the whole section on the Photoelectric Effect in hydrogen.
11. The Quantized Radiation Field and
Spontaneous Emission:
Review the relevant sections in Chapter 2 of Sakurai. In particular, understand how he arrives at the expression for the quantized vector potential in a wave, (2.60),
where the a’s are standard simple harmonic oscillator type annihilation and creation operators. Then skip forward to section 2-4, and read it as far as equation (2.140). That is to say, review spontaneous emission in the dipole approximation.