1) The virtual photon exchanged in the
Level 1
1) The virtual photon exchanged in the ![]() scattering diagram
discussed in class is space-like. Explain what this means and give an
example of a similar process involving a time-like exchange.
scattering diagram
discussed in class is space-like. Explain what this means and give an
example of a similar process involving a time-like exchange.
2) Show that for an electron at Jlab energies (![]() ), its mass
can be disregarded in writing the energy-momentum relation. What percentage
error would one have if muons (
), its mass
can be disregarded in writing the energy-momentum relation. What percentage
error would one have if muons (![]() ) were considered?
How long does it take an electron to travel the length of one linac
track
) were considered?
How long does it take an electron to travel the length of one linac
track ![]() mile? How long would a muon take?
mile? How long would a muon take?
(the values of the particles' masses in multiple of the ![]() units,
can be found on the PDG data group
website).
units,
can be found on the PDG data group
website).
3) Consider the nuclear reaction:
where ![]() represents the deuteron, and
represents the deuteron, and ![]() the neutron. If the energy
the neutron. If the energy
![]() MeV is released, what is the difference between the combined
initial masses, and the combined masses of
MeV is released, what is the difference between the combined
initial masses, and the combined masses of ![]() and the neutron?
and the neutron?
4) Two events happen in a particle accelerator at a distance of
![]() m, and separated in time by
m, and separated in time by
![]() s. What
are the distance and time between the events as seen in the frame
of a proton moving at
s. What
are the distance and time between the events as seen in the frame
of a proton moving at ![]() along a line between the two.
along a line between the two.
5) Making use of the anticommutation relation of the gamma matrices show that:
![]() .
.
Level 2
1) By using Dirac's Equation and its conjugate, demonstrate that
the covariant flux density is:
![]() .
.
2) Demonstrate that: (a) the angular momentum,
![]() ,
,
and (b) the total angular momentum,
![]() with:
with:
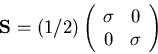
are conserved.
3) Show that:
with
![]() .
.
4) By showing that
![]() ,
demonstrate that the matrix:
,
demonstrate that the matrix:
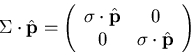
where
![]() , commutes with the free
particle Hamiltonian,
, commutes with the free
particle Hamiltonian, ![]() (
(
![]() is the particle's helicity).
is the particle's helicity).