DEFINITIONS AND REVIEW OF CURRENT DATA

The Gerasimov-Drell-Hern (GDH) sum rule is of fundamental importance to our understanding of the nucleon. It is based on some very general principles of physics including Lorentz and Gauge invariance, cross symmetry, causality and unitarity thereby making it model independent. It's 1/ν weighting make the lower lying resonances most important. Additionally the connection between the GDH sum rule at low Q² and the Ellis-Jaffe sum rule in the deep inelastic region is of great interest.

The actual GDH sum rule was derived at Q²=0 (for real photons):

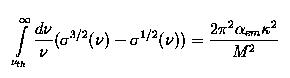
Where ν is the photon energy, ν_th is the photo-absorption threshold, M is the nucleon mass and σ_1/2 and σ_3/2 are the absorption cross sections for total helicity 1/2 and 3/2.

At Q² different from 0 one can define the polarized structure functions g₁ and g₂.

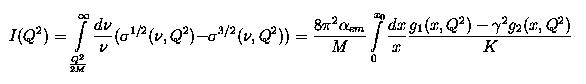
Here x₀=Q²/2Mν₀ and K is the flux factor of vitual photons &nu &radic 1+&gamma² , and γ² = Q ²/ ν². This reduces to the GDH sum rule for Q²=0.

In the DIS limit the integral becomes.

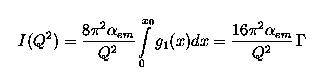
Here Γ is the first momentum of g₁.
Studying the GDH sum rule at various Q² allows us to investigate the question of the transition from the high Q² to the low Q² regimes. The change of signs that occurs in the region 0 < Q² < 1 GeV² is parcicularily puzzling.

PROTON AND NEUTRON DATA

There are 4 major Q² regions of interest.

High Q²
- Experimental Data
- Phenomenological Parametrizations
Intermediate Q²
- Experimental Data
  - Hermes data
  - e143 data
- Phenomenological Parametrizations
  - Burkert and Ioffe
  - Close et. al.
Low Q²
- Experimental Data
  - J-Lab data
- Phenomenological Parametrizations
  - Soffer and Teryaev
  - Bianchi and Thomas
Q² = 0
- Experimental Data
  - Mami

NEUTRON DATA

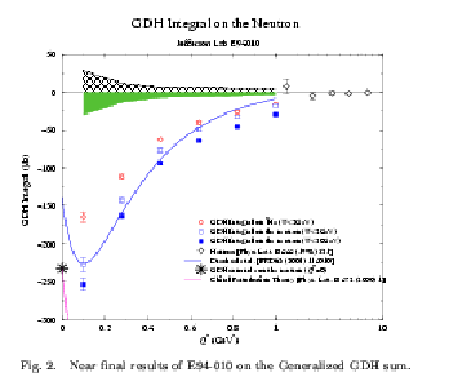
Jaideep's Data (Q² >0)
Recent data (Jlab, Hermes)

DISCUSSION (in progress ...)

An introduction to the GDH Sum Rule was first given by S.L.. We first discussed the meaning of the sum rule, the kinematical variables, their range and all that.
We came up with the material posted above.
The main issue is: the extended GDH sum rule, I(Q²) -- the sum rule at varying Q² -- is positive at large Q², because it is related to the first moment of g₁. On the other side, I(Q²=0) is negative . There must be a point where I(Q²) changes sign, or, in other words, I(Q²) does not extrapolate smoothly to the low Q² region, as predicted by pQCD, but a dramatic Q² dependence appears. The investigation of this point is of particular interest for understanding the transition between the perturbative and non-perturbative regimes of QCD.
A number of open questions remain:
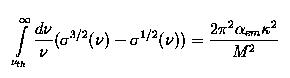
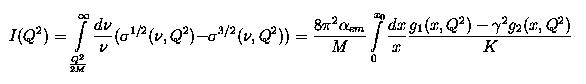
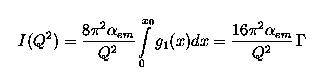
- list them!