1. Discovering Gravity

Michael Fowler

Terrestrial Gravity: Galileo Analyzes a Cannonball Trajectory

From the earliest times, gravity meant the tendency of most bodies to fall to earth. In contrast, things that leaped upwards, like flames of fire, were said to have “levity”. Aristotle was the first writer to attempt a quantitative description of falling motion: he wrote that an object fell at a constant speed, attained shortly after being released, and heavier things fell faster in proportion to their mass. Of course this is nonsense, but in his defense, falling motion is pretty fast—it’s hard to see the speed variation when you drop something to the ground. Aristotle most likely observed the slower motion of things falling through water, where buoyancy and fluid resistance dominate, and assumed that to be a slowed-down version of falling through air—which it isn’t.

Galileo was the first to get it right. (True, others had improved on Aristotle, but Galileo was the first to get the big picture.) He realized that a falling body picked up speed at a constant rate—in other words, it had constant acceleration (as he termed it, the word means “addition of speed” in Italian). He also made the crucial observation that, if air resistance and buoyancy can be neglected, all bodies fall with the same acceleration, bodies of different weights dropped together reach the ground at the same time. This was a revolutionary idea—as was his assertion that it should be checked by experiment rather than by the traditional method of trying to decipher what ancient authorities might have meant.

Galileo also noted that if a ball rolls without interference on a smooth horizontal surface, and friction and air resistance can be neglected, it will move with constant speed in a fixed direction—in modern language, its velocity remains constant.

He considered the motion of an object when not subject to interference as its “natural” motion.

Using his terminology, then, natural horizontal motion is motion at constant velocity, and natural vertical motion is falling at constant acceleration.

But he didn’t stop there—he took an important further step, which made him the first in history to derive useful quantitative results about motion, useful that is to his boss, a duke with military interests. The crucial step was the realization that for a cannonball in flight, the horizontal and vertical motions can be analyzed independently. Here’s his picture of the path of a horizontally fired cannonball animation here!):

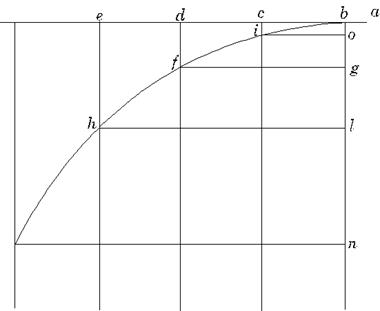
The vertical drop of the cannonball at the end of successive seconds, the lengths of the vertical lines ci, df, eh are the same vertical distances fallen by something dropped from rest. If you drop a cannonball over a cliff it will fall 5 meters in the first second, if you fire it exactly horizontally at 100 meters per second, it will still fall 5 meters below a horizontal line in the first second. Meanwhile, its horizontal motion will be at a steady speed (again neglecting air resistance), it will go 100 meters in the first second, another 100 meters in the next second, and so on. Vertically, it falls 5 meters in the first second, 20 meters total in two seconds, then 45 and so on.

Galileo drew the graph above of the cannonball’s position as a function of time, and proved the curve was parabolic. He went on to work out the range for given muzzle velocity and any angle of firing, much to the gratification of his employer.

Moving Up: Newton Puts the Cannon on a Very High Mountain

Newton asked the question: what if we put the cannon on a really high (imaginary, of course!) mountain above the atmosphere and fired the cannon really fast? The cannonball would still fall 5 meters in the first second (ignoring the minor point that g goes down a bit on a really high mountain), but if it’s going fast enough, don’t forget the curvature of the earth! The surface of the earth curves away below a horizontal line, so if we choose the right speed, after one second the cannonball will have reached a point where the earth’s surface itself has dropped away by 5 meters below the originally horizontal straight line. In that case, the cannonball won’t have lost any height at all—defining “height” as distance above the earth’s surface.

Furthermore, “vertically down” has turned around a bit (it means perpendicular to the earth’s surface) so the cannonball is still moving “horizontally”, meaning moving parallel to the earth’s surface directly beneath it. And, since it’s above the earth’s atmosphere, it won’t have lost any speed, so exactly the same thing happens in the next second, and the next—it therefore goes in a circular path. Newton had foreseen how a satellite would move—here’s his own drawing, with VD, VE and VF representing the paths of successively faster shots:

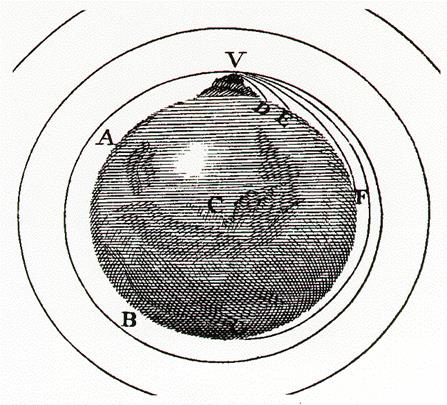
Newton’s brilliant insight—the above picture—is fully animated in my applet here.

We can find how fast the cannonball must move to maintain the circular orbit by using Pythagoras’ theorem in the diagram below (which grossly exaggerates the speed so that you can see how to do the proof).

The cannonball fired from point P goes $v$ meters horizontally in one second and drops 5 meters vertically, and, if $v$ has the right value, the cannonball will still be the same distance $R$ from the earth’s center it was at the beginning of the second. (Bear in mind that $v$ is actually about a thousandth of $R,$ so the change in the direction of “down” will be imperceptible, not like the exaggerated figure here.)

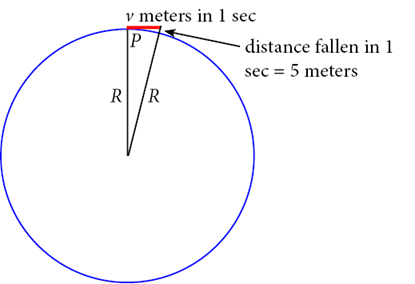
Knowing that the radius of the earth $R$ is 6400 km, there is enough information in the above diagram to fix the value of $v .$ Notice that there is a right angled triangle with sides $R$ and $v$ and hypoteneuse $R + 5.$

Applying Pythagoras’ theorem,

$\begin{array}{l} {(R + 5)}^{2} = R^{2} + v^{2}, \\ R^{2} + 10 R + 25 = R^{2} + v^{2} . \end{array}$

Newton knew (in different units) that $R$ = 6400 km, so the 25 in the above equation can be neglected to give:

$v^{2} = 10 R = 10 \times 6400 \times 1000, so v = 8000.$

The units for $v$ are of course meters per second, on our diagram we show $v$ as a distance, that traveled in the first second.

So the cannonball must move at 8 km per second, or 5 miles per second if its falling is to match the earth’s curvature—this is 18,000 mph, once round the earth in a little less than an hour and a half. This is in fact about right for a satellite in low earth orbit.

Onward into Space: The Cannonball and the Moon

It occurred to Newton one day (possibly because of a falling apple) that this familiar gravitational force we experience all the time here near the surface of the earth might extend outwards as far as the moon, and in fact might be the reason the moon is in a circular orbit. The radius of the moon’s orbit (384,000 km) and its speed in orbit (about 1 km per second) had long been known (see my notes here if you’re interested in how it was measured), so it was easy to find, using the same Pythagorean arguments as used for the cannonball above, that the moon “falls” 1.37 millimeters below a straight line trajectory in one second.

That is to say, the ratio of the moon’s acceleration towards the center of the earth to the cannonball’s is 1.37/5000, or about 1/3600.

But the radius of the moon’s orbit is about 60 times greater than the cannonball’s (which is just the radius of the earth, approximately). Since 60×60 = 3600, Newton concluded that the gravitational force decreased with distance as $1 / r^{2} .$

Newton’s Universal Law of Gravitation

Newton then boldly extrapolated from the earth, the apple and the moon to everything, asserting his Universal Law of Gravitation:

Every body in the universe attracts every other body with a gravitational force that decreases with distance as $1 / r^{2} .$

But actually he knew more about the gravitational force: from the fact that bodies of different masses near the earth’s surface accelerate downwards at the same rate, using $F = m a$ (his Second Law) if two bodies of different masses have the same acceleration they must be feeling forces in the same ratio as their masses (so a body twice as massive feels twice the gravitational force), that is, the gravitational force of attraction a body feels must be proportional to its mass.

Now suppose we are considering the gravitational attraction between two bodies (as we always are), one of mass $m_{1},$ one of mass $m_{2} .$ By Newton’s Third Law, the force body 1 feels from 2 is equal in magnitude (but of course opposite in direction) to that 2 feels from 1. If we think of $m_{1}$ as the earth, the force $m_{2}$ feels is proportional to $m_{2},$ as argued above—so this must be true whatever $m_{1}$ is. And, since the situation is perfectly symmetrical, the force must also be proportional to $m_{1} .$

Putting all this together, the magnitude of the gravitational force between two bodies of masses $m_{1}$ and $m_{2}$ a distance $r$ apart

$F = \frac{G m_{1} m_{2}}{r^{2}} .$

The constant $G$ = 6.67×10^-11 N.m²/kg².

It is important to realize that $G$ cannot be measured by any astronomical observations. For example, $g$ at the surface of the earth is given by

$g = \frac{G m_{E}}{r_{E}^{2}} .$

Here $m_{E}$ is the mass and $r_{E}$ the radius of the earth. Notice that by measuring $g,$ and knowing $r_{E},$ we can find $G m_{E} .$ But this does not tell us what $G$ is, since we don’t know $m_{E}$ ! It turns out that this same problem arises with every astronomical observation. Timing the planets around the Sun will give us $G m_{Sun} .$ So we can figure out the ratio of the Sun’s mass to the earth’s, but we can’t find an absolute value for either one.

The first measurement of $G$ was made in 1798 by Cavendish, a century after Newton’s work. Cavendish measured the tiny attractive force between lead spheres of known mass. For details on how an experiment at the University of Virginia in 1969 improved on Cavendish’s work, click on the UVa Physics site here.

Cavendish said he was “weighing the earth” because once $G$ was measured, he could immediately find the mass of the earth $m_{E}$ from $g = G m_{E} / r_{E}^{2},$ and then go on the find the mass of the Sun, etc.

Describing the Solar System: Kepler’s Laws

Newton’s first clue that gravitation between bodies fell as the inverse-square of the distance may have come from comparing a falling apple to the falling moon, but important support for his idea was provided by a detailed description of planetary orbits constructed half a century earlier by Johannes Kepler.

Kepler had inherited from Tycho Brahe a huge set of precise observations of planetary motions across the sky, spanning decades. Kepler himself spent eight years mathematically analyzing the observations of the motion of Mars, before realizing that Mars was moving in an elliptical path.

To appreciate fully how Kepler’s discovery confirmed Newton’s theory, it is worthwhile to review some basic properties of ellipses.

Mathematical Interlude: Ellipses 101

A circle can be defined as the set of all points which are the same distance $R$ from a given point, so a circle of radius 1 centered at the origin O is the set of all points distance 1 from O.

An ellipse can be defined as the set of all points such that the sum of the distances from two fixed points is a constant length (which must obviously be greater than the distance between the two points!). This is sometimes called the gardener’s definition: to set the outline of an elliptic flower bed in a lawn, a gardener would drive in two stakes, tie a loose rope between them, then pull the rope tight in all different directions to form the outline.

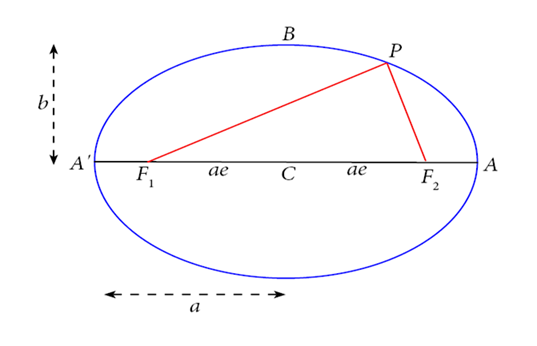
In the diagram, the stakes are at $F_{1}, F_{2}$ the red lines are the rope, $P$ is an arbitrary point on the ellipse.

$C A$ is called the semimajor axis length $a,$ $C B$ the semi-minor axis, length $b .$

$F_{1}, F_{2}$ are called the foci (plural of focus).

Notice first that the string has to be of length $2 a,$ because it must stretch along the major axis from $F_{1}$ to $A$ then back to $F_{2},$ and for that configuration there’s a double length of string along $F_{2} A$ and a single length from $F_{1}$ to $F_{2} .$ But the length $A^{'} F_{1}$ is the same as $F_{2} A,$ so the total length of string is the same as the total length $A^{'} A = 2 a .$

Suppose now we put $P$ at $B .$ Since $F_{1} B = B F_{2},$ and the string has length $2 a,$ the length $F_{1} B = a .$

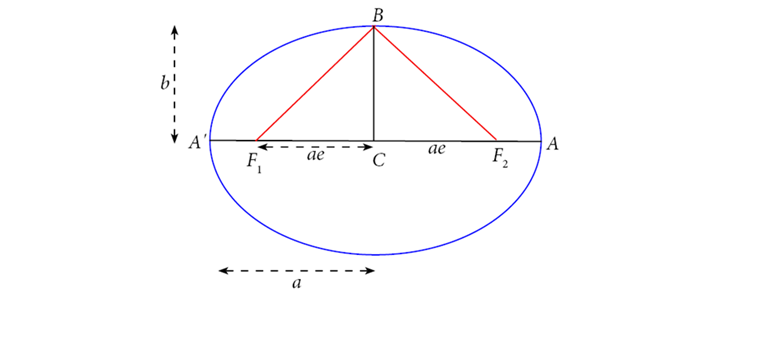
We get a useful result by applying Pythagoras’ theorem to the triangle $F_{1} B C,$

${(F_{1} C)}^{2} = a^{2} - b^{2} .$

(We shall use this shortly.)

Evidently, for a circle, $F_{1} C = 0.$

The eccentricity of the ellipse is defined as the ratio of $F_{1} C$ to $a,$ so

eccentricity $e = F_{1} C / a = \sqrt{1 - {(b / a)}^{2}} .$

The eccentricity of a circle is zero. The eccentricity of a long thin ellipse is just below one.

$F_{1}$ and $F_{2}$ on the diagram are called the foci of the ellipse (plural of focus) because if a point source of light is placed at $F_{1},$ and the ellipse is a mirror, it will reflect—and therefore focus—all the light to $F_{2} .$ (This can be proved using the string construction.)

An ellipse is essentially a circle scaled shorter in one direction: in $(x, y)$ coordinates it is described by the equation

$\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1,$

a circle being given by $a = b .$

In fact, in analyzing planetary motion, it is more natural to take the origin of coordinates at the center of the Sun rather than the center of the elliptical orbit. It is also more convenient to take $(r, θ)$ coordinates instead of $(x, y)$ coordinates, because the strength of the gravitational force depends only on $r .$ Therefore, the relevant equation describing a planetary orbit is the $(r, θ)$ equation with the origin at one focus. For an ellipse of semi major axis $a$ and eccentricity $e$ the equation is:

$\frac{a (1 - e^{2})}{r} = 1 + e \cos θ .$

It is not difficult to prove that this is equivalent to the traditional equation in terms of $x, y$ presented above.

Kepler summarized his findings about the solar system in his three laws:

1. The planets all move in elliptical orbits with the Sun at one focus.

2. As a planet moves in its orbit, the line from the center of the Sun to the center of the planet sweeps out equal areas in equal times, so if the area $S A B$ (with curved side $A B$ ) equals the area $S C D,$ the planet takes the same time to move from $A$ to $B$ as it does from $C$ to $D .$

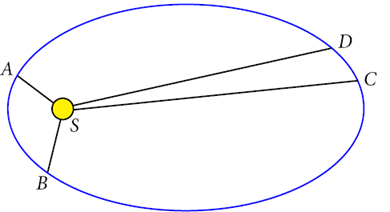
For my applet illustrating this law, click here.

3. The time it takes a planet to make one complete orbit around the Sun $T$ (one planet year) is related to its average distance from the Sun $R :$

$T^{2} \propto R^{3} .$

In other words, if a table is made of the length of year $T$ for each planet in the solar system, and its average distance from the Sun $R,$ and $T^{2} / R^{3}$ is computed for each planet, the numbers are all the same.

These laws of Kepler’s are precise, but they are only descriptive—Kepler did not understand why the planets should behave in this way. Newton’s great achievement was to prove that all this complicated behavior was the consequence of one simple law of attraction.

How Newton’s Law of Universal Gravitation Explains Kepler’s Laws

Surprisingly, the first of Kepler’s laws—that the planetary paths are elliptical—is the toughest to prove beginning with Newton’s assumption of inverse-square gravitation. Newton himself did it with an ingenious geometrical argument, famously difficult to follow. It can be more easily proved using calculus, but even this is nontrivial, and we shall not go through it in class. (The proof is given later in these notes, if you’re curious to see how it’s done.)

The best strategy turns out to be to attack the laws in reverse order.

Kepler’s Third Law (well, for circular orbits)

It is easy to show how Kepler’s Third Law follows from the inverse square law if we assume the planets move in perfect circles, which they almost do. The acceleration of a planet moving at speed $v$ in a circular orbit of radius $R$ is $v^{2} / R$ towards the center. (Of course you already know this, but it is amusing to see how easy it is to prove using the Pythagoras diagram above: just replace the 5 meters by $\frac{1}{2} a t^{2},$ the “horizontal” distance $v$ by $v t,$ write down Pythagoras’ theorem and take the limit of a very small time.)

Newton’s Second Law $F = m a$ for a planet in orbit becomes:

$\frac{m v^{2}}{R} = G \frac{M m}{R^{2}} .$

Now the time for one orbit is $T = 2 π R / v,$ so dividing both sides of the equation above by $R,$ we find:

${(\frac{T}{2 π})}^{2} = \frac{R^{3}}{G M}, so \frac{T^{2}}{R^{3}} = \frac{4 π^{2}}{G M} .$

This is Kepler’s Third Law: $T^{2} / R^{3}$ has the same numerical value for all the Sun’s planets.

Exercise: how are $R, T$ related if the gravitational force is proportional to $1 / R$ ? to $1 / R^{3}$ ? To $R$ ?

The point of the exercise is that Kepler’s Third Law, based on observation, forces us to the conclusion that the Law of Gravity is indeed inverse square.

In fact, Newton went further—he generalized the proof to elliptic orbits, and established that for the inverse square law the circle radius $R$ must (for ellipses) be replaced by $a,$ the semimajor axis of the ellipse, that is to say $T^{2} / a^{3}$ is the same for all planets. This is in fact exactly what Kepler found to be the case.

It follows immediately that all elliptic orbits with the same major axis length, whatever their eccentricity, have the same orbital time.

Kepler’s Second Law

A planet in its path around the Sun sweeps out equal areas in equal times.

Suppose at a given instant of time the planet is at point P in its orbit, moving with a velocity $\vec{v}$ meters per second in the direction along the tangent at P (see figure). In the next second it will move v meters, essentially along this line (the distance is of course greatly exaggerated in the figure) so the area swept out in that second is that of the triangle SPQ, where S is the center of the Sun.

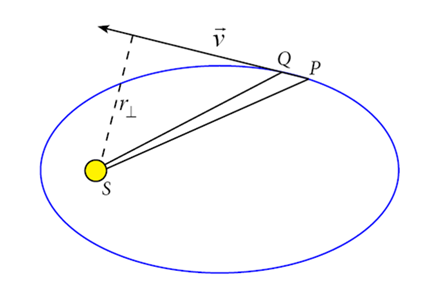
The area of triangle SPQ is just $½$ base × height. The base PQ is $v$ meters long, the height is the perpendicular distance $r_{⊥}$ from the vertex of the triangle at the Sun S to the baseline PQ, which is just the tangential velocity vector $\vec{v}$ .

Hence

rate of sweeping out of area = $\frac{1}{2} r_{⊥} v .$

Comparing this with the angular momentum $L$ of the planet as it moves around the Sun,

$L = m v r_{⊥}$

it becomes apparent that Kepler’s Second Law, the constancy of the area sweeping rate, is telling us that the angular momentum of the planet around the Sun is constant.

In fact,

rate of sweeping out of area = $\frac{L}{2 m} .$

To see what this constancy of angular momentum means, think of applying a force to a wheel on a fixed axle:

If the force is above the axle, as shown, the wheel will begin to turn anticlockwise; if it is below the axle the wheel will turn the other way—assuming no friction, the rate of change of angular momentum is equal to the torque, the product of the magnitude of the force and the perpendicular distance of the line of action of the force from the center of rotation, the axle. If the line of action of the force passes through the middle of the axle, there is no torque, no rotation, no change of angular momentum.

For the planet in orbit, the fact that the angular momentum about the Sun does not change means that the force acting on the planet has no torque around the Sun—the force is directly towards the Sun. This now seems obvious, but Kepler himself thought the planets were pushed around their orbits by spokes radiating out from the Sun. Newton realized that Kepler’s Second Law showed this was wrong—the force must be directly towards the Sun.

* Calculus Derivation of Kepler’s First Law

Note: I’m including this derivation of the elliptic orbit just so you can see that it’s calculus, not magic, that gives this result. This is an optional section, and will not appear on any exams.

We now back up to Kepler’s First Law: proof that the orbit is in fact an ellipse if the gravitational force is inverse square. As usual, we begin with Newton’s Second Law: $\vec{F} = m \vec{a},$ in vector form. The force is $G M m / r^{2}$ in a radial inward direction. But what is the radial acceleration? Is it just $d^{2} r / d t^{2} ?$ Well, no, because if the planet’s moving in a circular orbit it’s still accelerating inwards at $r ω^{2}$ (same as $v^{2} / r$ ) even though $r$ is not changing at all. The total acceleration is the sum, so $m \vec{a} = \vec{F}$ becomes:

$\frac{d^{2} r}{d t^{2}} - r ω^{2} = - \frac{G M}{r^{2}}$

This isn’t ready to integrate yet, because $ω$ varies too (in the elliptical case). But since the angular momentum $L$ is constant, and $L = m r^{2} ω,$ we can get rid of $ω$ in the equation to give:

$\frac{d^{2} r}{d t^{2}} = - \frac{G M}{r^{2}} + r {(\frac{L}{m r^{2}})}^{2} = - \frac{G M}{r^{2}} + \frac{L^{2}}{m^{2} r^{3}} .$

This equation can be integrated, using two very unobvious tricks, figured out by hindsight. The first is to change go from the variable $r$ to its inverse, $u = 1 / r .$ The other is to use the constancy of angular momentum to change the variable $t$ to $θ .$

Anyway,

$L = m r^{2} ω = \frac{m}{u^{2}} \frac{d θ}{d t}$

$\frac{d}{d t} = \frac{d θ}{d t} \frac{d}{d θ} = \frac{L u^{2}}{m} \frac{d}{d θ} .$

Therefore

$\frac{d r}{d t} = \frac{d}{d t} (\frac{1}{u}) = - \frac{1}{u^{2}} \frac{d u}{d t} = - \frac{L}{m} \frac{d u}{d θ}$

and similarly

$\frac{d^{2} r}{d t^{2}} = - \frac{L^{2} u^{2}}{m^{2}} \frac{d^{2} u}{d θ^{2}} .$

Substituting in the equation of motion gives:

$\frac{d^{2} u}{d θ^{2}} + u = \frac{G M m^{2}}{L^{2}}$

This equation is easy to solve! The solution is

$u = \frac{1}{r} = \frac{G M m^{2}}{L^{2}} + A \cos θ$

where $A$ is a constant of integration, determined by the initial conditions.

This is equivalent to the standard $(r, θ)$ equation of an ellipse of semi major axis $a$ and eccentricity $e,$ with the origin at one focus, which is:

$\frac{a (1 - e^{2})}{r} = 1 + e \cos θ .$

Deriving Kepler’s Third Law for Elliptical Orbits

The time it takes a planet to make one complete orbit around the Sun $T$ (one planet year) is related to the semi-major axis $a$ of its elliptic orbit by

$T^{2} \propto a^{3} .$

We have already shown how this can be proved for circular orbits, however, since we have gone to the trouble of deriving the $(r, θ)$ formula for an elliptic orbit, we add here the (optional) proof for that more general case.

(Note that this same result is derived in the next lecture using energy and angular momentum conservation—the proof given here is quicker, but depends on knowing the $(r, θ)$ equation for the ellipse.)

The area of an ellipse is $π a b,$ and the rate of sweeping out of area is $L / 2 m,$ so the time $T$ for a complete orbit is evidently

$T = \frac{π a b}{L / 2 m} .$

Putting the equation

$\frac{1}{r} = \frac{G M m^{2}}{L^{2}} + A \cos θ$

in the standard form

$\frac{a (1 - e^{2})}{r} = 1 + e \cos θ,$

we find

$L^{2} / G M m^{2} = a (1 - e^{2}) .$

Now, the top point $B$ of the semi-minor axis of the ellipse (see the diagram above) must be exactly $a$ from $F_{1}$ (visualize the string $F_{1} B F_{2}$ ), so using Pythagoras’ theorem for the triangle $F_{1} O B$ we find

$b^{2} = a^{2} (1 - e^{2}) .$

Using the two equations above, the square of the orbital time

$\begin{array}{l} T^{2} = {(2 m π a b)}^{2} / L^{2} \\ = {(2 m π a b)}^{2} / G M m^{2} a (1 - e^{2}) \\ = {(2 m π a b)}^{2} / G M m^{2} a (b^{2} / a^{2}) \\ = 4 π^{2} a^{3} / G M . \end{array}$

We have established, then, that the time for one orbit depends only on the semimajor axis of the orbit: it does not depend on how eccentric the orbit is.

index next PDF