A Brief Review of Nuclear Physics
Michael Fowler, University of Virginia
How Big is the Nucleus?
The relevant length scale for measuring nuclear size is the
femtometer 1 fm = 10-15 meters. Physicists usually call this length
one fermi. Nuclei vary from about one to a few fermis in
radius. Recall that the Bohr radius of
Hydrogen is of order 10-10 meters, so the nucleus is far smaller
than the atom. Nuclear size was first measured by
What is the Nucleus Made of?
The simplest nucleus, that of hydrogen, is a single proton: an elementary particle of mass about 940 MeV, carrying positive charge exactly opposite to the electron’s charge, having a spin of one half and being a fermion (so no two protons can be in the same quantum state).
The next simplest nucleus, called the deuteron, is a bound state of a proton and a neutron. The neutron, like the proton, is a spin one-half fermion, but it has no electric charge, and is slightly heavier (by 1.3 MeV) than the proton. The binding energy of the deuteron (analogous to the 13.6 eV for the Hydrogen atom) is 2.2MeV. A photon of this energy could “ionize” the deuteron into a separated proton and neutron. However, it is not necessary to actually do this experiment to establish how tightly the deuteron is bound. One need only weigh the deuteron accurately. It has a mass of 1875.61MeV. The proton has a mass of 938.27MeV, the neutron 939.56MeV, so together (but some distance apart!) they have a mass of 1877.93MeV, 2.2MeV more than the deuteron. Thus, when a proton and a neutron come together to form a deuteron, they must unload 2.2MeV of energy, which they do by emitting a photon (called a γ-ray at these energies).
Both protons and neutrons, being fermions, obey the exclusion principle, two protons with spin up cannot be in the same state, although two with opposite spin directions could, and a proton and a neutron can occupy the same spot at the same time!
Protons and neutrons are referred to as nucleons. The total number of nucleons in a nucleus is usually denoted by A, where A = Z + N, Z protons and N neutrons. The chemical properties of an atom are determined by the number of electrons, the same as the number of protons Z. This is called the atomic number. Nuclei can have the same atomic number, but different numbers of neutrons. These nuclei are called isotopes, the Greek for “same place”, since they are in the same place in the periodic table.
These nucleons attract each other with a short range but very strong force, called the nuclear force. The situation here is different from that for electrons in the atom, where the strong central force tends to dominate. In the nucleus the nucleons are attracted mainly by their immediate neighbors. Nevertheless, it is a useful beginning to think of this attractive force as being a potential well, as seen by an individual nucleon, and think in terms of the nuclei as filling the lowest available quantum states in this well, just as we did for electrons in the atom. We find, for example, that the Helium nucleus, 2p+2n, (a.k.a. the α-particle) is tightly boundthe four nucleons can all occupy the lowest state in the well. However, some larger nuclei, like C, O, Fe are actually a little more tightly bound even than He (about 8.5 MeV per nucleon as opposed to about 7.5 for He) because each nucleon is attracted to its close partners, and there are more close partners in these larger nuclei. It has also been argued that some of these higher nuclei strongly resemble bound states of α-particles. The total binding energy (usually expressed per nucleon) of any nucleus is easy to findjust as for the deuteron above, the mass of the nucleus is found accurately, and subtracted from the sum of the masses of the separate nucleons.
Coulomb Repulsion and α-decay
As one goes to really large nuclei, the binding per nucleon actually decreases. This is a consequence of the electrostatic repulsion between the protons. The essential point is that the Coulomb repulsion is long range, but the nuclear attraction is short range. Considering a proton at the surface of a nucleus, it is bound to the nucleus by the attractive forces of its nearest neighbors, say five or six of them, and this number is little affected as one goes up the periodic table from, say, Fe to U. On the other hand, the proton on the surface is being pushed away by the electrostatic repulsion from the other protons, and this increases substantially as the number of other protons goes from 25 in iron to 91 in uranium, even though they may be a little further away on average. In fact, this is why there is a limit on the size of atoms.
A large nucleus does not, however, tend to spit out protonsthere’s a much more economical way to unload charge. It ejects an α-particle. The binding energy of the nucleons in an α is almost exactly the same as it is in a U nucleus, so little nuclear binding has to be traded for lowering the electrostatic potential energy.
Thus the most common form of Uranium, U238 (A=238, Z=92) goes to Thorium (A=234, Z=90) by α-decay. The surprising thing is, it takes a time comparable to the age of the universe to do so! If it’s energetically desirable, why does it take so long?
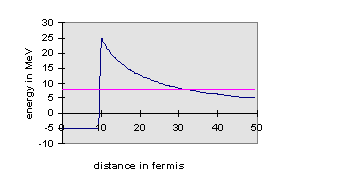
The answer is—there’s a barrier in the way. It is a good model to imagine the U to have the α particle inside it, confined to a deep square well potential representing the attractive nuclear force. However, the α-particle wavefunction will penetrate some distance into the wall of this finite square well potential, where the α will be away from the nuclear force, but not away from the long-range electrostatic repulsion of the other protons in the nucleus. The picture is, then, that outside the well, the ground is not flat—it’s like a well at the top of a hill. The implication of this is that if the energy level of the α inside the well is higher than the flat land surrounding the hill, the α-wavefunction after dying away underground as it tunnels out from the well will re-emerge at some distance, oscillating. In other words, there is some finite probability of finding the α shooting away from the nucleus some distance away. The actual probability of this happening depends on how much the wavefunction decayed as it tunneled underground away from the well, which depended on how far its energy was below the ground. For U238, this decay on tunneling away from the well is so rapid that the α takes on average billions of years to escape. However, many different nuclei undergo α-decay, the quickest in millionths of a second. The energies of the emitted α’s can be measured, and confirm this explanation of quantum mechanical tunneling, first put forward in 1928. The quickest decays correspond to the most energetic α’s, just as the tunneling picture would suggest.
β-decay
These heavier nuclei have more neutrons than protons, because the Coulomb repulsion makes it harder to bind protons. However, a price is paid—thinking of a shell-type model, the extra neutrons go into higher energy shells. Thus for nuclei of a given size, there is an optimum ratio of neutrons to protons, close to one for small nuclei where the Coulomb effects are small enough to be neglected, close to 1.5 for the largest nuclei.
Note that if a large nucleus decays by emitting an α, the nucleus left behind has an even greater ratio of neutrons to protons, since α = 2p+2n. This implies that it might be able to go to a lower energy state if it could trade a neutron for a proton. In fact, this can sometimes be done. The neutron itself is not a stable particle. A neutron alone in space will only last about ten minutes before ejecting an electron, leaving a proton behind. This is energetically possible, because the mass of the neutron exceeds the sum of the masses of the proton and electron. The process is called β-decay. It can also occur in a nucleus, but now the different binding energies of the initial neutron and the final proton must be factored in to decide if it will go. Other things being equal, the more neutrons there are present in the nucleus, the more likely it is to β-decay. Actually, β-decay was a big puzzle when it was first carefully observed, because it was discovered that identical nuclei β-decaying to the same final states ejected electrons over a range of energies, up to a maximum corresponding to the energy difference between the initial and final nuclei. This led to the suggestion that maybe, after all, energy wasn’t conserved in every process in nature.
But physicists are a conservative lot when it comes to energy conservation, and Pauli suggested that maybe n →p+e wasn’t the whole story—some other particle was being created at the same time, carrying away the balance of the energy, but undetected. This meant it had no charge, no mass, and, unlike the photon, no electric interaction. Fermi called it the neutrino, the little neutral one. Another reason the neutrino seemed necessary was that the initial neutron had spin one-half, as did the final proton and the emitted electron. It was difficult to see how angular momentum could be conserved if no other particle were emitted, because even if the final proton and electron had some orbital angular momentum, that comes in whole-number amounts, so how could two half-integer spins and an integer angular momentum add to be equal to the initial half-integer spin? It turned out they couldn’t, the neutrino really was there all along, it had spin one-half itself, but it was years before it was detected. Detecting neutrinos is still a difficult business, since they are not sensitive to the nuclear (strong) force, nor to electromagnetic fields. The force that causes neutron (and other particle) decay is called the weak force. The only way to detect a neutrino is if it collides with a particle and interacts weakly essentially reversing one of these decays. The problem is that a neutrino moving downwards is extremely unlikely to interact with a nucleus, it will almost certainly just pass through the earth. Therefore, to detect neutrinos takes large detectors and a strong flux of neutrinos. Much effort has been expended detecting neutrinos from the sun, since they are our only window into the nuclear processes taking place deep in the sun—they can get out unscathed, unlike photons or any other particle emitted. In fact, it is found that the number detected is less by a factor of two or three from that predicted using standard analyses of the solar nuclear processes. It turns out that in fact the neutrino is not quite massless, and there are actually three kinds of neutrinos! Furthermore, as a neutrino passes through matter, there is a nonzero probability of it changing from one kind to another. The solar nuclear processes generate what are called electron neutrinos, and the initial efforts at neutrino detection looked for that kind. More recent detectors count the other two kinds (mu neutrinos and tau neutrinos) as well, and the total number of neutrinos detected agrees well with the prediction of the total number generated in the sun, so it is now believed that some of the original electron neutrinos change types traveling from their point of origin to the sun’s surface.
Anyway, back to the radioactive decay of U238. It emits an α to become Th234, then β-decays twice in succession to become U234. This is now relatively proton-rich, and in fact α-decays five times in succession to become a form of lead,
U234 → Th230 → Ra226 → Rn222 → Po218 → Pb214.
Pb214 undergoes two β-decays, an α-decay and two more β-decays before it reaches stability at Pb206. The sequence above is through metallic elements with one exception—Rn, radon, is a gas because, atomically speaking, it has completely filled electron shells, and so is chemically unreactive, and gaseous at ordinary temperatures. It emits its α-particle in a period of days, which gives it time to diffuse out of the rock into somebody’s basement.
γ-decay
The three forms of radiation emitted by decaying nuclei, α, β and γ, were named before the particles being emitted were fully identified. It was only realized later that the β-rays were electrons. The γ-rays are just high-energy photons, of order 100 keV to a few MeV. Emission of γ-rays is similar (but at much higher energies) to emission of photons by excited states of atoms. The nucleus can be excited by having just emitted an α or β, or by colliding with another nucleus, or being bombarded by neutrons, say. All these events can lead to a nucleus in which the charge distribution is oscillating, and electromagnetic radiation ensues.
The Droplet Model
In some ways, the binding of nucleons in a nucleus is reminiscent of that of molecules in a drop of water—the force is attractive between near neighbors. Notice how different this is from the electrons in an atom, held in place by a large central attracting object. This “droplet” model of the nucleus is useful for understanding nuclear fission. If the droplet is somehow caused to vibrate vigorously, it might break into two, or more, smaller nuclei. For the U235 nucleus (only 0.7% in naturally occurring uranium), if a slow neutron gets too close, the attractive nuclear force pulls it towards the nucleus so strongly that in the resulting collision, the nucleus breaks into two smaller ones, and two or three neutrons are ejected (since the smaller nuclei formed have lower proportions of neutrons). There is also substantial energy release—about 200 MeV. The much more common U238 nucleus also attracts free neutrons, but not so strongly, and it survives neutron capture without fission.
A neutron has to be moving very slowly to be captured by U235. On the other hand, when U235 fissions the emitted neutrons are moving very fast. To get a chain reaction in a nuclear reactor, the main problem is to slow down the emitted neutrons before they leave the reactor. If they can be slowed down successfully, neutrons emitted by one fission will initiate further fissions, giving continuous—perhaps increasing—energy output. However, the neutrons bounce off the heavy uranium nuclei with almost no energy loss—to get a particle to lose energy in a collision, it must collide with something approximately its own size. Water is often used, the neutrons lose energy bouncing off the protons in the hydrogen atoms. Unfortunately, the neutrons often stick to the protons, forming deuterons, so to keep the reaction going the uranium must be enriched—the U235 content boosted to one to four percent. Of course, care must be taken to ensure that the chain reaction isn’t too successful—moderators, which absorb neutrons, are put into the reactor if the rate of fission increases beyond the planned level. Needless to say, moderators are not used in military applications of this concept.
Link to Chain Reaction Applet: scroll it down to read info.