Black Body Radiation

Michael Fowler, University of Virginia.

Query 8: Do not all fix’d Bodies, when heated beyond a certain degree, emit Light and shine; and is not this Emission perform’d by the vibrating motion of its parts?

Isaac Newton, Opticks, published 1704.

Heated Bodies Radiate

We shall now turn to another puzzle confronting physicists at the turn of the century (1900): just how do heated bodies radiate? There was a general understanding of the mechanism involved $—$ heat was known to cause the molecules and atoms of a solid to vibrate, and the molecules and atoms were themselves complicated patterns of electrical charges. (As usual, Newton was on the right track.) From the experiments of Hertz and others, Maxwell’s predictions that oscillating charges emitted electromagnetic radiation had been confirmed, at least for simple antennas. It was known from Maxwell’s equations that this radiation traveled at the speed of light and from this it was realized that light itself, and the closely related infrared heat radiation, were actually electromagnetic waves. The picture, then, was that when a body was heated, the consequent vibrations on a molecular and atomic scale inevitably induced charge oscillations. Assuming then that Maxwell’s theory of electromagnetic radiation, which worked so well in the macroscopic world, was also valid at the molecular level, these oscillating charges would radiate, presumably giving off the heat and light observed.

How is Radiation Absorbed?

What is meant by the phrase “black body” radiation? The point is that the radiation from a heated body depends to some extent on the body being heated. To see this most easily, let’s back up momentarily and consider how different materials absorb radiation. Some, like glass, seem to absorb light hardly at all—the light goes right through. For a shiny metallic surface, the light isn’t absorbed either, it gets reflected. For a black material like soot, light and heat are almost completely absorbed, and the material gets warm. How can we understand these different behaviors in terms of light as an electromagnetic wave interacting with charges in the material, causing these charges to oscillate and absorb energy from the radiation? In the case of glass, evidently this doesn’t happen, at least not much. Why not? A full understanding of why needs quantum mechanics, but the general idea is as follows: there are charges—electrons—in glass that are able to oscillate in response to an applied external oscillating electric field, but these charges are tightly bound to atoms, and can only oscillate at certain frequencies. (For quantum experts, these charge oscillations take place as an electron moves from one orbit to another. Of course, that was not understood in the 1890’s, the time of the first precision work on black body radiation.) It happens that for ordinary glass none of these frequencies corresponds to visible light, so there is no resonance with a light wave, and hence little energy absorbed. That’s why glass is perfect for windows! Duh. But glass is opaque at some frequencies outside the visible range (in general, both in the infrared and the ultraviolet). These are the frequencies at which the electrical charge distributions in the atoms or bonds can naturally oscillate.

How can we understand the reflection of light by a metal surface? A piece of metal has electrons free to move through the entire solid. This is what makes a metal a metal: it conducts both electricity and heat easily, both are actually carried by currents of these freely moving electrons. (Well, a little of the heat is carried by vibrations.) But metals are recognizable because they’re shiny $—$ why’s that? Again, it’s those free electrons: they’re driven into large (relative to the atoms) oscillations by the electrical field of the incoming light wave, and this induced oscillating current radiates electromagnetically, just like a current in a transmitting antenna. This radiation is the reflected light. For a shiny metal surface, little of the incoming radiant energy is absorbed as heat, it’s just reradiated, that is, reflected.

Now let’s consider a substance that absorbs light: no transmission and no reflection. We come very close to perfect absorption with soot. Like a metal, it will conduct an electric current, but nowhere near as efficiently. There are unattached electrons, which can move through the whole solid, but they constantly bump into things $—$ they have a short mean free path. When they bump, they cause vibration, like balls hitting bumpers in a pinball machine, so they give up kinetic energy into heat. Although the electrons in soot have a short mean free path compared to those in a good metal, they move very freely compared with electrons bound to atoms (as in glass), so they can accelerate and pick up energy from the electric field in the light wave. They are therefore very effective intermediaries in transferring energy from the light wave into heat.

Relating Absorption and Emission

Having seen how soot can absorb radiation and transfer the energy into heat, what about the reverse? Why does it radiate when heated? The pinball machine analogy is still good: imagine now a pinball machine where the barriers, etc., vibrate vigorously because they are being fed energy. The balls (the electrons) bouncing off them will be suddenly accelerated at each collision, and these accelerating charges emit electromagnetic waves. On the other hand, the electrons in a metal have very long mean free paths, the lattice vibrations affect them much less, so they are less effective in gathering and radiating away heat energy. It is evident from considerations like this that good absorbers of radiation are also good emitters.

In fact, we can be much more precise: a body emits radiation at a given temperature and frequency exactly as well as it absorbs the same radiation. This was proved by Kirchhoff: the essential point is that if we suppose a particular body can absorb better than it emits, then in a room full of objects all at the same temperature, it will absorb radiation from the other bodies better than it radiates energy back to them. This means it will get hotter, and the rest of the room will grow colder, contradicting the second law of thermodynamics. (We could use such a body to construct a heat engine extracting work as the room grows colder and colder!)

But a metal glows when it’s heated up enough: why is that? As the temperature is raised, the lattice of atoms vibrates more and more, these vibrations scatter and accelerate the electrons. Even glass glows at high enough temperatures, as the electrons are loosened and vibrate.

The “Black Body” Spectrum: a Hole in the Oven

Any body at any temperature above absolute zero will radiate to some extent, the intensity and frequency distribution of the radiation depending on the detailed structure of the body. To begin analyzing heat radiation, we need to be specific about the body doing the radiating: the simplest possible case is an idealized body which is a perfect absorber, and therefore also (from the above argument) a perfect emitter. For obvious reasons, this is called a “black body”.

But we need to check our ideas experimentally: so how do we construct a perfect absorber? OK, nothing’s perfect, but in 1859 Kirchhoff had a good idea: a small hole in the side of a large box is an excellent absorber, since any radiation that goes through the hole bounces around inside, a lot getting absorbed on each bounce, and has little chance of ever getting out again. So, we can do this in reverse: have an oven with a tiny hole in the side, and presumably the radiation coming out the hole is as good a representation of a perfect emitter as we’re going to find. Kirchhoff challenged theorists and experimentalists to figure out and measure (respectively) the energy/frequency curve for this “cavity radiation”, as he called it (in German, of course: hohlraumstrahlung, where hohlraum means hollow room or cavity, strahlung is radiation). In fact, it was Kirchhoff’s challenge in 1859 that led directly to quantum theory forty years later!

What Was Observed: Two Laws

The first quantitative conjecture based on experimental observation of hole radiation was:

Stefan’s Law (1879):

the total power $P$ radiated from one square meter of black surface at temperature $T$ goes as the fourth power of the absolute temperature:

$P = σ T^{4}, σ = 5.67 \times 10^{- 8} watts/sq .m {./K}^{4} .$

Five years later, in 1884, Boltzmann derived this $T^{4}$ behavior from theory: he applied classical thermodynamic reasoning to a box filled with electromagnetic radiation, using Maxwell’s equations to relate pressure to energy density. (The tiny amount of energy coming out of the hole would of course have the same temperature dependence as the radiation intensity inside.) See the accompanying notes for details of the derivation.

Exercise: the sun’s surface temperature is 5700K. How much power is radiated by one square meter of the sun’s surface? Given that the distance to earth is about 200 sun radii, what is the maximum power possible from a one square kilometer solar energy installation?

Wien’s Displacement Law (1893):

As the oven temperature varies, so does the frequency at which the emitted radiation is most intense. In fact, that frequency is directly proportional to the absolute temperature:

$f_{max} \propto T .$

(Wien himself deduced this law theoretically in 1893, following Boltzmann’s thermodynamic reasoning. It had previously been observed, at least semi-quantitatively, by an American astronomer, Langley.) The formula is derived in the accompanying notes.

In fact, this upward shift in $f_{max}$ with $T$ is familiar to everyone $—$ when an iron is heated in a fire, the first visible radiation (at around 900K) is deep red, the lowest frequency visible light. Further increase in $T$ causes the color to change to orange then yellow, and finally blue at very high temperatures (10,000K or more) for which the peak in radiation intensity has moved beyond the visible into the ultraviolet.

This shift in the frequency at which radiant power is a maximum is very important for harnessing solar energy, such as in a greenhouse. The glass must allow the solar radiation in, but not let the heat radiation out. This is feasible because the two radiations are in very different frequency ranges $—$ 5700K and, say, 300K $—$ and there are materials transparent to light but opaque to infrared radiation. Greenhouses only work because $f_{max}$ varies with temperature.

What Was Observed: the Complete Picture

By the 1890’s, experimental techniques had improved sufficiently that it was possible to make fairly precise measurements of the energy distribution in this cavity radiation, or as we shall call it black body radiation. In 1895, at the University of Berlin, Wien and Lummer punched a small hole in the side of an otherwise completely closed oven, and began to measure the radiation coming out.

The beam coming out of the hole was passed through a diffraction grating, which sent the different wavelengths/frequencies in different directions, all towards a screen. A detector was moved up and down along the screen to find how much radiant energy was being emitted in each frequency range. (This is a theorist’s model of the experiment—actual experimental arrangements were much more sophisticated. For example, to make the difficult infrared measurements higher frequency waves were eliminated by multiple reflections from quartz and other crystals.) They found a radiation intensity/frequency curve close to this (correct one):

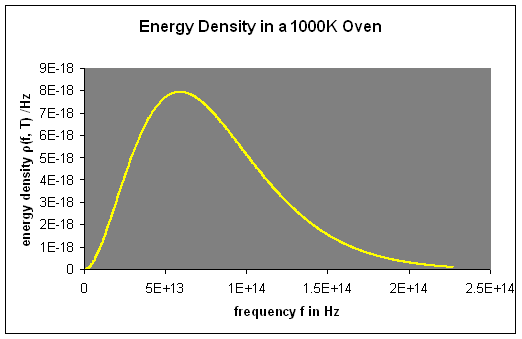
The visible spectrum begins at around 4.3×10¹⁴ Hz, so this oven glows deep red.

One minor point: this plot is the energy density inside the oven, which we denote by $ρ (f, T),$ meaning that at temperature $T,$ the energy in Joules/m³ in the frequency interval $f, f + Δ f$ is $ρ (f, T) Δ f .$

To find the power pumped out of the hole, bear in mind that the radiation inside the oven has waves equally going both ways $—$ so only half of them will come out through the hole. Also, if the hole has area A, waves coming from the inside at an angle will see a smaller target area. The result of these two effects is that the

radiation power from hole area $A = \frac{1}{4} A c ρ (f, T) .$

(Detailed derivation of the $\frac{1}{4}$ is in the notes.)

They were also able to confirm both Stefan’s Law $P = σ T^{4}$ and Wien’s Displacement Law by measuring the black body curves at different temperatures, for example:

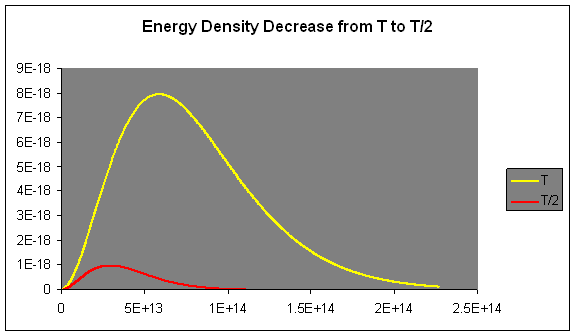
Let’s look at these curves in more detail: for low frequencies $f, ρ (f, T)$ was found to be proportional to $f^{2},$ a parabolic shape, but for increasing $f$ it fell below the parabola, peaking at $f_{max},$ then dropping quite rapidly towards zero as $f$ increased beyond $f_{max} .$

For those low frequencies where $ρ (f, T)$ is parabolic, doubling the temperature was found to double the intensity of the radiation. But also at $2 T$ the curve followed the doubled parabolic path much further before dropping away $—$ in fact, twice as far, and $f_{max} (2 T) = 2 f_{max} (T) .$

The curve $ρ (f, 2 T),$ then, reaches eight times the height of $ρ (f, T) .$ (See the graph above.) It also spreads over twice the lateral extent, so the area under the curve, corresponding to the total energy radiated, increases sixteenfold on doubling the temperature: Stefan’s Law, $P = σ T^{4} .$

Understanding the Black Body Curve

These beautifully precise experimental results were the key to a revolution. The first successful theoretical analysis of the data was by Max Planck in 1900. He concentrated on modeling the oscillating charges that must exist in the oven walls, radiating heat inwards and $—$ in thermodynamic equilibrium $—$ themselves being driven by the radiation field.

The bottom line is that he found he could account for the observed curve if he required these oscillators not to radiate energy continuously, as the classical theory would demand, but they could only lose or gain energy in chunks, called quanta, of size $h f,$ for an oscillator of frequency $f .$ The constant $h$ is now called Planck’s constant, $h = 6.626 \times 10^{- 34} joule \cdot \sec .$

With that assumption, Planck calculated the following formula for the radiation energy density inside the oven:

$ρ (f, T) d f = \frac{8 π V f^{2} d f}{c^{3}} \frac{h f}{e^{h f / k T} - 1} .$

The perfect agreement of this formula with precise experiments, and the consequent necessity of energy quantization, was the most important advance in physics in the century.

But no-one noticed for several years! His black body curve was completely accepted as the correct one: more and more accurate experiments confirmed it time and again, yet the radical nature of the quantum assumption didn’t sink in. Planck wasn’t too upset $—$ he didn’t believe it either, he saw it as a technical fix that (he hoped) would eventually prove unnecessary.

Part of the problem was that Planck’s route to the formula was long, difficult and implausible $—$ he even made contradictory assumptions at different stages, as Einstein pointed out later. But the result was correct anyway, and to understand why we’ll follow another, easier, route initiated (but not successfully completed) by Lord Rayleigh in England.

Rayleigh’s Sound Idea: Counting Standing Waves

In 1900, actually some months before Planck’s breakthrough work, Lord Rayleigh was taking a more direct approach to the radiation inside the oven: he didn’t even think about oscillators in the walls, he just took the radiation to be a collection of standing waves in a cubical enclosure: electromagnetic oscillators. In contrast to the somewhat murky reality of the wall oscillators, these standing electromagnetic waves were crystal clear.

This was a natural approach for Rayleigh—he’d solved an almost identical problem a quarter century earlier, an analysis of standing sound waves in a cubical room (§267 of his book). The task is to find and enumerate the different possible standing waves in the room/oven, compatible with the boundary conditions. For sound waves in a room, the amplitude of the sound goes to zero at the walls. For the electromagnetic waves, the electric field parallel to the wall must go to zero if the wall is a perfect conductor (and it’s OK to assume this—see note later).

So what are the allowed standing waves? As a warm up exercise, consider the different allowed modes of vibration, that is, standing waves, in a string of length $a$ fixed at both ends:

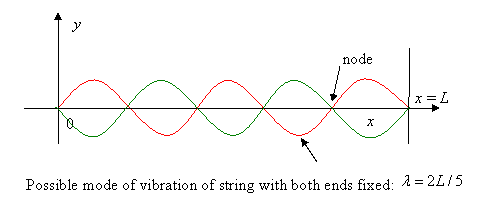
The possible values of wavelength are:

$λ = 2 a, a, 2 a / 3, \dots$

So the allowed frequencies are

$f = c / λ = c / 2 a, 2 (c / 2 a), 3 (c / 2 a), \dots$

These allowed frequencies are equally spaced $c / 2 a$ apart. We define the spectral density by stating that

number of modes between $f$ and $f + Δ f = N (f) Δ f$

where we assume that $Δ f$ is large compared with the spacing between successive frequencies. Evidently for this one-dimensional exercise $N (f)$ is a constant equal to $2 a / c,$ each mode corresponds to an integer point on the real axis in units $c / 2 a .$

The amplitude of oscillation as a function of time is:

$y = A \sin \frac{2 π x}{λ} \sin 2 π f t$

more conveniently written

$y = A \sin k x \sin ω t, where k = 2 π / λ, ω = 2 π f, so ω = c k .$

The allowed values of $k$ (called the wave number) are:

$k = 2 π / λ = π / a, 2 π / a, 3 π / a, \dots f = c k / 2 π .$

The generalization to three dimensions is simple: in a cubical box of side $a,$ an allowed standing wave must satisfy the boundary conditions in all three directions. This means the choices of wave numbers are:

$\begin{array}{l} k_{x} = 2 π / λ_{x} = π / a, 2 π / a, 3 π / a, \dots \\ k_{y} = 2 π / λ_{y} = π / a, 2 π / a, 3 π / a, \\ k_{z} = 2 π / λ_{z} = π / a, 2 π / a, 3 π / a, \dots \end{array}$

That is to say, each modes is labeled with three positive integers:

$(k_{x}, k_{y}, k_{z}) = \frac{π}{a} (l, m, n)$

and the frequency of the mode is:

$f = c k / 2 π = (c / 2 π) \sqrt{k_{x}^{2} + k_{y}^{2} + k_{z}^{2}} .$

(Details of the electromagnetic waves, and derivation of this formula, are given in the accompanying notes.)

For infrared and visible radiation in a reasonable sized oven, frequency intervals measured experimentally are far greater than the spacing $c / 2 a$ of these integer points. Just as in the one-dimensional example, these modes fill the three-dimensional $k$ -space uniformly, with density ${(a / π)}^{3},$ but now this means the mode density is not uniform as a function of frequency.

The number of them between $f$ and $f + Δ f = N (f) Δ f$ is the volume in $k$ -space, in units ${(π / a)}^{3},$ of the spherical shell of radius $k = 2 π f / c,$ thickness $Δ k = 2 π Δ f / c,$ and restricted to all components of $k$ being positive (like the integers), a factor of 1/8.

Including a factor of 2 for the two polarization states of the standing electromagnetic waves, the density of states as a function of frequency in an oven of volume $V = a^{3}$ is:

$N (f) Δ f = \frac{1}{8} \times 2 \times \frac{4 π k^{2} Δ k}{{(π / a)}^{3}} = \frac{1}{4} \times {(\frac{a}{π})}^{3} \times 4 π {(\frac{2 π}{c})}^{3} f^{2} Δ f$

giving the density of radiation states in the oven

$N (f) Δ f = \frac{8 V π f^{2} Δ f}{c^{3}} .$

(Details of this analysis can be found in the notes. If you’re wondering why it’s OK to have an oven with essentially perfectly reflecting walls when we were previously insisting on absorbing walls, Kirchhoff proved long before that two such ovens at the same temperature will have the same radiation intensity $—$ otherwise energy could be transferred from one to the other, violating the Second Law.)

What about Equipartition of Energy?

A central result of classical statistical mechanics is the equipartition of energy: for a system in thermal equilibrium, each degree of freedom has average energy $\frac{1}{2} k_{B} T .$ ( $k_{B}$ being Boltzmann's constant.) Thus molecules in a gas have average kinetic energy $\frac{3}{2} k_{B} T, \frac{1}{2} k_{B} T$ for each direction, and a simple one-dimensional harmonic oscillator has total energy $k_{B} T : \frac{1}{2} k_{B} T$ kinetic energy and $\frac{1}{2} k_{B} T$ potential energy.

Comparing now the formula for the number of modes $N (f) Δ f$ in a small interval $Δ f$

$N (f) Δ f = \frac{8 V π f^{2} Δ f}{c^{3}}$

with Planck’s formula for radiation energy intensity in the same interval:

$ρ (f, T) Δ f = \frac{8 π V f^{2} Δ f}{c^{3}} \frac{h f}{e^{h f / k_{B} T} - 1},$

for the low frequency modes $h f ≪ k_{B} T$ we can make the approximation

$e^{h f / k_{B} T} - 1 ≅ h f / k_{B} T$

and it follows immediately that each mode has energy $k_{B} T,$ in line with classical predictions.

But things go badly wrong at high frequencies! The number of modes increases without limit, the energy in these high frequency modes, though, is decaying exponentially as the frequency increases. Ehrenfest later dubbed this the ultraviolet catastrophe. Rayleigh’s sound approach apparently wasn’t so sound after all $—$ something crucial was missing.

It is perhaps surprising that Planck never mentioned equipartition. Of course, as Rayleigh himself remarked, equipartition was well-known to have problems, for example in the specific heat of gases. And in fact Planck wasn’t even sure about the existence of atoms: he later wrote that in the 1890’s “I had been inclined to reject atomism” (see notes). In fact, even Boltzmann was very unsure how well oscillators came to thermal equilibrium with electromagnetic radiation $—$ after all, it was well known that oscillation of diatomic molecules failed to reach classical thermal equilibrium with kinetic energy. (As long ago as 1877, Maxwell had pointed out that hot gases emit light at particular frequencies. The frequencies do not change with temperature, so the oscillations must be simple harmonic $—$ but such an oscillator would surely also be excited by collisions at low temperatures, so why was energy not being fed into this mode?)

Einstein Sees a Gas of Photons

As mentioned earlier, after Planck announced his result in December, 1900 there was a deafening silence on the subject for several years. No-one (including Planck) realized the importance of what he had done $—$ his work was widely seen as just a clever technical fix, even if it did give the right answer (the curve itself was completely accepted as correct).

Then in March, 1905, Albert Einstein turned his attention to the problem. He first rederived the Rayleigh result assuming equipartition:

$ρ (f, T) = \frac{8 π f^{2}}{c^{3}} k_{B} T$

and observed that this made no sense at high frequencies. So he focused on Planck’s formula for high frequencies, $h f ≫ k_{B} T :$

$ρ (f, T) d f ≅ \frac{8 π V h f^{3} d f}{c^{3}} e^{- h f / k_{B} T}$

(asymptotically identical for $f \to \infty$ to an earlier formula by Wien).

Einstein perceived an analogy here with the energy distribution in a classical gas.

Recall from the last lecture that the (normalized) probability distribution function for classical atoms as a function of speed $v$ was

$f (v) = 4 π {(\frac{m}{2 π k T})}^{3 / 2} v^{2} e^{- E / k_{B} T}$ ,

and the corresponding energy density in $E$ is

$f (E) = [4 π {(\frac{m}{2 π k T})}^{3 / 2} v^{2}] E e^{- E / k_{B} T} .$

The radiation formula at high frequencies is

$ρ (f, T) = \frac{8 π f^{2} h f}{c^{3}} e^{- h f / k_{B} T} .$

Einstein pointed out that if the high frequency radiation is imagined to be a gas of independent particles having energy $E = h f,$ the energy density in frequency/energy in the radiation is

$ρ (E, T) = [\frac{8 π f^{2}}{c^{3}}] E e^{- E / k_{B} T} .$

Comparing this with the expression for atoms, the analogy is close: recall that for the radiation, frequency is proportional to wave number and, on quantization, to momentum; for the (nonrelativistic) atoms velocity is proportional to momentum, so both these distributions are essentially in momentum space. Of course, the normalization factors differ, because the total number of atoms doesn’t change with temperature, unlike the total radiation. Nevertheless, the analogy is compelling, and led Einstein to state that the radiation in the enclosure was itself quantized, the energy quantization was not some special property only of the wall oscillators, as Planck thought. The radiation quanta are of course photons, but that word wasn’t coined until later.

Einstein had been troubled by Planck’s derivation of his result, depending as it did first, on a classical analysis of the interaction between the wall oscillator and radiation, followed by a claim that the interaction was in fact not like that at all. But the answer was right, and now Einstein began to see why. In contrast to the poorly understood wall oscillators, the electromagnetic standing wave oscillations in the oven were completely clear.

Energy in an Oscillator as a Function of Temperature

Einstein realized that, in terms of Rayleigh’s electromagnetic standing waves, the blackbody radiation curves have a simple interpretation: the average energy in an oscillator of frequency f at temperature T is

$\bar{E} = \frac{h f}{e^{h f / k_{B} T} - 1} .$

Furthermore, Planck’s work made plausible that this same quantization held for the material oscillators in the walls.

Einstein took the next step: he conjectured that all oscillators are quantized, for example a vibrating atom in a solid. This would explain why the Dulong Petit law, which assigns specific heat $3 k_{B}$ to each atom in a solid, does not hold good at low temperatures: once $k_{B} T ≪ h f,$ the modes are not excited, so absorb little heat. The specific heat falls, as is indeed observed. Furthermore, it explains why diatomic gas molecules, such as oxygen and nitrogen, do not appear to absorb heat into vibrational modes $—$ these modes have very high frequency.

It’s worth thinking about the constant exchange of energy with the environment for an oscillator in thermal equilibrium at temperature $T .$ The random thermal fluctuations in a system have energy of order $k_{B} T,$ this is the amount of energy, approximately, delivered back and forth. But if an oscillator has $h f = 5 k_{B} T,$ say, it can only accept chunks of energy of size $5 k_{B} T,$ and will only be excited in the unlikely event that five of these random $k_{B} T$ fluctuations come together at the right place at the right time. The high frequency modes are effectively frozen out by this minimum energy requirement. The exponential drop off in excitation with frequency reflects the exponential drop off in probability of getting the right number of fluctuations together, analogous to the exponential drop off in probability of tossing a coin n heads in a row.

Simple Derivation of Planck’s Formula from the Boltzmann’s Distribution

Planck’s essential assumption in deriving his formula was that the oscillators only exchange energy with the radiation in quanta $h f .$ Einstein made clear that the well-understood standing electromagnetic waves, the radiation in the oven, also have quantized energies.

As discussed in the previous lecture, the probability of a system at temperature $T$ having energy $E$ is proportional to $e^{- E / k_{B} T},$ Boltzmann’s formula. It turns out that this formula continues to be valid in quantum systems. Now, a classical simple harmonic oscillator at $T$ will have a probability distribution proportional to $e^{- E / k_{B} T} = e^{- (m v^{2} + m ω^{2} x^{2}) / 2 k_{B} T},$ so the expectation value of the energy is

$\bar{E} = \frac{\iint (\frac{1}{2} m v^{2} + \frac{1}{2} m ω^{2} x^{2}) e^{- (m v^{2} + m ω^{2} x^{2}) / 2 k_{B} T} d v d x}{\iint e^{- (m v^{2} + m ω^{2} x^{2}) / 2 k_{B} T} d v d x} = k_{B} T,$

just the classical equipartition of energy.

But we now know this isn’t true if the oscillator is quantized: the energies are now in steps $h f$ apart. Taking the ground state as the zero of energy, allowed energies are

$0, h f, 2 h f, 3 h f \dots$

and assuming the Boltzmann expression for relative probabilities is still correct, the relative probabilities of these states will be in the ratios:

$e^{- h f / k_{B} T}, e^{- 2 h f / k_{B} T}, e^{- 3 h f / k_{B} T} \dots$

To find the oscillator energy at this temperature, we use these probabilities weighted by the corresponding energy, and divide by a normalization factor to ensure that the probabilities add up to 1:

$\begin{matrix} \bar{E} = \frac{h f e^{- h f / k_{B} T} + 2 h f e^{- 2 h f / k_{B} T} + 3 h f e^{- 3 h f / k_{B} T} \dots}{1 + e^{- h f / k_{B} T} + e^{- 2 h f / k_{B} T} + e^{- 3 h f / k_{B} T} \dots} \\ = \frac{h f}{e^{h f / k_{B} T} - 1} . \end{matrix}$

(The expression is evaluated as follows: write $e^{- h f / k T} = x,$ so the sum of the relative probabilities is $1 + x + x^{2} + x^{3} + \dots = 1 / (1 - x),$ and the numerator in the above expression for $\bar{E}$ is $h f x (1 + 2 x + 3 x^{2} + \dots) = h f x / {(1 - x)}^{2},$ since the infinite series in parens is given by differentiating $1 + x + x^{2} + x^{3} + \dots$ )

This is indeed the correct result from the black body experiments. Evidently Boltzmann’s relative probability function $e^{- E / k_{B} T}$ is still valid in quantum systems.

A Note on Wien’s Displacement Law

It is easy to see how Wien’s Displacement Law follows from Planck’s formula: the maximum radiation per unit frequency range is at the frequency $f$ for which the function $f^{3} / (e^{h f / k_{B} T} - 1)$ is a maximum. Solving numerically gives $h f_{max} = 2.82 k_{B} T .$

It can be established theoretically (and is confirmed experimentally) that the equation connecting the frequency of maximum energy intensity in units of Joules/m³/Hz is:

$f_{max} = 5.88 \times 10^{10} T Hz/K .$

However, the law is often stated in terms of the wavelength at which the intensity, now measured in Joules/m³/m, that is, per unit interval of wavelength, and

$λ_{max} = \frac{2.9 \times 10^{- 3}}{T} m \cdot K .$

The important point to notice here is that these formulas do not give the same result, as is easily verified, since $f_{max} λ_{max} ≅ 1.7 \times 10^{8} m/sec$ , not the speed of light! The reason is that the two measures, per unit interval of frequency and per unit interval of wavelength, are different, so a claim that, say, sunlight is most intense in the yellow has to specify which is being used (actually it would be wavelength, frequency would give the near infrared).

The graphs of black body radiation as a function of temperature were generated using an Excel spreadsheet. You are welcome to download this spreadsheet and use it to explore how radiation varies with temperature. It’s very easy to use $—$ you just put in the temperature and watch the graph change.

DOWNLOAD SPREADSHEET

A nice example of black body radiation is that left over from the Big Bang. It has been found that the intensity pattern of this background radiation in the Universe follows the black body curve very precisely, for a temperature of about three degrees above absolute zero.

previous home next