Energy and Momentum in Lorentz Transformations

Michael Fowler, University of Virginia

How Does the Total Energy of a Particle Depend on Speed?

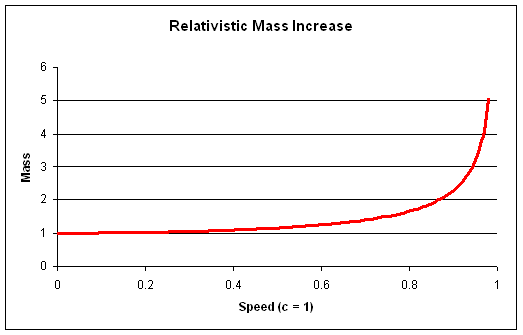
As in the earlier lecture, we follow Einstein and Feynman in using $m_{o}$ for the rest mass of a particle (or any object), $m$ for the “relativistic mass”, meaning that the total energy of the particle, the kinetic energy plus the energy tied up in the rest mass, is $E = m c^{2} .$ We established in the Relativistic Dynamics lecture that

$E = m c^{2} = \frac{m_{0} c^{2}}{\sqrt{1 - v^{2} / c^{2}}},$

From which we can plot how total energy $m c^{2}$ varies with speed:

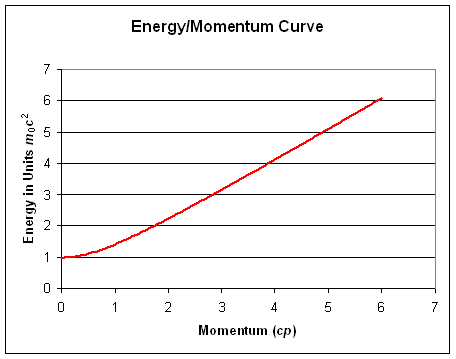
The momentum varies with speed as

$p = m v = \frac{m_{0} v}{\sqrt{1 - v^{2} / c^{2}}}$ .

How Does the Total Energy of a Particle Depend on Momentum?

It turns out to be useful to have a formula for $E$ in terms of $p .$

Now

$E^{2} = m^{2} c^{4} = \frac{m_{0}^{2} c^{4}}{1 - v^{2} / c^{2}}$

$\begin{array}{l} m^{2} c^{4} (1 - v^{2} / c^{2}) = m_{0}^{2} c^{4} \\ m^{2} c^{4} - m^{2} v^{2} c^{2} = m_{0}^{2} c^{4} \\ m^{2} c^{4} = E^{2} = m_{0}^{2} c^{4} + m^{2} c^{2} v^{2} \end{array}$

hence using $p = m v$ we find

$E = \sqrt{m_{0}^{2} c^{4} + c^{2} p^{2}}$ .

If $p$ is very small, this gives

$E \approx m_{0} c^{2} + \frac{p^{2}}{2 m_{0}}$ ,

the usual classical formula.

If $p$ is very large, so $c^{2} p^{2} ≫ m_{0}^{2} c^{4},$ the approximate formula is $E = c p .$

The High Kinetic Energy Limit: Rest Mass Becomes Unimportant!

Notice that this high energy limit is just the energy-momentum relationship Maxwell found to be true for light, for all $p .$ This could only be true for all $p$ if $m_{0}^{2} c^{4} = 0,$ that is, $m_{0} = 0.$

Light is in fact composed of “photons” $—$ particles having zero “rest mass”, as we shall discuss later. The “rest mass” of a photon is meaningless, since they’re never at rest $—$ the energy of a photon

$E = m c^{2} = \frac{m_{0} c^{2}}{\sqrt{1 - v^{2} / c^{2}}}$

is of the form 0/0, since $m_{0} = 0$ and $v = c,$ so “ $m$ ” can still be nonzero. That is to say, the mass of a photon is really all K.E. mass.

For very fast electrons, such as those produced in high energy accelerators, the additional K.E. mass can be thousands of times the rest mass. For these particles, we can neglect the rest mass and take $E = c p .$

Transforming Energy and Momentum to a New Frame

We have shown

$\begin{matrix} \vec{p} = m \vec{v} = \frac{m_{0} \vec{v}}{\sqrt{1 - v^{2} / c^{2}}} \\ E = m c^{2} = \sqrt{m_{0}^{2} c^{4} + c^{2} {\vec{p}}^{2}} . \end{matrix}$

Notice we can write this last equation in the form

$E^{2} - c^{2} {\vec{p}}^{2} = m_{0}^{2} c^{4} .$

That is to say, $E^{2} - c^{2} {\vec{p}}^{2}$ depends only on the rest mass of the particle and the speed of light. It does not depend on the velocity of the particle, so it must be the same $—$ for a particular particle $—$ in all inertial frames.

This is reminiscent of the invariance of ${\vec{x}}^{2} - c^{2} t^{2},$ the interval between two events, under the Lorentz transformations. One might guess from this that the laws governing the transformation from $E, p$ in one Lorentz frame to $E^{'}, p^{'}$ in another are similar to those for $t, x .$ We can actually derive the laws for $E, p$ to check this out.

As usual, we consider all velocities to be parallel to the $x$ -axis.

We take the frame S' to be moving in the $x$ -direction at speed $v$ relative to S.

Consider a particle of mass $m_{0}$ (rest mass) moving at $u^{'}$ in the $x^{'}$ direction in frame S', and hence at $u$ along $x$ in S, where

$u = \frac{u^{'} + v}{1 + v u^{'} / c^{2}} .$

The energy and momentum in S' are

$E^{'} = \frac{m_{0} c^{2}}{\sqrt{1 - {u^{'}}^{2} / c^{2}}}, p^{'} = \frac{m_{0} u^{'}}{\sqrt{1 - {u^{'}}^{2} / c^{2}}}$

and in S:

$E = \frac{m_{0} c^{2}}{\sqrt{1 - u^{2} / c^{2}}}, p = \frac{m_{0} u}{\sqrt{1 - u^{2} / c^{2}}} .$

Thus

$E = \frac{m_{0} c^{2}}{\sqrt{1 - {(\frac{u^{'} + v}{1 + v u^{'} / c^{2}})}^{2} / c^{2}}}$

giving

$E = \frac{m_{0} c^{2} (1 + v u^{'} / c^{2})}{\sqrt{(1 - v^{2} / c^{2}) (1 - {u^{'}}^{2} / c^{2})}}$

from which it is easy to show that

$E = \frac{1}{\sqrt{1 - v^{2} / c^{2}}} (E^{'} + v p^{'}) .$

Similarly, we can show that

$p = \frac{p^{'} + v E^{'} / c^{2}}{\sqrt{1 - v^{2} / c^{2}}} .$

These are the Lorentz transformations for energy and momentum of a particle $—$ it is easy to check that

$E^{2} - c^{2} p^{2} = {E^{'}}^{2} - c^{2} {p^{'}}^{2} = m_{0}^{2} c^{4} .$ .

Photon Energies in Different Frames

For a zero rest mass particle, such as a photon, $E = c p, E^{2} - c^{2} p^{2} = 0$ in all frames.

Thus

$E = \frac{E^{'} + v p^{'}}{\sqrt{1 - v^{2} / c^{2}}} = \frac{E^{'} + v E^{'} / c}{\sqrt{1 - v^{2} / c^{2}}} = E^{'} \sqrt{\frac{1 + v / c}{1 - v / c}} .$

Since $E = c p, E^{'} = c p^{'}$ we also have

$p = p^{'} \sqrt{\frac{1 + v / c}{1 - v / c}} .$

Notice that the ratios of photon energies in the two frames coincides with the ratio of photon frequencies found in the Doppler shift. As we shall see when we cover quantum mechanics, the photon energy is proportional to the frequency, so these two must of course transform in identical fashion. But it’s interesting to see it come about this way. Needless to say, relativity gives us no clue on what the constant of proportionality (Planck’s constant) is: it must be measured experimentally. But the same constant plays a role in all quantum phenomena, not just those concerned with photons.

previous home next