previous  home  next

The Lorentz Transformations

Michael Fowler, University of Virginia

Problems with the Galilean Transformations

We have already seen that Newtonian mechanics is invariant under the Galilean transformations relating two inertial frames moving with relative speed v in the x -direction,

x= x ′ +v t ′ , y= y ′ , z= z ′ , t= t ′ .

However, these transformations presuppose that time is a well-defined universal concept, that is to say, it’s the same time everywhere, and all observers can agree on what time it is.  Once we accept the basic postulate of special relativity, however, that the laws of physics, including Maxwell’s equations, are the same in all inertial frames of reference, and consequently the speed of light has the same value in all inertial frames, then as we have seen, observers in different frames do not agree on whether clocks some distance apart are synchronized.  Furthermore, as we have discussed, measurements of moving objects are compressed in the direction of motion by the Lorentz-Fitzgerald contraction effect.  Obviously, the above equations are too naïve!  We must think more carefully about time and distance measurement, and construct new transformation equations consistent with special relativity.

Our aim here, then, is to find a set of equations analogous to those above giving the coordinates of an event ( x,y,z,t ) in frame S, for example, a small bomb explosion, as functions of the coordinates ( x ′ , y ′ , z ′ , t ′ ) of the same event measured in the parallel frame S′ which is moving at speed v along the x -axis of frame S.  Observers O at the origin in frame S and O′ at the origin in frame S synchronize their clocks at t= t ′ =0, at the instant they pass each other, that is, when the two frames coincide . (Using our previous notation, O is Jack and O′ is Jill.)

To determine the time t ′ at which the bomb exploded in her frame, O′ could determine the distance of the point ( x ′ , y ′ , z ′ ) from her origin, and hence how long it would take light from the explosion to reach her at the origin. A more direct approach (which is helpful in considering transformations between different frames) is to imagine O′  to have a multitude of helpers, with an array of clocks throughout the frame, which have all been synchronized by midpoint flashes as described in the previous lecture.  Then the event—the bomb explosion—will be close to a clock, and that local clock determines the time t ′ of the event, so we do not need to worry about timing a light signal.

In frame S′, then, O′ and her crew have clocks all along the x ′ -axis (as well as everywhere else) and all synchronized:

Now consider how this string of clocks appears as viewed by O from frame S. First, since they are all moving at speed v, they will be registering time more slowly by the usual time dilation factor 1− v 2 / c 2 than O’s own physically identical clocks. Second, they will not be synchronized.  From the clocks on a train argument in the last lecture, if the clocks are L apart as measured by O′, successive clocks to the right (the direction of motion) will be behind by Lv/ c 2 as observed by O.

It should be mentioned that this lack of synchronization as viewed from another frame only occurs for clocks separated in the direction of relative motion. Consider two clocks some distance apart on the z ′ axis of S′.  If they are synchronized in S′  by both being started by a flash of light from a bulb half way between them, it is clear that as viewed from S the light has to go the same distance to each of the clocks, so they will still be synchronized (although they will start later by the time dilation factor).

Deriving the Lorentz Transformations

Let us now suppose that O′ and her crew observe a small bomb to explode in S′ at ( x ′ ,0,0, t ′ ).   In this section, we shall find the space coordinates and time ( x,y,z,t )  of this event as observed by O in the frame S.  (As above, S′ moves relative to S at speed v along the x -axis).  In other words, we shall derive the Lorentz transformations—which are just the equations giving the four coordinates of an event in one inertial frame in terms of the coordinates of the same event in another inertial frame.  We take y ′ , z ′ zero because they transform trivially—there is no Lorentz contraction perpendicular to the motion, so y= y ′  and z= z ′ .  

First, we consider at what time the bomb explodes as measured by O.  O′’s crew found the bomb to explode at time t ′ as measured by a local clock, that is, one located at the site of the explosion,  x ′ . Now, as observed by O from frame S, O′’s clock at x ′ is not synchronized with O′’s clock at her origin.  When the bomb explodes and the clock at x ′ reads t ′ , O will see O′’s origin clock to read t ′ +v x ′ / c 2 .  What does O′s own clock read at this point? Recall that O, O′ synchronized their origin clocks at the moment they were together, at t= t ′ =0.  Subsequently, O will have observed O′’s clock to be running slowly by the time-dilation factor. Therefore, when at the instant of the explosion he sees O′’s origin clock to be reading t ′ +v x ′ / c 2 , he will find that the true time t in his frame is equal to this appropriately scaled to allow for time dilation, that is,

t= t ′ +v x ′ / c 2 1− v 2 / c 2 .

This is the first of the Lorentz transformations.

The second question is: where does O observe the explosion to occur?

Since it occurs at time t after O′ passed O, O′ is vt meters beyond O at the time of the explosion.  The explosion takes place x ′ meters beyond O′, as measured by O′, but of course O will see that distance x ′ as contracted to x ′ 1− v 2 / c 2 since it’s in a moving frame.

Therefore O observes the explosion at point x given by

x=vt+ x ′ 1− v 2 / c 2 .

This can be written as an equation for x in terms of x ′ , t ′ by substituting for t using the first Lorentz transformation above, to give

x= x ′ +v t ′ 1− v 2 / c 2 .

Therefore, we have found the Lorentz transformations expressing the coordinates ( x,y,z,t ) of an event in frame S in terms of the coordinates ( x ′ , y ′ , z ′ , t ′ ) of the same event in frame S′:

x= x ′ +v t ′ 1− v 2 / c 2 , y= y ′ , z= z ′ , t= t ′ +v x ′ / c 2 1− v 2 / c 2 .

Notice that nothing in the above derivation depends on the x -velocity v of S′ relative to S being positive.  Therefore, the inverse transformation—from ( x,y,z,t ) to ( x ′ , y ′ , z ′ , t ′ ) --has exactly the same form as that given above with v replaced by −v. 

Spheres of Light

Consider now the following scenario: suppose that as O′ passes O (the instant both of them agree is at time t ′ =t=0 ) O′ flashes a bright light, which she observes to create an expanding spherical shell of light, centered on herself (imagine it’ s a slightly foggy day, so she can see how the ripple of light travels outwards). At time t ′ , then, O′ (or, to be precise, her local observers out there in the frame) will see a shell of light of radius c t ′ , that is to say, they will see the light to have reached all points ( x ′ , y ′ , z ′ ) on the surface

x ′ 2 + y ′ 2 + z ′ 2 = c 2 t ′ 2 .

Question: how do O and his observers stationed throughout the frame S see this light as rippling outwards?

To answer this question, notice that the above equation for where the light is in frame S′ at a particular time t ′ can be written

x ′ 2 + y ′ 2 + z ′ 2 − c 2 t ′ 2 =0,

and can be thought of as a surface in the four dimensional ( x ′ , y ′ , z ′ , t ′ ) space, the totality of all the “events” of the light reaching any particular point. Now, to find the corresponding surface of events in the four dimensional ( x,y,z,t ) space, all we have to do is to change from one set of variables to the other using the Lorentz transformations:

x ′ = x−vt 1− v 2 / c 2 y ′ =y z ′ =z t ′ = t−vx/ c 2 1− v 2 / c 2 .

On putting these values of ( x ′ , y ′ , z ′ , t ′ ) into x ′ 2 + y ′ 2 + z ′ 2 − c 2 t ′ 2 =0, we find that the corresponding surface of events in ( x,y,z,t ) space is:

x 2 + y 2 + z 2 − c 2 t 2 =0.

This means that at time t, O and his observers in frame S will say the light has reached a spherical surface centered on O.

How can O′ and O, as they move further apart, possibly both be right in maintaining that at any given instant the outward moving light pulse has a spherical shape, each saying it is centered on herself or himself?

Imagine the light shell as O′ sees it—at the instant t ′ she sees a sphere of radius r ′ , in particular she sees the light to have reached the spots + r ′ and − r ′ on the x ′ -axis.  But from O′’s point of view the expanding light sphere does not reach the point + r ′ at the same time it reaches − r ′!  (This is just the old story of synchronizing the two clocks at the front and back of the train one more time.)  That is why O does not see O′’s sphere:  the arrival of the light at the sphere of radius r ′ around O′ at time t ′ corresponds in S to a continuum of different events happening at different times.

Lorentz Invariants

We found above that for an event ( x ′ , y ′ , z ′ , t ′ ) for which x ′ 2 + y ′ 2 + z ′ 2 − c 2 t ′ 2 =0, the coordinates of the event ( x,y,z,t ) as measured in the other frame S satisfy x 2 + y 2 + z 2 − c 2 t 2 =0.  The quantity x 2 + y 2 + z 2 − c 2 t 2 is said to be a Lorentz invariant:  it doesn’t vary on going from one frame to another.

A simple two-dimensional analogy to this invariant is given by considering two sets of axes, Oxy and Ox′ y′  having the same origin O, but the axis Ox′  is at an angle to Ox, so one set of axes is the same as the other set but rotated.  The point P with coordinates ( x,y ) has coordinates ( x ′ , y ′ ) measured on the Ox′ y′  axes.  The square of the distance of the point P from the common origin O is x 2 + y 2 and is also x ′ 2 + y ′ 2 , so for the transformation from coordinates ( x,y ) to ( x ′ , y ′ ),  x 2 + y 2  is an invariant.  Similarly, if a point P₁ has coordinates ( x 1 , y 1 ) and ( x ′ 1 , y ′ 1 ) and another point P₂ has coordinates ( x 2 , y 2 ) and ( x ′ 2 , y ′ 2 ) then clearly the two points are the same distance apart as measured with respect to the two sets of axes, so

( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 = ( x ′ 1 − x ′ 2 ) 2 + ( y ′ 1 − y ′ 2 ) 2 . 

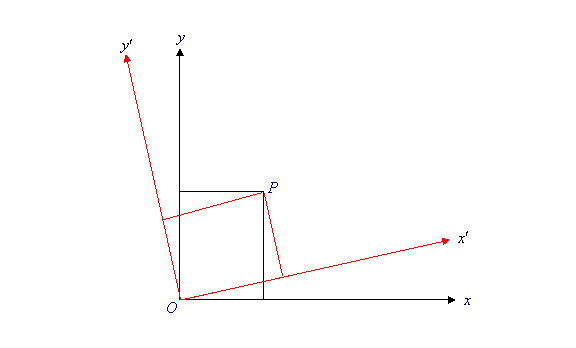
This is really obvious:  the distance between two points in an ordinary plane can’t depend on the angle at which we choose to set our coordinate axes.

The Lorentz analog of this, dropping the y,z coordinates, can be written

c 2 ( t 1 − t 2 ) 2 − ( x 1 − x 2 ) 2 = c 2 ( t ′ 1 − t ′ 2 ) 2 − ( x ′ 1 − x ′ 2 ) 2 = s 2 ,

say, where s 2 is some sort of measure of the “distance” between the two events ( x 1 , t 1 ) and ( x 2 , t 2 ). 

This s 2 is sometimes called the “space-time interval”.  The big difference from the two-dimensional rotation case is that, despite the notation,  s² can be positive or negative.   The cases of spacelike and timelike separated events are best dealt with separately, at least to begin with.

Consider first two events simultaneous in frame S′, so t ′ 1 = t ′ 2 .  They will not be simultaneous in frame S, but they will satisfy

( x 1 − x 2 ) 2 − c 2 ( t 1 − t 2 ) 2 >0.

We say the two events are spacelike separated.  This means that they are sufficiently removed spatially that a light signal could not have time between them to get from one to the other, so one of these events could not be the cause of the other.  The sequence of two events can be different in different frames if the events are spacelike separated.  Consider again the starting of the two clocks at the front and back of a train as seen from the ground: the back clock starts first.  Now imagine viewing this from a faster train overtaking the clock train—from this view, the front clock will be the first to start.  The important point is that although these events appear to occur in a different order in a different frame, neither of them could be the cause of the other, so cause and effect are not switched around.

Consider now two events which occur at the same place in frame S′ at different times,  ( x ′ 1 , t ′ 1 ) and ( x ′ 2 , t ′ 1 ).  Then in frame S:

c 2 ( t 1 − t 2 ) 2 − ( x 1 − x 2 ) 2 = c 2 ( t ′ 1 − t ′ 2 ) 2 >0.

These events are said to be timelike separated.  There is no frame in which they are simultaneous.  “Cause and effect” events are timelike separated.

The Light Cone

Let us try to visualize the surface in four-dimensional space described by the outgoing shell of light from a single flash,

x 2 + y 2 + z 2 − c 2 t 2 =0.

It is helpful to think about a simpler situation, the circular ripple spreading on the surface of calm water from a pebble falling in. Taking c here to be the speed of the water waves, it is easy to see that at time t after the splash the ripple is at

x 2 + y 2 − c 2 t 2 =0.

Now think about this as a surface in the three-dimensional space ( x,y,t ).  The plane corresponding to time t cuts this surface in a circle of radius ct. This means the surface is a cone with its point at the origin.  (The four-dimensional space flash-of-light surface is not so easy to visualize, but is clearly the higher-dimensional analog: the plane surface corresponding to time t cuts it in a sphere instead of a circle.)  This surface is called the lightcone.

We have stated above that the separation of a point P ( x,y,z,t ) from the origin is spacelike if x 2 + y 2 + z 2 − c 2 t 2 >0,  and timelike if x 2 + y 2 + z 2 − c 2 t 2 <0.  

 It is said to be lightlike if x 2 + y 2 + z 2 − c 2 t 2 =0.  

Points on the light cone described above are lightlike separated from the origin.  To be precise, the points corresponding to an outgoing shell of light from a flash at the origin at t=0 form the forward light cone. Since the equation depends only on t 2 , there is a solution with t negative, the “backward light cone”, just the reflection of the forward light cone in the plane t=0. 

Possible causal connections are as follows: an event at the origin (0, 0, 0, 0) could cause an event inside or on the forward light cone: so that is the “future”, as seen from the origin.  Events in the backward light cone—the “past”—could cause an event at the origin. There can be no causal link between an event at the origin and an event outside the light cones, since the separation is spacelike: outside the light cones is “elsewhere” as viewed from the origin.

previous  home  next