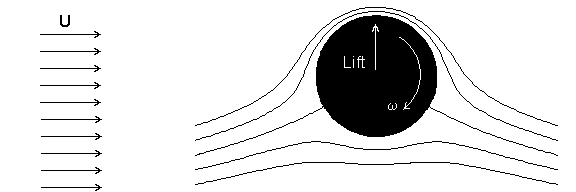
We've already encountered the Magnus force in our discussion of the flow of a nonviscous fluid around a cylinder. Recall that the drag force is always zero, but that there could be a lifting force if there is circulation of the fluid around the cylinder. There is no paradox here--the lifting force is directed perpendicular to the cylinder velocity (or the free stream velocity if the cylinder is stationary), so that the Magnus force does no work on the cylinder. The combined flow has a higher velocity, and hence a lower pressure, on the top surface, leading to a pressure imbalance and a net upward force on the cylinder--see the figure.
Figure 4.1: The Magnus force, or lift, on a spinning cylinder in a non-viscous fluid.
The magnitude of the lifting force per unit length of the cylinder is 
, where 
is the density of the fluid, U is the free
stream velocity, and 
is the circulation. What determines ?
In a viscous fluid we could induce such a flow by spinning the cylinder; the
no-slip boundary condition would cause the fluid surrounding the cylinder to
spin with it. In this case 
, where
v is the velocity of a point on the surface of the ball. Since 
,
with 
the angular velocity, then
.
A golf ball or a tennis ball which has backspin (due to it being "undercut") will experience a Magnus force, causing it to rise. The longer "hang time" of the spinning golf ball leads to longer drives. In fact, experienced golfers play with somewhat softer balls, which adhere more readily to the face of the club and receive a larger angular momentum (and angular velocity). A less experienced golfer will tend to slice such a ball, maiming innocent bystanders (a feat accomplished by many presidential golfers). Conversely, a tennis ball with a heavy topspin will "drop" into the opponent's court.
