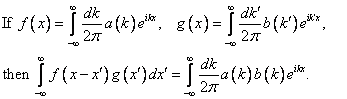Physics 751 Homework #2
Due Friday September 12, 2008 11:00 am.
1. (a) Defining the delta function as the limit of a narrow Gaussian wave packet (see the web notes on Fourier Series, etc.) prove it has the following properties:
![]()
![]()
![]()
(b) Suppose you define the delta function by:
![]()
Does this function have all the above properties?
2.
Use Mathematica, Maple or Integral Tables to find the integral of
(sinx)/x from 0 to ![]() and from 0 to
infinity. Use your result to estimate the overshoot that appears in a Fourier
series representation of a step function (Gibbs’ phenomenon).
and from 0 to
infinity. Use your result to estimate the overshoot that appears in a Fourier
series representation of a step function (Gibbs’ phenomenon).
3.
Suppose at t = 0, a free particle of mass m, in one dimension,
has a Gaussian wavefunction
![]()
By taking a Fourier transform and putting in the explicit time-dependence for each plane wave component, find the form of the wavefunction as a function of time, and provide a physical interpretation in terms of finding the particle somewhere.
4.
Denoting the lowest energy eigenstate in an infinite square well by ![]() , and the first excited state by
, and the first excited state by ![]() , describe the behavior of the probability distribution as a
function of time for the state
, describe the behavior of the probability distribution as a
function of time for the state ![]() (appropriately
normalized).
(appropriately
normalized).
Find the probability current at the midpoint of the well as a function of time.
How
would your analysis be different for the state ![]() ?
?
5. Prove Parseval’s Theorem:
![]()
6. Prove the rule for the Fourier Transform of a convolution of two functions: