Physics 751 Homework # 3
Due Friday September 19,
2008
1. For ![]() , find the Fourier series for the delta function
, find the Fourier series for the delta function ![]() .
.
2. Find the Fourier series for the triangular wave
![]()
What is the derivative of this function? What is its second derivative? Do the Fourier series correctly represent these functions?
3. Suppose we define the inner product for real functions defined on the infinite line to be:
![]()
Starting with the polynomials 1, x, x2, x3, … , construct the first four members of an orthonormal basis.
4. (a) Define the derivative of the delta function by

Sketch this function for small D.
What is the value of ![]() ?
?
(b) Sketch a similar function whose limit is the second derivative of the delta function.
5. (a) If U and V are unitary, is UV unitary? Prove your result.
(b) If A and B are Hermitian, is AB Hermitian? Prove your result.
6. If H is Hermitian, prove
(a) U = eiH is unitary,
(b) log det U = iTrH.
7. Prove that a Hermitian matrix satisfies its own characteristic equation (that is, the polynomial equation whose roots are the eigenvalues).
8. Find the eigenvalues and eigenvectors of the 2×2 matrix
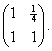
Prove that the eigenvectors are not orthogonal. Why does the argument we gave in lectures that the eigenvectors of a Hermitian matrix are orthogonal fail here?
9. Find the eigenvalues and eigenvectors of the following matrices:
![]()
State which of these matrices are Hermitian, and which are unitary.