
Newton's Life
In 1642, the year Galileo died, Isaac Newton was born in Woolsthorpe, Lincolnshire, England on Christmas Day. His father had died three months earlier, and baby Isaac, very premature, was also not expected to survive. It was said he could be fitted into a quart pot. When Isaac was three, his mother married a wealthy elderly clergyman from the next village, and went to live there, leaving Isaac behind with his grandmother. The clergyman died, and Isaac's mother came back, after eight years, bringing with her three small children. Two years later, Newton went away to the Grammar School in Grantham, where he lodged with the local apothecary, and was fascinated by the chemicals. The plan was that at age seventeen he would come home and look after the farm. He turned out to be a total failure as a farmer.
His mother's brother, a clergyman who had been an undergraduate at Cambridge, persuaded his mother that it would be better for Isaac to go to university, so in 1661 he went up to Trinity College, Cambridge. Isaac paid his way through college for the first three years by waiting tables and cleaning rooms for the fellows (faculty) and the wealthier students. In 1664, he was elected a scholar, guaranteeing four years of financial support. Unfortunately, at that time the plague was spreading across Europe, and reached Cambridge in the summer of 1665. The university closed, and Newton returned home, where he spent two years concentrating on problems in mathematics and physics. He wrote later that during this time he first understood the theory of gravitation, which we shall discuss below, and the theory of optics (he was the first to realize that white light is made up of the colors of the rainbow), and much mathematics, both integral and differential calculus and infinite series. However, he was always reluctant to publish anything, at least until it appeared someone else might get credit for what he had found earlier.
On returning to Cambridge in 1667, he began to work on alchemy, but then in 1668 Nicolas Mercator published a book containing some methods for dealing with infinite series. Newton immediately wrote a treatise, De Analysi, expounding his own wider ranging results. His friend and mentor Isaac Barrow communicated these discoveries to a London mathematician, but only after some weeks would Newton allow his name to be given. This brought his work to the attention of the mathematics community for the first time. Shortly afterwards, Barrow resigned his Lucasian Professorship (which had been established only in 1663, with Barrow the first incumbent) at Cambridge so that Newton could have the Chair.
Newton's first major public scientific achievement was the invention, design and construction of a reflecting telescope. He ground the mirror, built the tube, and even made his own tools for the job. This was a real advance in telescope technology, and ensured his election to membership in the Royal Society. The mirror gave a sharper image than was possible with a large lens because a lens focusses different colors at slightly different distances, an effect called chromatic aberration. This problem is minimized nowadays by using compound lenses, two lenses of different kinds of glass stuck together, that err in opposite directions, and thus tend to cancel each other's shortcomings, but mirrors are still used in large telescopes.
Later in the 1670's, Newton became very interested in theology. He studied Hebrew scholarship and ancient and modern theologians at great length, and became convinced that Christianity had departed from the original teachings of Christ. He felt unable to accept the current beliefs of the Church of England, which was unfortunate because he was required as a Fellow of Trinity College to take holy orders. Happily, the Church of England was more flexible than Galileo had found the Catholic Church in these matters, and King Charles II issued a royal decree excusing Newton from the necessity of taking holy orders! Actually, to prevent this being a wide precedent, the decree specified that, in perpetuity, the Lucasian professor need not take holy orders. (The current Lucasian professor is Stephen Hawking.)
In 1684, three members of the Royal Society, Sir Christopher Wren, Robert Hooke and Edmond Halley, argued as to whether the elliptical orbits of the planets could result from a gravitational force towards the sun proportional to the inverse square of the distance. Halley writes:
Mr. Hook said he had had it, but that he would conceal it for some time so that others, triing and failing might know how to value it, when he should make it publick.
Halley went up to Cambridge, and put the problem to Newton, who said he had solved it four years earlier, but couldn't find the proof among his papers. Three months later, he sent an improved version of the proof to Halley, and devoted himself full time to developing these ideas, culminating in the publication of the Principia in 1686. This was the book that really did change man's view of the universe, as we shall shortly discuss, and its importance was fully appreciated very quickly. Newton became a public figure. He left Cambridge for London, where he was appointed Master of the Mint, a role he pursued energetically, as always, including prosecuting counterfeiters. He was knighted by Queen Anne. He argued with Hooke about who deserved credit for discovering the connection between elliptical orbits and the inverse square law until Hooke died in 1703, and he argued with a German mathematician and philosopher, Leibniz, about which of them invented calculus. Newton died in 1727, and was buried with much pomp and circumstance in Westminster Abbey, despite his well-known reservations about the Anglican faith.
An excellent, readable book is The Life of Isaac Newton, by Richard Westfall, Cambridge 1993, which I used in writing the above summary of Newton's life.
A fascinating collection of articles, profusely illustrated, on Newton's life, work and impact on the general culture is Let Newton Be!, edited by John Fauvel and others, Oxford 1988, which I also consulted.
Projectiles and Planets
Let us now turn to the central topic of the Principia, the universality of the gravitational force. The legend is that Newton saw an apple fall in his garden in Lincolnshire, thought of it in terms of an attractive gravitational force towards the earth, and realized the same force might extend as far as the moon. He was familiar with Galileo's work on projectiles, and suggested that the moon's motion in orbit could be understood as a natural extension of that theory. To see what is meant by this, consider a gun shooting a projectile horizontally from a very high mountain, and imagine using more and more powder in successive shots to drive the projectile faster and faster.
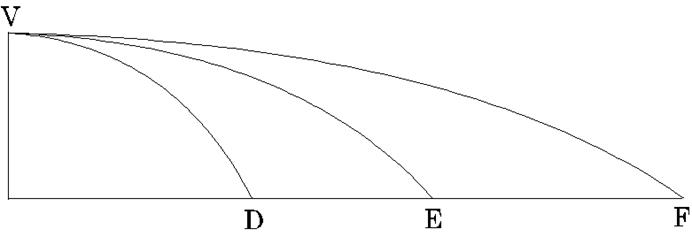
The parabolic paths would become flatter and flatter, and, if we imagine that the mountain is so high that air resistance can be ignored, and the gun is sufficiently powerful, eventually the point of landing is so far away that we must consider the curvature of the earth in finding where it lands.
In fact, the real situation is more dramatic: the earth's curvature may mean the projectile never lands at all. This was envisioned by Newton in the Principia. The following diagram is from his later popularization, A Treatise of the System of the World, written in the 1680's:
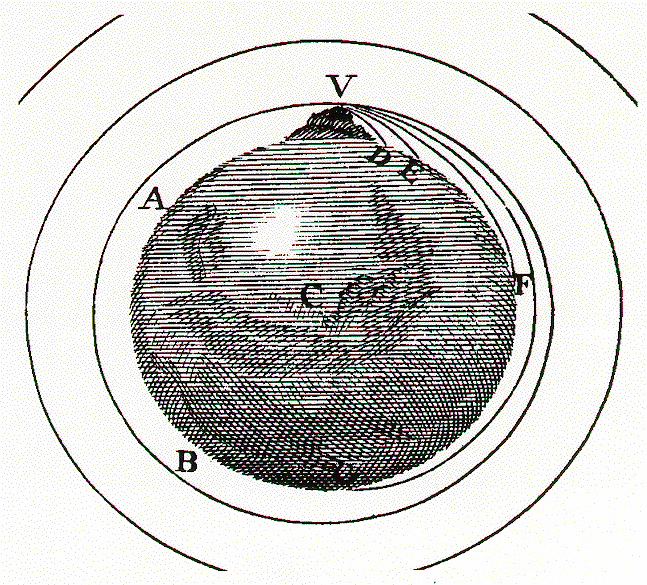
The mountaintop at V is supposed to be above the earth's atmosphere, and for a suitable initial speed, the projectile orbits the earth in a circular path. In fact, the earth's curvature is such that the surface falls away below a truly flat horizontal line by about five meters in 8,000 meters (five miles). Recall that five meters is just the vertical distance an initially horizontally moving projectile will fall in the first second of motion. But this implies that if the (horizontal) muzzle velocity were 8,000 meters per second, the downward fall of the cannonball would be just matched by the earth's surface falling away, and it would never hit the ground! This is just the motion, familiar to us now, of a satellite in a low orbit, which travels at about 8,000 meters (five miles) a second, or 18,000 miles per hour. (Actually, Newton drew this mountain impossibly high, no doubt for clarity of illustration. A satellite launched horizontally from the top would be far above the usual shuttle orbit, and go considerably more slowly than 18,000 miles per hour.)
For an animated version of Newton's cannon on a mountain, click here!
The Moon is Falling
Newton realized that the moon's circular path around the earth could be caused in this way by the same gravitational force that would hold such a cannonball in low orbit, in other words, the same force that causes bodies to fall.
To think about this idea, let us consider the moon's motion, beginning at some particular instant, as deviating downwards -- falling -- from some initial horizontal line, just as for the cannonball shot horizontally from a high mountain. The first obvious question is: does the moon fall five meters below the horizontal line, that is, towards the earth, in the first second? This was not difficult for Newton to check, because the path of the moon was precisely known by this time. The moon's orbit is approximately a circle of radius about 384,000 kilometers (240,000 miles), which it goes around in a month (to be precise, in 27.3 days), so the distance covered in one second is, conveniently, very close to one kilometer. It is then a matter of geometry to figure out how far the curved path falls below a "horizontal" line in one second of flight, and the answer turns out to be not five meters, but only a little over one millimeter! (Actually around 1.37 millimeters.)
It's completely impossible to draw a diagram showing how far it falls in one
second, but the geometry is the same if we look how far it falls in one day,
so here it is:

For one second, AB would be only one kilometer, so since AC is 384,000 km, the triangle ABC is really thin, but we can still use
Pythagoras' theorem!
Thus the "natural acceleration" of the moon towards the earth, measured by how far it falls below straight line motion in one second, is less than that of an apple here on earth by the ratio of five meters to 1.37 millimeters, which works out to be about 3,600.
What can be the significance of this much smaller rate of fall? Newton's answer was that the natural acceleration of the moon was much smaller than that of the cannonball because they were both caused by a force: a gravitational attraction towards the earth, and that the gravitational force became weaker on going away from the earth.
In fact, the figures we have given about the moon's orbit enable us to compute how fast the gravitational attraction dies away with distance. The distance from the center of the earth to the earth's surface is about 6,350 kilometers (4,000 miles), so the moon is about 60 times further from the center of the earth than we and the cannonball are.
From our discussion of how fast the moon falls below a straight line in one second in its orbit, we found that the gravitational acceleration for the moon is down by a factor of 3,600 from the cannonball's (or the apple's).
Putting these two facts together, and noting that 3,600 = 60 x 60, led Newton to his famous inverse square law: the force of gravitational attraction between two bodies decreases with increasing distance between them as the inverse of the square of that distance, so if the distance is doubled, the force is down by a factor of four.