previous
index
next
PDF
How Newton Built on Galileo's Ideas
How Newton built on Galileo's Ideas
Michael Fowler, UVa
Newton's Laws
We are now ready to move on to Newton's Laws of Motion,
which for the first time presented a completely coherent analysis of motion,
making clear that the motion in the heavens could be understood in the same
terms as motion of ordinary objects here on Earth.
Acceleration Again
The crucial Second Law, as we shall see below, links the acceleration
of a body with the force acting on the body. To understand what it says, it is
necessary to be completely clear what is meant by acceleration, so let us
briefly review.
Speed is just how fast something's moving, so is fully specified by a
positive number and suitable units, such as 55 mph or 10 meters per second.
Velocity, on the other hand, means to a scientist more than
speed---it also includes a specification of the direction of the
motion, so 55 mph to the northwest is a velocity. Usually wind velocities
are given in a weather forecast, since the direction of the wind affects future
temperature changes in a direct way. The standard way of representing a
velocity in physics is with an arrow pointing in the appropriate direction, its
length representing the speed in suitable units. These arrows are called "vectors".
(WARNING: Notice, though, that for a moving object such as a projectile, both
its position at a given time (compared with where it started) and its
velocity at that time can be represented by vectors, so you must be clear what
your arrow represents!)
Acceleration: as we have stated, acceleration is defined as rate
of change of velocity.
It is not defined as rate of change of speed. A body can have nonzero acceleration while moving at constant speed!
An Accelerating Body that isn't Changing Speed
Consider Newton's cannon on an imaginary high mountain above the atmosphere,
that shoots a ball so fast it circles the Earth at a steady speed. Of
course, its velocity is changing constantly, because velocity includes
direction.
Here's the animation.
Let us look at how its velocity changes over a period of one second.
(Actually, in the diagram below we exaggerate how far it would move in one
second, the distance would in fact be one-five thousandth of the distance around
the circle, impossible to draw.)
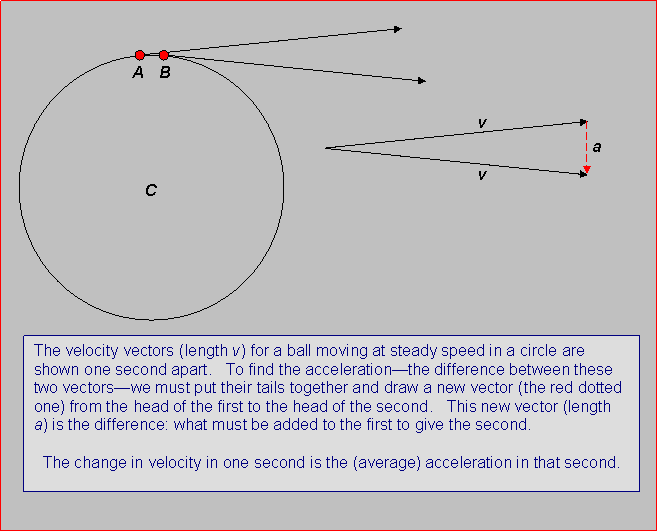
Here we show the cannonball (greatly exaggerated in size!) at two points in
its orbit, and the velocity vectors at those points. On the right, we show the
two velocity vectors again, but we put their ends together so that we can see
the difference between them, which is the small dashed vector.
In other words, the small dashed vector is the velocity that has to be added
to the first velocity to get the second velocity: it is the change in velocity
on going around that bit of the orbit.
Now, if we think of the two points in the orbit as corresponding to
positions of the cannonball one second apart, the small dashed vector will
represent the change in velocity in one second, and that is -- by definition -- the
acceleration. The acceleration is the rate of change of velocity, and that is
how much the velocity changes in one second (for motions that change reasonably
smoothly over the one-second period, which is certainly the case here. To find
the rate of change of velocity of a fly's wing at some instant, we obviously
would have to measure its velocity change over some shorter interval, maybe a
thousandth of a second).
So we see that, with our definition of acceleration as the rate of change of
velocity, which is a vector, a body moving at a steady speed around a circle is
accelerating towards the center all the time, although it never gets any closer
to it. If this thought makes you uncomfortable, it is because you are still thinking that acceleration must mean a change of speed, and just changing direction doesn’t count.
Finding the Acceleration in Circular Motion
It is possible to find an explicit expression for the magnitude of the
acceleration towards the center (sometimes called the centripetal acceleration)
for a body moving on a circular path at speed v. Look again at the
diagram above showing two values of the velocity of the cannonball one second
apart. As is explained above, the magnitude a of the acceleration is
the length of the small dashed vector on the right, where the other two sides
of this long narrow triangle have lengths equal to the speed v of the
cannonball. We'll call this the vav triangle, because those are the
lengths of its sides. What about the angle between the two long sides? That
is just the angle the velocity vector turns through in one second as the
cannonball moves around its orbit. Now look over at the circle diagram on the
left showing the cannonball's path. Label the cannonball's position at the
beginning of the second A, and at the end of the second B, so the
length AB is how far the cannonball travels in one second, that is, v.
(It's true that the part of the path AB is slightly curved, but we can
safely ignore that very tiny effect.) Call the center of the circle C.
Draw the triangle ACB. (The reader should
sketch the figure and actually draw these triangles!) The two long
sides AC and BC have lengths equal to the radius of the circular
orbit. We could call this long thin triangle an rvr triangle, since
those are the lengths of its sides.
The important point to realize now is that the vav triangle and the
rvr triangle are similar, because since the velocity vector is
always perpendicular to the radius line from the center of the circle to the
point where the cannonball is in orbit, the angle the velocity vector
rotates by in one second is the same as the angle the radius line turns through
in one second. Therefore, the two triangles are similar, and their
corresponding sides are in the same ratios, that is, a/v = v/r.
It follows immediately that the magnitude of the
acceleration a for an object moving at steady speed v in a circle of radius r
is v2/r directed towards the center of the circle.
This result is true for all circular motions, even those where the moving
body goes round a large part of the circle in one second. To establish it in a
case like that, recall that the acceleration is the rate of change of velocity,
and we would have to pick a smaller time interval than one second, so that the
body didn't move far around the circle in the time chosen. If, for example, we
looked at two velocity vectors one-hundredth of a second apart, and they were
pretty close, then the acceleration would be given by the difference vector
between them multiplied by one-hundred, since acceleration is defined as
what the velocity change in one second would be if it continued to change at
that rate. (In the circular motion situation, the acceleration is of course
changing all the time. To see why it is sometimes necessary to pick small time
intervals, consider what would happen if the body goes around the circle
completely in one second. Then, if you pick two times one second apart, you would conclude the velocity isn’t changing at all, so there is no acceleration.)
An Accelerating Body that isn't Moving
We've stated before that a ball thrown vertically upwards has
constant downward acceleration of 10 meters per second in each second,
even when it's at the very top and isn't moving at all. The key point here is
that acceleration is rate of change of velocity. You can't tell what the rate
of change of something is unless you know its value at more than one time. For
example, speed on a straight road is rate of change of distance from some given
point. You can't get a speeding ticket just for being at a particular point at
a certain time: the cop has to prove that a short time later you were at a point
well removed from the first point, say, three meters away after one-tenth of a
second. That would establish that your speed was thirty meters per second,
which is illegal in a 55 m.p.h. zone. In just the same way that speed is rate
of change of position, acceleration is rate of change of velocity. Thus to
find acceleration, you need to know velocity at two different times. The ball
thrown vertically upwards does have zero velocity at the top of its path, but
that is only at a single instant of time. One second later it is
dropping at ten meters per second. One millionth of a second after it reached
the top, it is falling at one hundred-thousandth of a meter per second. Both
of these facts correspond to a downward acceleration, or rate of change of
velocity, of 10 meters per second in each second. It would only have zero
acceleration if it stayed at rest at the top for some finite period of time,
so that you could say that its velocity remained the same -- zero -- for, say, a
thousandth of a second, and during that period the rate of change of velocity,
the acceleration, would then of course be zero. Part of the problem is that
the speed is very small near the top, and also that our eyes tend to lock on to a moving object to see it better, so there is the illusion that it comes to rest and stays there, even if not for long.
Galileo's Analysis of Motion: Two Kinds
Galileo's analysis of projectile motion was based on two concepts:
1. Naturally accelerated motion, describing the vertical
component of motion, in which the body picks up speed at a uniform rate.
2. Natural horizontal motion, which is motion at a steady speed in a straight line, and happens to a ball rolling across a smooth table, for example, when frictional forces from surface or air can be ignored.
Newton Puts Them Together
Newton's major breakthrough was to show that these two different kinds of
motion can be thought of as different aspects of the same thing. He did
this by introducing the idea of motion being affected by a force, then
expressing this idea in a quantitative way. Galileo, of course, had been well
aware that motion is affected by external forces. Indeed, his definition of
natural horizontal motion explicitly states that it applies to the situation
where such forces can be neglected. He knew that friction would ultimately
slow the ball down, and -- very important -- a force pushing it from behind would
cause it to accelerate. What he didn't say, though, and Newton did, was that
just as a force would cause acceleration in horizontal motion, the natural
acceleration actually observed in vertical motion must be the result of
a vertical force on the body, without which the natural vertical motion would also be at a constant speed, just like natural horizontal motion. This vertical force is of course just the force of gravity.
Force is the Key
Therefore the point Newton is making is that the essential difference
between Galileo's natural steady speed horizontal motion and the natural
accelerated vertical motion is that vertically, there is always the force of
gravity acting, and without that -- for example far into space -- the natural motion
(that is, with no forces acting) in any direction would be at a steady
speed in a straight line.
(Actually, it took Newton some time to clarify the concept of force, which
had previously been unclear. This is discussed at length in Never at Rest,
by Richard Westfall, and I have summarized some of the points here.
Newton's First Law: no Force, no Change in Motion
To put it in his own words (although actually he wrote it in Latin, this is
from an 1803 translation):
Law 1
Every body perseveres in its state of rest, or of uniform motion in a
right line, unless it is compelled to change that state by forces impressed
thereon.
He immediately adds, tying this in precisely with Galileo's work:
Projectiles persevere in their motions, so far as they are not retarded
by the resistance of the air, or impelled downwards by the force of gravity.
Notice that here "persevere in their motions" must mean in steady speed
straight line motions, because he is adding the gravitational acceleration
on to this.
This is sometimes called "The Law of Inertia": in the absence of an external
force, a body in motion will continue to move at constant speed and direction,
that is, at constant velocity.
So anyacceleration, or change in speed (or direction of motion), of a body signals that it is being acted on by some force.
Newton's Second Law: Acceleration of a Body is Proportional to Force
Newton's next assertion, based on much experiment and observation, is that, for
a given body, the acceleration produced is proportional to the strength of
the external force, so doubling the external force will cause the body to pick
up speed twice as fast.
Law 2
The alteration of motion is ever proportional to the motive force impressed; and is made in the direction of the right line in which that force is impressed.
What About Same Force, Different Bodies?
Another rather obvious point he doesn't bother to make is that for a given force,
such as, for example, the hardest you can push, applied to two different
objects, say a wooden ball and a lead ball of the same size, with the lead ball with the lead ball weighing seven times as much as the wooden ball, then the lead ball will only pick up speed at one-seventh the rate the wooden one will.
Falling Bodies One More Time: What is Mass?
Now let us consider the significance of this law for falling bodies. Neglecting
air resistance, bodies of all masses accelerate downwards at the same rate. This
was Galileo's discovery.
Let us put this well established fact together with Newton's Second Law: the
acceleration is proportional to the external force, but inversely
proportional to the mass of the body the force acts on.
Consider two falling bodies, one having twice the mass of the other.
Since their acceleration is the same, the body having twice the mass must be
experiencing a gravitational force which is twice as strong. Of course, we are
well aware of this, all it's saying is that two bricks weigh twice as much as
one brick. Any weight measuring device, such as a bathroom scales, is just
measuring the force of gravity. However, this proportionality of mass and
weight is not a completely trivial point. Masses can be measured against each
other without using gravity at all, for example far into space, by
comparing their relative accelerations when subject to a standard force, a push.
If one object accelerates at half the rate of another when subject to our
standard push, we conclude it has twice the mass. Thinking of the mass in this
way as a measure of resistance to having velocity changed by an outside force, Newton called it inertia.
(Note that this is a bit different from everyday speech,
where we think of inertia as being displayed by something that stays at rest. For
Newton, steady motion in a straight line is the same as being at rest. That
seems perhaps counterintuitive, but thats because in ordinary life, steady motion in a straight line usually causes some frictional or resistive forces to come into play.)
Mass and Weight
To return to the concept of mass, it is really just a measure of the amount
of stuff. For a uniform material, such as water, or a uniform solid, the
mass is the volume multiplied by the density -- the density being defined as the
mass of a unit of volume, so water, for example, has a density of one gram per
cubic centimeter, or sixty-two pounds per cubic foot.
Hence, from Galileo's discovery of the uniform acceleration of all falling
bodies, we conclude that the weight of a body, which is the amount of stuff it’s made of.
The Unit of Force
All the statements above about force, mass and acceleration are statements
about proportionality. We have said that for a body being accelerated by a
force acting on it the acceleration is proportional to the (total) external
force acting on the body, and, for a given force, inversely proportional to the
mass of the body.
If we denote the force, mass and acceleration by F, m and a
respectively (bearing in mind that really F and a are vectors
pointing in the same direction) we could write this:
F is
proportional to ma
To make any progress in applying Newton's Laws in a real situation, we need
to choose some unit for measuring forces. We have already chosen units for
mass (the kilogram) and acceleration (meters per second per second). The most
natural way to define our unit of force is:
The unit of force is that force which
causes a unit mass (one kilogram) to accelerate with unit acceleration (one
meter per second per second).
This unit of force is named, appropriately, the newton.
If we now agree to measure forces in newtons, the statement of
proportionality above can be written as a simple equation:
F = ma
which is the usual statement of Newton's Second Law.
If a mass is now observed to accelerate, it is a trivial matter to find the
total force acting on it. The force will be in the direction of the
acceleration, and its magnitude will be the product of the mass and
acceleration, measured in newtons. For example, a 3 kilogram falling body, accelerating downwards at 10 meters per second per second, is being acted on by a force ma equal to 30 newtons, which is, of course, its weight.
Newton's Third Law: Action and Reaction
Having established that a force -- the action of another body -- was necessary to
cause a body to change its state of motion, Newton made one further crucial
observation: such forces always arise as a mutual interaction of
two bodies, and the other body also feels the force, but in the opposite
direction.
Law 3
To every action there is always opposed an equal and opposite reaction:
or the mutual actions of two bodies upon each other are always equal, and
directed to contrary parts.
Newton goes on:
Whatever draws or presses another is as much drawn or pressed by that
other. If you press a stone with your finger, the finger is also pressed by
the stone. If a horse draws a stone tied to a rope, the horse (if I may so
say) will be equally drawn back towards the stone: for the distended rope, by
the same endeavour to relax or unbend itself, will draw the horse as much
towards the stone, as it does the stone towards the horse, and will obstruct
the progress of the one as much as it advances that of the other. If a body
impinge upon another, and by its force change the motion of the other, that
body also (because of the equality of the mutual pressure) will undergo an
equal change, in its own motion, towards the contrary part. The changes made
by these actions are equal, not in the velocities but in the motions of bodies;
that is to say, if the bodies are not hindered by any other impediments. For,
because the motions are equally changed, the changes of the velocities made
towards contrary parts are reciprocally proportional to the bodies. This law
takes place also in attractions.
All this maybe sounds kind of obvious. Anyone who's had a dog on a leash,
especially a big dog, is well aware that tension in a rope pulls both ways. If
you push against a wall, the wall is pushing you back. If that's difficult to
visualize, imagine what would happen if the wall suddenly evaporated. Newton's insight here, his realization that every acting force has a reacting force, and
that acceleration of a body only occurs when an external force acts on it, was one of the big forward steps in our understanding of how the Universe works.
Newton's Second Law in Everyday Life
The Second Law states that if a body is accelerating, there must be an
external force acting on it. It's not always obvious what this external force
is even in the most trivial everyday occurrences. Suppose you're standing
still, then begin to walk. What was the external force that ca's very hard to
start walking if you're wearing smooth-bottomed shoes and standing on smooth
ice. You tend to skid around in the same place. If you understand that, you
also know what external force operates when a car accelerates.
The reason the external force causing the acceleration may not be
immediately evident is that it may not be what's doing the work. Consider the
following scenario: you are standing on level ground, on rollerskates, facing a
wall with your palms pressed against it. You push against the wall, and roll
away backwards. You accelerated. Clearly, you did the work that caused the
acceleration. But from Newton's second law, your acceleration was, in fact,
caused by the reactive external force of the wall pushing your hands, and hence
the rest of you. That is to say, the force causing the acceleration may not be
generated directly by what -- or who -- is doing the work! In this example, it's
generated indirectly, as a reaction force to that of the hands pushing on the
wall. But if the wall were on wheels, and it accelerated away when you pushed
(having taken off your roller skates) the force causing the acceleration of the
wall would be generated directly by the agent doing the work, you.
Now imagine two people on roller skates, standing close facing each other,
palms raised and pushing the other person away. According to Newton's
discussion above following his Third Law, the two bodies involved will undergo
equal changes of motion, but to contrary parts, that is, in opposite directions.
That sounds reasonable. They obviously both move off backwards. Notice,
however, that Newton makes a special point of the fact that these equal (but
opposite) "motions" do not imply equal (but opposite) velocities: this becomes
obvious when you imagine the experiment with a 100 pound person and a 200 pound
person. Newton tells us that in that situation the heavier person will roll
backwards at half the speed: notice he says the velocities are "reciprocally
proportional to the bodies".
Roller skates actually provide a pretty good example of the necessity of
generating an external force if you want to accelerate. If you keep the skates
pointing strictly forwards, and only the wheels are in contact with the ground,
it's difficult to get going. The way you start is to turn the skates some, so
that there is some sideways push on the wheels. Since the wheels can't turn
sideways, you are thus able to push against the ground, and therefore it is
pushing you: you've managed to generate the necessary external force to
accelerate you. Note that if the wheels were to be replaced by ball bearings
somehow, you wouldn't get anywhere, unless you provided some other way for the ground to push you, such as a ski pole, or maybe twisting your foot so that some fixed part of the skate contacted the ground.
Gravity
We have now reached the last sentence in Newton's discussion of his Third
Law: This law also takes place in attractions. This of course is
central to Newton's (and our) view of the Universe. If the Earth is attracting
the Moon gravitationally with a certain force holding it in its orbit, then the
Moon is attracting the Earth with an equal force. So why isn't the Earth going
around the Moon? The answer is that the masses are so different. The Earth's
mass is more than one hundred times that of the Moon. Consequently, the
Earth's acceleration, "falling" towards the Moon, is very small. What actually
happens is that they both circle around a balance point between them, which in
fact lies within the Earth. This motion of the Earth is easily detectable with
instruments, but tiny compared with the daily rotation. Of course, it also
follows from the above considerations that since the Earth is attracting you downwards with a force equal to your weight, you are attracting the Earth upwards—towards you—with a force of exactly the same strength.
The Law of Gravity
Let us now put together what we know about the gravitational force:
1. The gravitational force on a body (its weight, at the Earth's surface)
is proportional to its mass.
2. If a body A attracts a body B with a gravitational force
of a given strength, then B attracts A with a force of equal
strength in the opposite direction.
3. The gravitational attraction between two bodies decreases with distance,
being proportional to the inverse square of the distance between them. That
is, if the distance is doubled, the gravitational attraction falls to a quarter
of what it was.
One interesting point here: think about how the Earth is gravitationally
attracting you. Actually, all the different parts of the Earth are attracting
you! Mount Everest is pulling you one way, the Antarctic ice mass a different
way, and the Earth's core is pulling you downwards. Newton managed to prove,
after thinking about it for years, that if the Earth is a sphere (which is a
very good approximation) then all these different attractions add up to what
you would feel if all the Earth's mass were concentrated in one point
at the center. So, when we're talking about the gravitational attraction
between you and the Earth, and we talk about the distance of separation, we
mean the distance between you and the center of the Earth, which is just
less than four thousand miles (6300 kilometers).
Let's denote the gravitational attractive force between two bodies A
and B (as mentioned in item 2 above) by F. The forces on the two
bodies are really equal and opposite vectors, each pointing to the other body,
so our letter F means the length of these vectors, the strength
of the force of attraction.
Now, item 1 tells us that the gravitational attraction between the Earth and
a mass m is proportional to m. This is an immediate consequence
of the experimental fact that falling bodies accelerate at the same rate,
usually written g (approximately 10 meters per second per second), and
the definition of force from Newton's Second Law above. Thus we have
F is
proportional to mass m
for the Earth's gravitational attraction on a body (often written weight W
= mg), and Newton generalized this finding to assert that this
proportionality to mass would be true for any gravitational attraction
on the body.
From the symmetry of the force (item 2 above) and the proportionality to the
mass (item 1), it follows that the gravitational force between two bodies must
be proportional to both masses. So, if we double both masses, say, the
gravitational attraction between them increases by a factor of four. We see
that if the force is proportional to both masses, let's call them M and m,
it is actually proportional to the product Mm of the masses. From
item 3 above, the force is also proportional to 1/r2, where r
is the distance between the bodies, so for the gravitational attractive force
between two bodies
F is
proportional to Mm/r2
This must mean that by measuring the gravitational force on something, we
should be able to figure out the mass of the Earth! But there's a catch: all we
know is that the force is proportional to the Earth's mass. From that
we could find, for instance, the ratio of the mass of the Earth to the mass of
Jupiter, by comparing how fast the Moon is falling around the Earth to how
fast Jupiter's moons are falling around Jupiter. For that matter, we could
find the ratio of the Earth's mass to the Sun's mass by seeing how fast the planets
swing around the Sun. Still, knowing all these ratios doesn't tell us the
Earth's mass in tons. It does tell us that if we find that out, we can then find the masses of the other planets, at least those that have moons, and the mass of the Sun.
Weighing the Earth
So how do we measure the mass of the Earth? The only way is to compare the
Earth's gravitational attraction with that of something we already know the
mass of. We don't know the masses of any of the heavenly bodies. What this
really means is that we have to take a known mass, such as a lead ball, and
measure how strongly it attracts a smaller lead ball, say, and compare that
force with the Earth's attraction for the smaller lead ball. This is very
difficult to accomplish because the forces are so small, but it was done
successfully in 1798, just over a century after Newton's work, by Cavendish.
In other words, Cavendish took two lead weights M and m, a few
kilograms each, and actually detected the tiny gravitational attraction
between them (of order of magnitude millionths of a newton)! This was a
sufficiently tough experiment that even now, two hundred years later, it's not
easy to give a lecture demonstration of the effect.
Making this measurement amounts to finding the constant of proportionality
in the statement about F above, so that we can sharpen it up from a
statement about proportionality to an actual useable equation,
F = GMm/r2
where the constant G is what Cavendish measured, and found to be 6.67
x 10-11 in the appropriate units, where the masses are in kilograms,
the distance in meters and the force in newtons. (Notice here that we can't
get rid of the constant of proportionality G, as we did in the equation F
= ma, Newton's Second Law, above. We succeeded there by defining the
unit of force appropriately. In the present case, we have already defined our
units of mass, distance and force, so we have no further room to maneuver.)
From Newton's theory of universal gravitational attraction, the same
constant G determines the gravitational attraction between any two
masses in the universe. This means we can now find the mass of the
Earth. We just consider a one kilogram mass at the Earth's surface. We
know it feels a force of approximately 10 newtons, and is a distance of about
6300 km, or 6,300,000 meters, from the center of the Earth. So we know every
term in the above equation except the mass of the Earth, and therefore
can find it. This is left as an exercise.
previous
index
next
PDF
