How Astronomy Developed: Early Lunar Observations and some Planetary Models
Eclipse of the Moon

The ancient Greeks watched this closely, and from it estimated the distance to the Moon within 10%.
Ptolemy's Successful Model for the Inner Planets
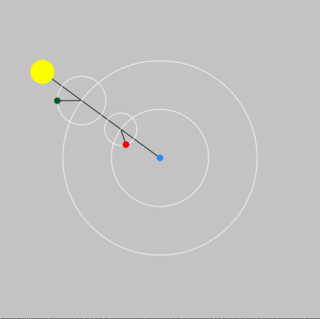
A system of cycles and epicycles accounted well for the observed motions of Venus and Mercury.
Ptolemy's Successful Model for the Motions of Mars and Jupiter
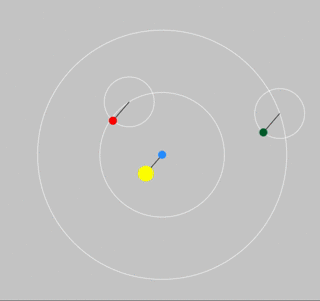
A system of cycles and epicycles accounted well for the observed motions of Mars and Jupiter.
The Tusi Couple
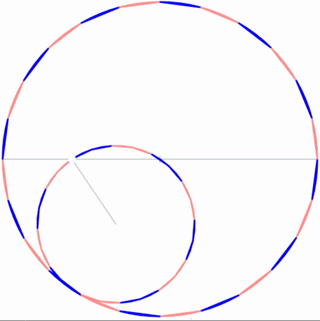
A refinement to Ptolemy’s epicycles to account for a small linear oscillation, but made from circular motions.
Ptolemy v Copernicus
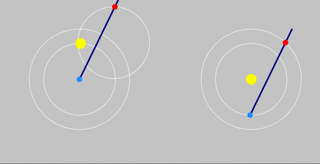
Demonstrating why observing the path of Mars through the Heavens cannot settle the argument.
The Inner Planets

Relative orbital sizes and periods of the inner planets: Mercury, Venus, Earth and Mars.
The Outer Planets

Relative orbital sizes and periods of the outer planets: Jupiter, Saturn, Uranus and Neptune.
Platonic Solids: Kepler's idea
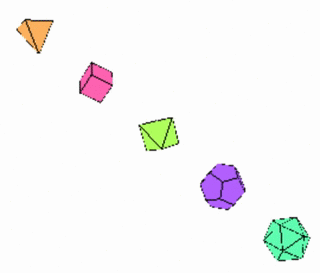
Kepler theorized that the planets moved on spherical surfaces separated by having Platonic solids just fit between neighboring orbits: see his model here.
Kepler's Laws

Set a planet in motion, and watch Kepler's Third Law in action.
Phases of Venus

This applet shows Venus' orbit from different perspectives to understand how the sunlit half of the planet exhibits phasess like the Moon.
How Galileo and Newton Invented Dynamics
Projectile Motion as Compound Motion
Animating Galileo’s own diagram combining steady horizontal motion and constant vertical acceleration to give a parabolic trajectory.
Projectile Motion
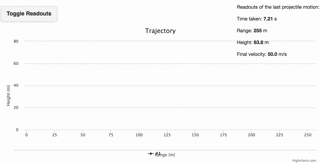
A very accurate applet, plotting multiple trajectories, and including realistic air resistance.
Newton's Mountain
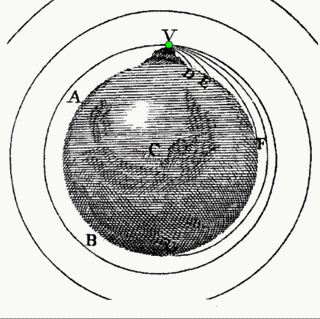
Newton’s realization that the parabolic motion of a cannonball and the circular motion of the Moon were different aspects of the same thing, that the Heavens and the Earth obeyed the same laws, was the key scientific contribution to the Enlightenment.
Newton's Analysis of Circular Acceleration
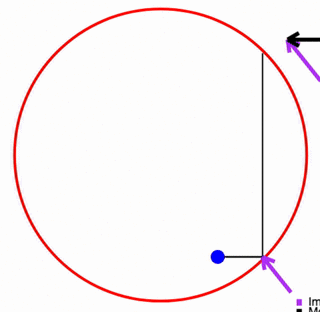
He began with motion round a regular polygon, with impulses at the corners to change direction, then increasing side numbers to approach a circle. This is essentially how calculus evolved.
Planning a Trip to Mars
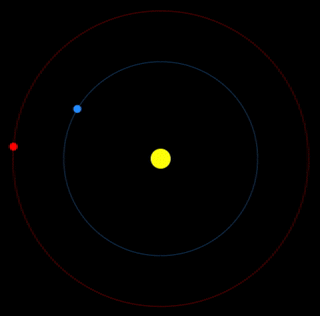
Try finding a successful launch strategy: what speed and at what orbital time to land on Mars?
General Planetary Orbits
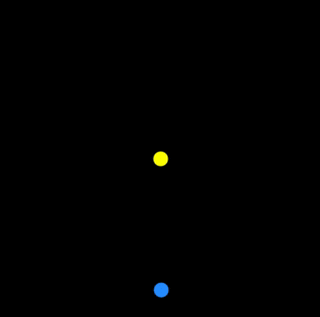
What if the attraction were not inverse square? (It isn’t in General Relativity). And, when are orbits stable?
Relativity and Nuclear Physics
The Michelson-Morley Experiment
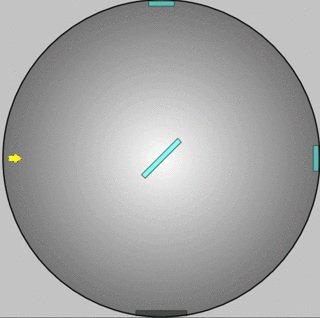
Once it was clear that light is a wave, what was waving? Light could move through a vacuum (from the Sun and stars). It was assumed that a material called aether must fill all space, and waves as light passed through. This experiment was designed to detect it.
Time Dilation from a Lightclock

A clock based on bouncing light between two mirrors shows why the constancy of light speed means all moving clocks run slow.
Two Dimensional Collisions
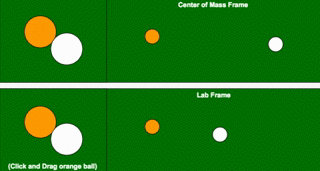
Simple 2D elastic collisions, viewed in the lab frame and the CM frame: a relativistic version makes inertial mass increase with speed understandable.
Rutherford Scattering

Rutherford scattered heavy energetic charged particles (“alphas”) from gold atoms to try to find how the positive charge was spread through the atom—the accepted Thomson AtomThomson model had it fairly evenly distributed. To his amazement, he discovered the observed scattering could only be explained by the presence of a very tiny nucleus containing essentially all the mass and charge.
Nuclear Chain Reaction

Press Start to see the grid of nuclei, then press for one nucleus to emit a neutron. If that hits another nucleus, two new neutrons come out. There is almost certainly runaway reaction for a big enough grid: above the “critical size”.
Oscillations and Waves
Simple Harmonic Motion is a Shadow
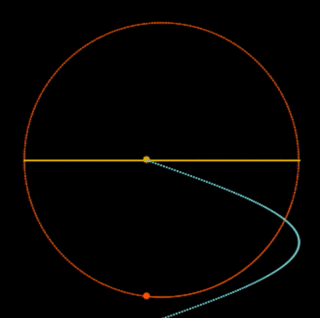
Simple harmonic motion is the shadow on a diameter of steady circular motion.
Vibrating String and Newton’s Laws

The wave equation follows from F = ma for a tiny bit of string.
Visualizing a Sound Wave

A traveling sound wave carries energy, but this applet shows there is no net movement of the air, despite appearances.
Reflection of a Wave Pulse at a Boundary

Inverted for a fixed end, not for a free end: this can be understood by watching two pulses collide.
Wave Pulse Encounters a Different Medium
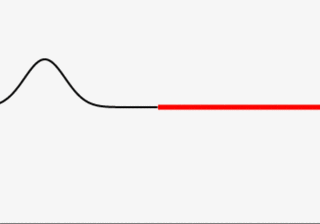
Here a change in string density, but the same result as light going from air to glass, for instance.
Doppler Effect

Observe the change in frequency of sound (or light!) from a moving source.
Two-Slit Wave Interference Pattern

Synchronized waves from two slits have constructive/destructive interference at points with relative slit distances same phase/opposite phase.
Building the Two Slit Pattern on a Screen

Checking the relative phase from the slits at each point on a screen to construct the interference pattern.
Group Velocity and Phase Velocity
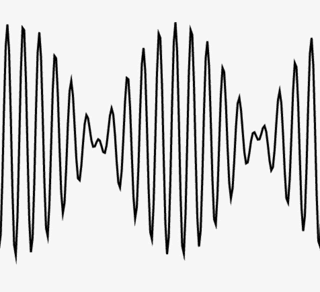
How do they relate? Is one always bigger? Find the answer with this simple applet.
Simply Adding Two Moving Sine Waves
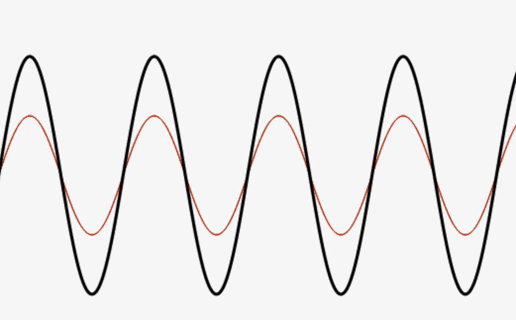
The results can be surprising!
Statistical Mechanics and Thermodynamics
One-dimensional one-atom classical gas

The temperature of a gas is proportional to the kinetic energy of the molecules. Watch how compression heats things up!
Carnot Cycle

This animation correlates the basic Carnot engine cycle to the corresponding P,V graph plus a thermometer.
Einstein's Explanation of Brownian Motion

This applet shows how molecular velocities cause the Brownian Motion of a dust particle. Through the microscope, a tiny particle jitters. With (difficult to achieve!) further magnification we see it's because energetic molecules are pummeling it.
Diffusion
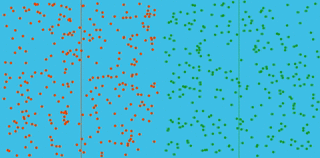
A box has red particles in the left hand half, green in the right. They all begin with the same speed but random direction. Watch as they mix! How long will it take? The vertical lines give the average positions of red and green particles.
Try different numbers of particles and different sizes
Maxwell Molecular Speed Distribution
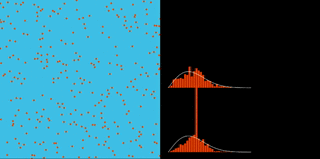
Beginning with all molecular speeds equal, the dynamics rapidly evolves to the theoretical speed distribution predicted by Maxwell (with the predicted size-dependent fluctuations).
Exponential Atmosphere: Dynamics + Gravity

Adding gravity to colliding molecules dynamics leads to exponential density drop off with height, but uniform temperature.
Dynamics of Viscous Flow
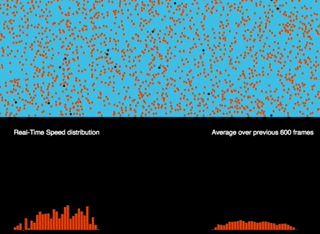
A dynamic realization: initially equal speeds, and constant gravity along the pipe. Bouncing off the walls, they lose their along the pipe velocity component. The velocity along the pipe approaches a parabolic profile.
Some Simple Mathematics
The Platonic Solids

The only three-dimensional flat faced solids with every face identical, and every vertex identical.
Cycloid

The path traced by a point on a wheel as the wheel rolls on a flat surface.
Hypocycloids
The path traced by a point on a wheel as the wheel rolls inside a circle.
Damped Driven Oscillators
Heavy Damping: Pendulum in Molasses

A system with two time scales: discover the physics with this applet.
Critical Damping: A Bumpy Road

Is this the ideal damping for good shocks?
Damped Driven Oscillator: Response to Initial Conditions
Plotting together the responses of the oscillator to different initial values, the curves can look completely different, but their difference is simple.
Damped Driven Oscillator

Investigate how a damped simple harmonic oscillator responds to being externally driven at different freequencies: in particular, near resonance.
Phase Lag Change near Resonance in Driven Oscillator

The phase lag is the key to the power transfer rate. Here you can investigate how it varies with driving frequency and damping.
Particle in Anharmonic Potential

See the motion of a particle in a simple harmonic oscillator potential with adjustable cubic and quartic terms added.
Driven Damped Oscillator with added Quartic Term
Near resonance, gradually increasing the driving frequency increases the amplitude—until there is a discontinuous drop!
Damped Driven Pendulum: The Road to Chaos
Damped Driven Pendulum: Period Doubling and Chaos
Explore how gradually increasing the driving force leads to a cascade of period doublings, then to chaos.

Damped Driven Pendulum II: Sensitivity to Initial Conditions
In nonchaotic parameter regimes, small initial differences die away; in chaotic regimes they explode. Explore the transition.
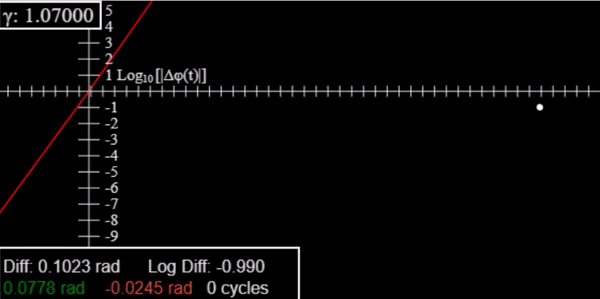
Damped Driven Pendulum III: Lyapunov
In chaos, initially close trajectories diverge exponentially, the Lyapunov exponent quantifies this. Here you can set initial conditions and actually measure the exponent.

Damped Driven Pendulum IV: State Space
Plotting the motion in 2D (position and velocity), gives new insight into period doubling, stability and chaos.
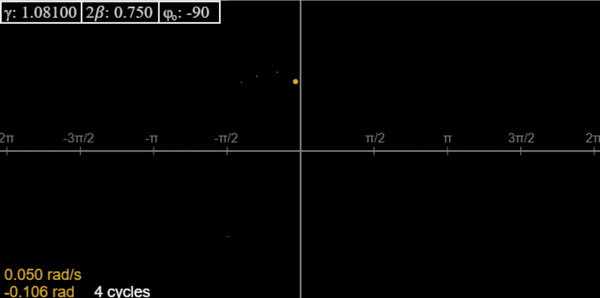
Damped Driven Pendulum V: Poincaré Section and Strange Attractors
Taking snapshots of the 2D motion one cycle apart gives a few dots in the non-chaotic regime (after initial transients), but for chaos an amazing fractal pattern can emerge—a strange attractor. You can watch it develop with this applet.