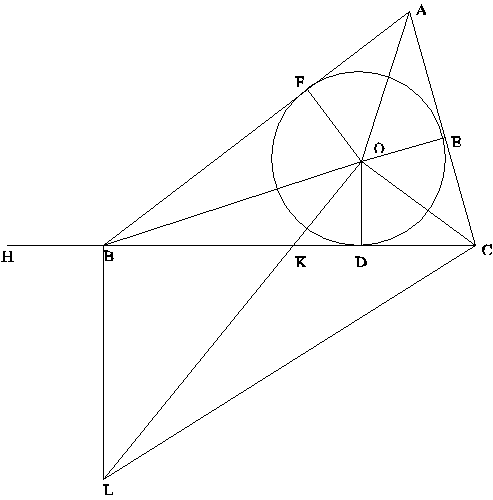
Geometrical Proof of Heronís Formula
(From Heathís History of Greek Mathematics, Volume2)
Area of a triangle = sqrt[s(s-a)(s-b)(s-c)], where s = (a+b+c)/2
The triangle is ABC. Draw the inscribed circle, touching the sides at D, E and F, and having its center at O.
Since OD = OE = OF, area ABC = area AOB + area BOC + area COA,
2.area ABC = p.OD, where p = a+b+c. (a = (length of) BC, etc.)
Extend CB to H, so that BH = AF. Then CH = p/2 = s. (since BD = BF, etc.)
Thus (area ABC)2 = CH2.OD2.
Draw OL at right angles to OC cutting BC in K, and BL at right angles to BC meeting OL in L. Join CL.
Then, since each of the angles COL, CBL is right, COBL is a quadrilateral in a circle.
Therefore, angle COB + angle CLB = 180 degrees.
But angle COB + angle AOF = 180 degrees, because AO bisects angle FOE, etc., so
Angle AOF = angle CLB
Therefore, the right-angled triangles AOF, CLB are similar, and
BC:BL = AF:FO = BH:OD
CB:BH = BL:OD = BK:KD
And from CB/BH = BK/KD, adding one to each side, CH/HB = BD/DK, or
CH:HB = BD:DK
It follows that
CH2:CH.HB = BD.DC:CD.DK = BD.DC:OD2 (since angle COK = 90 degrees)
Therefore (area ABC)2 = CH2.OD2 = CH.HB.BD.DC = s(s-a)(s-b)(s-c).
According to Heath, this proof is really due to Archimedes. It should be mentioned that it is of course a lot easier to prove the result using trigonometry! The area of a triangle is 1/2ab.sinC, and using c2=a2+b2-2ab.cosC, and sin2+cos2=1, the result follows in a few lines.
I think the following argument also constitutes a proof: consider the square of the area of a triangle of sides a, b, c. Dimensionally, it must be a homogeneous expression of fourth degree (a quartic) in a, b, c. It must also be symmetric in a, b, c (it can't matter which sides of a given triangle are labelled with which letters), and the area of the triangle must be zero if the length of any one of the sides equals the sum of the other two, -- so a+b-c must be a factor, etc. This gives Heron's expression, except for an overall multiplicative factor which can be determined by taking an easy example, such as a triangle of sides 1, 1, sqrt2. (Obviously, there is no quadratic expression in a, b, c satisfying our requirements, so we are forced to consider the square of the area rather than the area itself.)