Brownian Motion

Michael Fowler, U. Va.

See Applet here!

Introduction: Jiggling Pollen Granules

In 1827 Robert Brown, a well-known botanist, was studying sexual relations of plants, and in particular was interested in the particles contained in grains of pollen. He began with a plant (Clarkia pulchella) in which he found the pollen grains were filled with oblong granules about 5 microns long. He noticed that these granules were in constant motion, and satisfied himself that this motion was not caused by currents in the fluid or evaporation. Smaller spherical grains, which at first he took to be oblongs end-on, but later realized weren’t, had even more vigorous motion. He thought at first that he was looking at the plant equivalent of sperm $—$ they were jiggling around because they were alive. To check this, he did the same experiment with dead plants. There was just as much jiggling. Perhaps all organic matter, everything that ever was alive, still contained some mysterious life force at this microscopic level? Sure enough, he found the movement in tiny fragments of fossilized wood! But then he went on to find it in matter that never was alive $—$ tiny particles of window glass, and even dust from a stone that had been part of the Sphinx. The movement evidently had nothing to do with the substance ever being alive or dead, much to Brown’s surprise. So what was causing it? Perhaps it was evaporation currents, or the incident light energy, or just tiny unnoticed vibrations. But none of these explanations was very satisfactory.

Half a century later, a new possible explanation emerged. The kinetic theory of heat developed by Maxwell, Boltzmann and others was gaining credence. If all the molecules in the fluid were indeed in vigorous motion, maybe these tiny granules were being moved around by this constant battering from all sides as the fluid molecules bounced off. But there was a problem with this explanation: didn’t it violate the second law of thermodynamics? It had been well established that energy always degrades, as friction slows movement kinetic energy goes to heat energy. This seemed to be the other way round $—$ the molecular battering was certainly disorganized heat energy, but when the granule moved it had evidently gained kinetic energy. Since many scientists regarded the second law as an absolute truth, they were very skeptical of this explanation.

In 1888, French experimentalist Léon Gouy investigated the movement in detail, finding it to be more lively in low viscosity liquids. He established that it was unaffected by intense illumination or by strong electromagnetic fields. Despite the second law, Guoy believed $—$ correctly $—$ the random motion was indeed generated by thermal molecular collisions.

It’s easy to see the Brownian movement, or Brownian motion (it’s called both) by looking through a microscope at tobacco smoke in air. There's a movie here.

Einstein’s Theory: the Osmosis Analogy

In 1905, Einstein published a theoretical analysis of Brownian motion. He saw it as a crucial test of the kinetic theory, even of the atomic/molecular nature of matter. Previous discussions of the phenomenon had all been qualitative $—$ Einstein demonstrated that careful observation of Brownian motion could reveal the actual size of molecules, that is, find Avogadro’s number.

If the results of such experiments were consistent with other estimates of Avogadro’s number, based on unrelated phenomena such as gas viscosity measurements and van der Waal’s equation fit to isotherms of real gases, it would be a powerful argument for the kinetic theory. On the other hand, if there was real disagreement then the kinetic theory was in serious trouble.

Einstein’s approach was based on an analogy with osmosis: recall that osmosis involves one substance (the solute) dissolved in another, the solvent. The solute has larger molecules. Now imagine a container divided in two by a semipermeable membrane, meaning the solvent molecules can pass through the tiny holes in it, but the solute molecules are too big to get through. Suppose on one side of the membrane there’s pure solvent, on the other side solvent plus solute (assumed fairly dilute), and initially the pressure on the two sides of the membrane is the same. The pressure on the side with solute is generated by both solvent and solute molecules bouncing off the membrane, so necessarily the rate at which solvent molecules are hitting the membrane on this side is less than on the other side. Some percentage of the solvent molecules hitting the membrane pass through the little holes, so what will happen is that more will pass through from the pure solvent side, and gradually pressure will build up on the solvent + solute side until equilibrium is reached, meaning equal numbers of solvent molecules going each way on average.

Einstein’s insight was that a liquid containing a large number of tiny identical particles, such as those observed in Brownian motion, was really no different from a solvent containing solute molecules. True, the Brownian particles were a lot bigger than molecules, but they were buzzing around, and would therefore bounce off the walls of a container, generating pressure. The formal analysis should be the same: the kinetic theory, with equipartition of energy, predicted they would have kinetic energy 1.5k_BT. If the concentration of particles varied spatially, they would flow to even it out.

Here again he used an osmosis analogy: think of a cylindrical container, with a semipermeable membrane which is like a piston, free to move. The solute concentration is initially greater to the left of the piston.

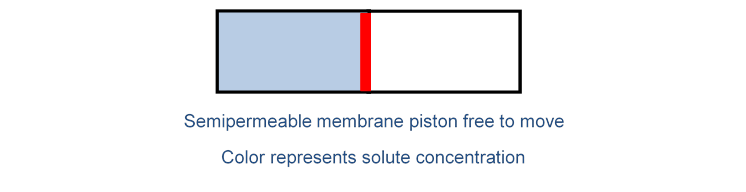
From the previous discussion, it’s clear that the solvent will flow to the left, raising the pressure there, so the piston will move to the right. The solute molecules cannot cross the piston, so the piston will move until the solute concentrations on the two sides are equal.

The rather surprising result is that if one assumes equipartition of energy, the pressure on the piston from the solute on one side is the same as if those solute molecules were freely moving in a vacuum.

Their greatly reduced mean free path doesn’t matter: the pressure depends only on the concentration in the immediate neighborhood of the piston, and the speed of the molecules. And, this is equally true if the solute molecules are replaced by tiny but macroscopic spheres. At least, this is what Einstein asserted, and he gave a formal proof based on an evaluation of the free energy, assuming a dilute system (meaning interactions between the spherical granules could be neglected).

So we can think of the little spheres as moving freely through space (!), and although their paths will actually be very different, calculations of local pressure based on this should be correct: the pressure on the walls from the granules is therefore given by the ideal gas law, that is,

$P = \frac{1}{3} m n \bar{v^{2}} = \frac{2}{3} n \bar{\frac{1}{2} m v^{2}} = \frac{2}{3} n \bar{K . E .} = \frac{2}{3} n W$

where the average kinetic energy is written $W,$ and $—$ if the kinetic theory is correct $—$ this should equal $1.5 k_{B} T .$ Of course, this is just the same as for a gas, but the big difference is that these particles are big enough to see, so we can find the density $n$ just by counting! So if we can measure the pressure generated by these particles, we can find $W$ and therefore Boltzmann's constant.

An Atmosphere of Yellow Spheres

So how is this to be done experimentally? As we shall see in a moment, the first experiment used uniformly sized tiny spheres in place of granules. The first obvious thought is that if $\bar{\frac{1}{2} m v^{2}}$ is predicted to be $1.5 k_{B} T,$ perhaps one can just measure the jiggling velocity of the tiny sphere a few times and take an average. This, however, misunderstands the nature of the motion: a molecule will bounce off the sphere around 10²⁰times per second, and although that only makes a tiny difference to the sphere’s velocity, in one hundredth of a second the average imbalance, $\sqrt{N},$ will be of order 10⁹, enough to make a change in a small sphere’s velocity. And all the successive changes are completely random in direction, so it’s as hopeless as attempting to measure the velocity of H₂S molecules in air by releasing a few and measuring the time for the smell to reach the far end of a room.

A slightly less direct method of finding $\bar{\frac{1}{2} m v^{2}}$ is needed. Now, it is well-known that in an isothermal atmosphere of an ideal gas under gravity the density falls off exponentially with height, this is established by balancing the gravitational force on a thin horizontal slice against the pressure difference between top and bottom. (Note: if you don't recall this, see my lecture here.) It occurred to the French experimentalist Jean Perrin that this same argument should apply to a “gas” of tiny uniform spheres in a fluid: their pressure is effectively generated by the Brownian motion. In 1908, he chose gamboge, an emulsion used for water color, which contains bright yellow spheres of various sizes. By various ingenious tricks described in his book he was able to separate out spheres all close to the same size. He was able to measure the size, he knew the density $—$ and that of the “solvent” $—$ so he could compute the gravitational pull. He could also measure the decrease in density with height in isothermal equilibrium.

The calculation is as follows: for a horizontal slice of unit area and thickness $d h,$ with $n$ spheres per unit volume, each of volume $φ$ and density $Δ,$ in a liquid of density $δ$ (I’m using Perrin’s notation here), the gravitational downward force on the slice is $n d h φ (Δ - δ),$ this is balanced by the pressure difference:

$- Δ P = - \frac{2}{3} W d n = n d h φ (Δ - δ) .$

This is easily integrated to give the exponential vertical density profile.

$\frac{d n}{d h} = - \frac{n φ (Δ - δ)}{\frac{2}{3} W}, n (h) = n (0) \exp (- \frac{φ (Δ - δ)}{\frac{2}{3} W} h) .$

Perrin could establish by observation and measurement every term in this equation except $W,$ so this was a way of measuring $W,$ assuming of course the validity of the kinetic theory.

Now equating $W$ to $1.5 k_{B} T$ gives a value for Boltzmann’s constant, and hence via the known gas constant $R = N_{A} k_{B},$ a value for Avogadro’s number.

Perrin repeated the experiment with a wide variety of different substances, the experiments were very challenging, his results for Avogadro’s number were consistently between 5×10²³ and 8×10²³. He remarked that for the largest granules behaving like a perfect gas, a gram molecule would weigh 200,000 tons! The results were consistent with the other quite different ways of finding Avogadro’s number, and these experiments convinced even the most recalcitrant anti-atomic theory skeptics. The kinetic theory was fully established.

Langevin’s Theory

In 1908, Langevin gave a more direct treatment of Brownian motion. He focused on following one particle as it jiggled around. We’ll follow him in restricting the motion to one dimension $—$ assuming the molecular collisions driving the motion are completely random, the motions in the three directions are uncorrelated, so can be treated separately and added. Finally, we’ll neglect gravity and any other external force fields.

Let’s assume, then, that we’re tracking a small spherical object, of mass $m$ and radius $a .$ It will experience a viscous drag force $- 6 π a η v$ (Stokes’ formula). We’ll denote the random thermal molecular collision force by $X,$ which clearly averages to zero.

Assuming the equipartition of energy applies also to the kinetic energy of our sphere (and remember we're working in one dimension only),

$\bar{m {(\frac{d x}{d t})}^{2}} = k_{B} T$

where the average is over a long time.

The equation of motion $m a = F$ is:

$m \frac{d^{2} x}{d t^{2}} = - 6 π a η \frac{d x}{d t} + X .$

To integrate this equation, we begin by multiplying throughout by $x :$

$m x \frac{d^{2} x}{d t^{2}} = - 6 π a η x \frac{d x}{d t} + X x$

which can be written

$m \frac{d}{d t} (x \frac{d x}{d t}) - m {(\frac{d x}{d t})}^{2} = - 3 π a η \frac{d}{d t} x^{2} + X x .$

To eliminate the unknown random force, we average over a long time:

$m \bar{\frac{d}{d t} (x \frac{d x}{d t})} - m \bar{{(\frac{d x}{d t})}^{2}} = - 3 π a η \bar{\frac{d}{d t} x^{2}} + \bar{X x} .$

Since $X$ is random, $\bar{X x} = 0.$ Also, $m \bar{{(d x / d t)}^{2}} = k_{B} T,$ and $x (d x / d t) = \frac{1}{2} d (x^{2}) / d t .$

The operations of averaging and taking the time derivative commute, so we can write the equation:

$\frac{m}{2} \frac{d^{2}}{d t^{2}} \bar{x^{2}} + 3 π a η \frac{d}{d t} \bar{x^{2}} = k_{B} T .$

The trick to solving this equation is to write $\frac{d}{d t} \bar{x^{2}} = y,$

So the equation becomes:

$\frac{d y}{d t} + \frac{6 π a η}{m} y = \frac{2 k_{B} T}{m},$

with solution:

$y (t) = \frac{k_{B} T}{3 π a η} + C \exp (- \frac{6 π a η}{m} t) .$

For the actual systems examined experimentally, the exponential term dies off in far less than a microsecond, so for a particle beginning at the origin:

$\frac{d}{d t} \bar{x^{2}} (t) = y (t) = \frac{k_{B} T}{3 π a η},$

therefore

$\bar{x^{2}} (t) = \frac{k_{B} T}{3 π a η} t .$

Hence by doing multiple experiments and averaging, Boltzmann’s constant $k_{B}$ can be found, and from that Avogadro’s number, as before.

Note that the constancy of $(d / d t) \bar{x^{2}} (t)$ also appears in discussions of random molecular motion and the random path $—$ this is all the same thing.

Exercises:

Estimate the decay time of the exponential term in the integrated expression for $y (t)$ above. You’ll need to find the viscosity of water, and estimate the sphere size as a few microns.
Estimate how rapidly density of yellow spheres drops with height in Perrin’s “atmosphere”.
Notice the average distance traveled in the last equation above depends on the kinetic energy, the size, and the viscosity. This means a tiny lead sphere would diffuse the same distance, on average, as a tiny sphere of oil of the same size. But isn’t the lead moving a lot more slowly, since it has the same average kinetic energy? Explain.

Reference Books

For Brown’s work, see A Source Book in Physics, W. F. Magie, Harvard, 1963, page 251, where several pages from the original pamphlet are reproduced.

Albert Einstein: Investigations on the Theory of the Brownian Movement, Dover, New York, 1956.

Jean Perrin: Brownian Motion and Molecular Reality, Dover, New York, 2005.

Langevin’s paper in translation: Am. J. Phys. 65 (11), November 1997, 1079.

Wolfgang Pauli: Pauli lectures on Physics Volume 4, Statistical Mechanics. Dover, New York, 2000, page 64.

previous index next